一种人口迁移行为的动力学模拟与结构熵分析

郝睿，宋佳，霍杰，王旭明

(1.宁夏大学 物理电气信息学院，宁夏 银川 750021； 2.宁夏沙漠信息智能感知重点实验室，宁夏 银川 750021)

人类行为的复杂性源于人对事件进行判断和决策的复杂性.人作为社会系统中的个体，其行为总会与其他个体行为发生或多或少的联系，并最终影响系统的发展进程和结果.2005年Barabási发表在《Nature》上的文章揭示出人类行为的时间规律具有高度的非均匀性，即长时沉默，短时频发[1].该工作开创了复杂网络新的研究方向——人类动力学.目前，人类动力学研究已经向多元化方向发展，相关研究不仅揭示了诸多人类行为发生的时间规律，而且展示了人类行为的空间规律[2-6].上述研究多是关于个体行为的动力学，或是基于个体的爱好或兴趣决定的群体行为动力学[7-8]，对人类出行距离分布规律的研究也仅限于对大量个体行为的统计[9-10].然而，还有一类人类社会行为的发生会受到自然因素的制约和限制，这些在利益驱动下做出的群体决策行为所展示的规律值得深入研究.人类动力学的发展为探讨群体行为提供了新的研究视角.本文基于网络思想和人口迁移动力学特征，并结合迁移“推拉”理论[11]，研究特定自然因素影响下的农业人口迁移行为，为此，提出了一个能够反映群体迁移现象的动力学模型.模型中重点考虑了人类在利益驱动下所做出的迁移选择，并考察了迁移行为对系统结构熵的影响.

1 模型的建立

影响人口迁移的因素有很多，如自然因素、社会因素、情感及政治因素.中国为农业国，本文将首先重点考察农业人口的迁移.不同区域由于农业产值、气候条件、人口密度不同，会引发人口迁移.迁移欲望发生时，迁移者会受到来自外界的拉力和内在的推力作用.拉力表现为迁入区高的人均收入、良好的人居环境等，推力则表现为迁出地的人均低收入水平.考虑到迁移现象的空间关联性，迁移距离对迁移成本的影响也将被考虑，为此，建立一个网格模型，网格中的每一节点代表一个区域，区域间的距离将由两点之间的距离等效替代.某区域在某一时期的人均收入可等效为人均粮食产量，而人均粮食产量则由区域人口、亩产量、耕地面积决定.将时间离散化为每一收获期并定义为时步，则某区域在某时步的人均粮食产量为

(1)

式中i=1,2,…，N，N为区域总数.g(ii1,i2,j)为第i个区域第j时步的人均粮食产量，下角标i1,i2代表第i个区域的格点位置坐标；C(ii1,i2,j)，q(ii1,i2,j)和R(ii1,i2,j)分别代表该区域总的耕地面积、亩产量和人口数.该时期所有区域的总体人均粮食产量Aver_g(j)为

(2)

不同地区的人均粮食产量与总体人均值之间的差距为迁移提供可能性.当迁入区农业经济水平达到或超过迁出地可能移动人口的预期目标时，迁移行为发生.依据不同地区的人均粮食产量，可将不同区域划分为迁入区和迁出区.自然的，也会存在人口暂时不发生迁移的区域，这些区域的人口变化方程为

R(ii1,i2,j+1)=R(ii1,i2,j).

(3)

对迁出区，本地亩产量的变化趋势若呈上升趋势，则人口的迁移欲望会受到抑制，反之，人口迁移欲望加强.在同一时期，农业经济发达的地方越多，为迁移人口提供的迁入区域就越多，导致迁出区人口的迁移欲望加强.此外，某迁出区人均粮食产量与系统总体人均粮食产量差别越大，说明该地区农业经济发展水平越低，该区域人口的迁移愿望越强烈.为在系统中体现不同迁出区群体迁移需求的强弱，每一迁出区人口迁移意愿受经济发展水平制约的权重表现为，总体人均粮食产量与该区域人均粮食产量的差值占所有迁出区域该差值总和的比例.综合上述3种因素，某迁出区的迁移人口数量与迁入地个数，更低的亩产量和更大的农业经济差距正相关，相应的迁移人口表达式为

(4)

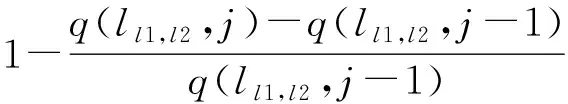
R(ll1,l2,j+1)=R(ll1,l2,j)-R_out(ll1,l2,j),l=1,2,…，M2.

(5)

迁出人口在不同迁入地吸引力的影响下会做出迁入地选择.这里，将重点考虑迁入地农业经济发展水平及迁移距离的影响.若第j时步有M1个迁入地，则其中第k个迁入地人均粮食产量与总体平均值差值越大，说明该区域农业经济水平越发达，则该区域对迁出人口越具吸引力.同时，该迁入地与同一迁出地的距离越远，意味着迁移成本越高，则该地对迁出人口的吸引力受到抑制.相应的第k个迁入地在第j时步的迁入人口数为R_in(kk1,k2,j)为

(6)

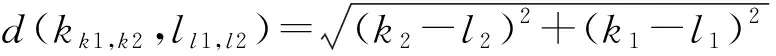
(7)

实际生产中，受经济发展水平，气候条件等多方面影响，每一区域的亩产量会有所浮动，相应的方程为

q(i,j+1)=q(i,j)·[1+k(i,j+1)].

(8)

式(8)中k(i,j+1)为影响亩产量涨落的相关因子，可在一定数值范围内随机产生，以模拟实际生产中的随机涨落.至此，由式(1)―(8)共同构成了受耕地面积制约的人口迁移模型.

2 模拟结果

在给定每个区域亩产量、人口数量及耕地亩数的前提下，依据判断标准可将所有区域进行迁出和迁入地的界定，按照上述演化规则，不同区域间将发生人口迁移，迁移量会引起区域人口数发生新的变化.同时，区域亩产量的随机浮动也将进一步促使区域人均粮食产量发生变化，新的变化将引发新的人口迁移.人口迁移行为的结束将取决于每一区域人口不再发生变化.模拟时，取C(i,j)=C(i,0)=rand(3.33～8)×104hm2，rand表示随机数；R(i,0)=rand(20～60)万人；q(i,0)=rand(150～500)kg；k(i,j)=rand(-0.1～0.1).为反映人口的迁移期望，模拟过程中，某地人均粮食产量高于总体人均值1.1倍的区域为迁入区；低于总体人均值0.9倍的区域为迁出区；位于两者之间的是暂时不发生人口迁移的地区.通过模拟，某迁出地人口及人均粮食产量随时步的变化趋势如图1及图2所示，图中结果表明，迁出区人口随时步呈递减趋势，随着人口的减少，该区域人均粮食产量上升，区域人口迁移强度将会逐渐降低，最终使得该区域人口不再发生迁移，并且人口和人均粮食产量曲线的变化是同步的.图2中的宽带平台表示人均产量受亩产量随机浮动虽然会有涨落，但这种涨落已经不能促使迁移行为发生.图3及图4反映了某迁入区人口及人均粮食产量随时步的变化趋势.结果表明，迁入区人口随着时间的推移逐渐增加，同时，人均粮食产量呈减小趋势.图3中前半段人口的迁入起主导作用，所以图4中人均粮食产量出现了陡降；图4后半段表示人均粮食产量的自然涨落已不能构成新的吸引力，所以对应该段的人口也将保持不变.这也可以理解为该区域已经发展到了农业人口与耕地相对平衡的阶段.

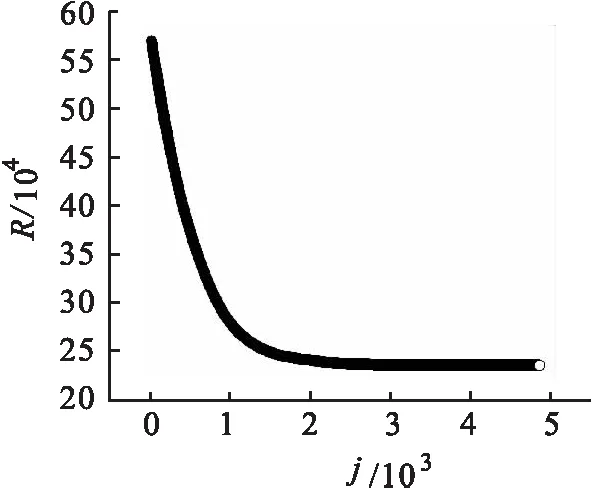
图1 迁出区人口随时步的变化趋势 Fig.1 Changing trends of population with time-steps in emigration area

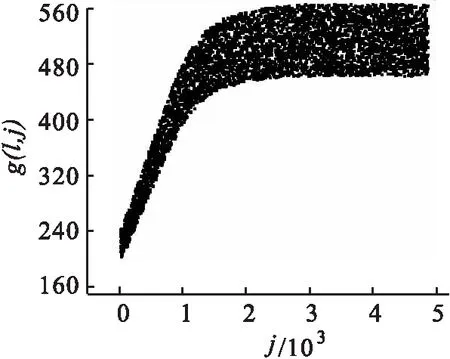
图2 迁出区人均粮食产量随时步的变化趋势 Fig.2 Changing trends of food production per captia with time-steps in emigration area

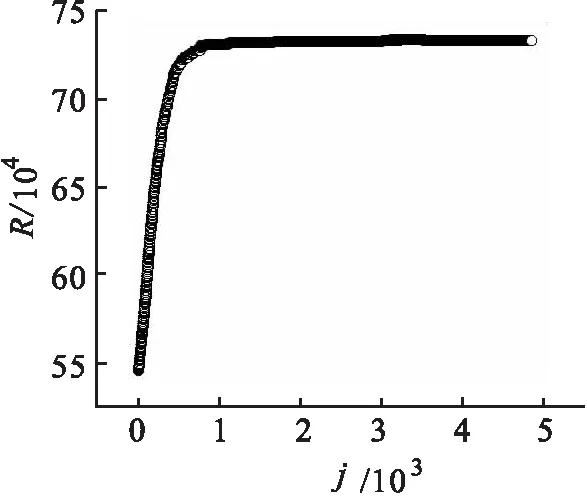
图3 迁入区人口随时步的变化趋势 Fig.3 Changing trends of population with time-steps in immigration area

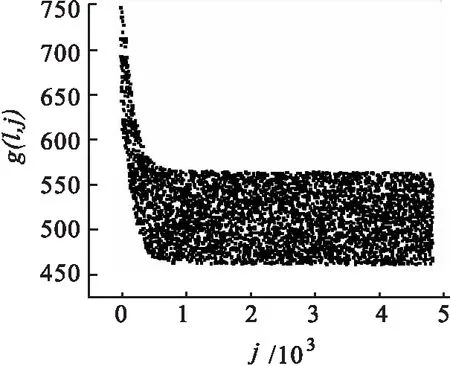
图4 迁入区人均粮食产量随时步的变化趋势 Fig.4 Changing trends of food production per captiawith time-steps in immigration area

(9)

图5 人口结构信息熵随时步的变化趋势 Fig.5 Changing trends of structure entropy with time-steps

式(9)中H(j)为每一时步的人口结构信息熵.上述迁移过程中人口结构信息熵随时间的变化趋势如图5所示.图5中结果表明，熵值出现了先增后减的趋势，峰值出现的时步为j=454.这说明，人们最初的迁移是发生在对外界信息还不能充分掌握的背景下，此时迁移的目的性并不强，迁移行为的发生相对混乱，迁移行为发生的频率较高，系统人口结构变化的无序度较强，熵值较大.随着迁移行为的持续发生，人们对外界信息的掌握越来越全面，迁移行为会更理性，目的性会更强，系统内的迁移行为也越有序.相应的，系统人口结构变化趋势将从无序向有序过渡，并逐步走向平衡，熵值随之降低.为进一步显示这一进程中，各个区域人口规模的变化，本文给出了不同时步人口规模斑图，如图6所示，人口规模大小分别为深灰色(高于53.2万)，浅灰色(26.6万～53.2万)和黑色(低于26.6万).图6a给出了j=0时人口规模的最初分布.受外部环境刺激，人们开始向经济水平相对发达的地区迁移，导致更多区域人口规模变大，如图6b所示，深灰及浅灰色区域明显增多.这一过程与熵图中上升的部分相对应.此后，随着人们对外界信息量掌握的越来越全面，迁移行为更加理性，人口规模较小的黑色区域数量开始回升，而规模较大的深灰、浅灰色区域数量有所回落，直至人口不再发生移动，相应的结果如图6c及6d所示.这一变化与熵减过程相对应.熵值之所以从某一时步(本文中是第454步)开始回落，可能正是因为起初人们的盲目迁移造成很多区域，特别是农业经济水平发展居中的浅灰色区域容纳了更多的人口，在耕地面积有限的前提下，超负荷的农业人口有可能制约当地的农业经济发展水平.当迁入地不能使迁移人口受益时，势必会引起人口的理性回迁，其结果相当于给系统输入了负熵，从而引起熵值减小.熵值减小的过程也许正是人口结构变化理性回归的一种体现.

深灰色； 浅灰色； 黑色图6 不同时步下的人口规模斑图 Fig.6 Population size patterns on different time-steps

3 结论

影响人口迁移的因素主要可分为自然因素和社会因素.本文结合网络思想，重点考察了自然因素影响下的农业人口迁移行为，并建立了相应的动力学模型.模型中人口迁移行为的发生既会受到来自迁入地的“拉力”效应，也会受到迁出地的“推力”作用.迁移环境中既考虑了耕地面积不变的确定项，也包含了亩产量涨落的随机项.模拟结果表明最初的迁移往往具有盲目性，即无序迁移发生的概率相对较高，此时，系统的人口结构信息熵呈增加趋势.在无序迁移发展进程中，随着人们对信息的掌握越来越全面，目的明确的有序迁移开始发生，系统的人口结构信息熵随之减小.

受耕地面积制约的农业人口迁移反映了自然因素影响下的一种人类群体决策行为.研究其动力学过程将为揭示诸多此类现象(如生态移民、草原牧民转场等)提供借鉴和启示.自然变化和人类利益取向间的反馈作用机制也许正是人类群体决策行为发生的根源所在.研究组不仅对自然因素影响下的群体决策行为进行了分析，还讨论了社会因素对人口迁移的作用机制，相关结论将另文报道.

参 考 文 献:

[1] BARABáSI A-L. The origin of bursts and heavy tails in human dynamics[J]. Nature，2005，435：207-211.

[2] NI Shunjiang，WENG Wenguo. Impact of travel patterns on epidemic dynamics in heterogeneous spatial metapopulation networks [J]. Physical Review E，2009，79(1)：016111.

[3] MIN B，GOH K-I，KIM I-M. Waiting time dynamics of priority-queue networks[J]. Physical Review E，2009，79(5)：056110.

[4] 汪秉宏，韩筱璞. 人类行为的动力学与统计力学研究[J]. 物理，2010，39( 1)：28-37.

WANG Binghong，HAN Xiaopu. The dynamics and statistical mechanics of human behaviors[J]. Physics，2010，39(1)：28-37.

[5] CANDIA J，GONZáLEZ M C，WANG P，et al. Uncovering individual and collective human dynamics from mobile phone records[J]. Physica A，2008，41(22)：224015.

[6] KAN A，CHAN J，HAYES C，et al. A time decoupling approach for studying forum dynamics[J]. World Wide Web，2012(1)：1-27.

[7] 任学藻，杨紫陌，汪秉宏. 演化网络的Mandelbrot律[J].电子科技大学学报，2011，40(2)：163-167.

REN Xuezao，YANG Zimo，WANG Binghong. Mandelbrot law of evolution networks[J]. Journal of University of Electronic Science and Technology of China，2011，40(2)：163-167.

[8] WANG Peng，XIE Xiaoyi，YEUNG C-H，et al. Heterogenous scaling in the inter-event time of on-line bookmarking[J]. Physica A，2011，390(12)：2395-2400.

[9] GONZáLEZ M C，HIDALGO C A，BARABáSI A-L. Understanding individual human mobility patterns[J]. Nature，2008，453(7196)：779-782.

[10] JIANG Bin, YIN Junjun, ZHAO Sijian. Characterizing the human mobility pattern in a large street network[J]. Physical Review E，2009，80(2)：021136.

[11] LEE E S. A theory of migration [J]. Demography，1966，3(1 )：47-57.

[12] 曾忠平，裴韬，彭兰霞. 武汉南湖湖区土地利用结构信息熵与湖泊形态变化分形分析[J].资源科学，2008，30(7)：1061-1067.

ZENG Zhongping，PEI Tao，PENG Lanxia. Fractal analysis and information entropy of land use structure for lake morphology in urban lake area Wuhan city[J]. Resources Science，2008，30(7)：1061-1067.

[13] 耿红，唐旭，马玲. 基于信息熵的城市土地利用结构合理性分析[J]. 国土资源科技管理，2006，23(1)：84-87.

GENG Hong，TANG Xu，MA Ling. Rationality analysis of urban land use structure based on shannon entropy[J]. Scientific and Technological Management of Land and Resources，2006，23(1)：84-87.