介观电子谐振腔的量子化

刘志成，阎占元 ，马金英

(1.华北电力大学 科技学院，河北 保定 071003；2. 华北电力大学 数理学院，河北 保定 071003)

随着微电子学和纳米技术的飞速发展，集成电路的基本设备尺度已经到达介观层次，其量子效应不可忽视，介观电路的量子理论应运而生[1].Louisell在20世纪70年代，最早进行了介观LC电路的量子化，借用简谐振子的量子化方法，得到了真空态下体系的量子涨落[2].之后的近20年的时间里，对介观电路的研究几乎没有进展，到了20世纪90年代中期，随着电路越来越小型化，介观电路量子理论的越来越急需.人们从不同的角度先后研究了介观LC电路、介观RLC电路以及介观耦合电路分别处于不同的某些特定状态下的量子力学效应，得到了一些具有一定意义的结果[3-9].在量子化介观电路时，关键的是把电路合适量子化，然后求解系统的薛定谔方程.方法大致分为3类：1)借用简谐振子的量子化方法，或引入产生和湮灭算符实现介观电路量子化[2,10]，这是目前研究最为广泛和深入的一种方法.2)在电荷分立取值的基础上，重新定义广义坐标动量算符和哈密顿算符，建立一种有限差分形式的薛定谔方程，实现介观电路的量子化[5,11]，对有限差分形式薛定谔方程的求解困难，限制了这类方法的应用范围.3)在路径积分的基础，求解出系统的传播子，从而得到系统的性质[12-13].

介观电子谐振腔是一种介观器件[14]，近年来，因其电阻振荡性引起了人们的广泛关注[15].本文采用Feynman路径积分的方法对介观电子谐振腔进行了量子化.应用高斯型传播子，求出系统的能级，得到波函数随时间的演化公式，进而讨论系统的量子涨落和不确定关系.

1 介观电子谐振腔的量子化

图1 介观电子谐振腔示意 Fig.1 Sketch drawing of the mesoscopic electron resonator

按照Utreras Diaz等人[16]的模型，介观谐振腔结构如图1所示，是由1个量子点接触和1个圆弧形反射壁组成，反射壁上电压为Vg.电子通过量子点接触注入系统，在空腔内多次反射，从反射壁的两侧流出.系统等效为LC电路.

系统的经典哈密顿为

(1)

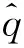
(2)

2 系统传播子

在路径积分形式中，只要确定系统的传播子，任意时刻的波函数可通过初态演化而得.传播子的泛函积分形式为

(3)

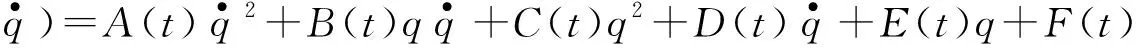
(4)

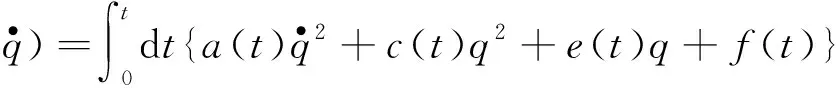
(5)

(6)

其中Scl为经典作用量，与δq无关.过程用到δq在端点为零和运动方程.路径积分的测度变成D[q(t)]=D[δq(t)]，传播子化为

(7)

其中A(t)是对δq积分后的结果.所以二次型的作用量，对应的传播子是高斯型.为计算简便，写出以下一般形式的高斯型传播子，再定出各项系数.

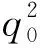
(8)

传播子满足薛定谔方程

(9)

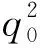
(10)

(11)

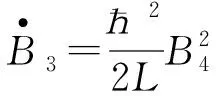
(12)

(13)

(14)

(15)

解以上微分方程，并利用初始条件K(q,t;q0,0)

t→0=δ(q-q0)，可得6个系数分别为

(16)

(17)

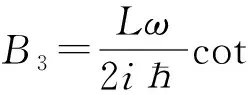
(18)

(19)

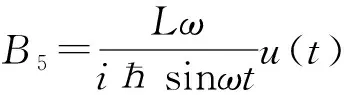
(20)

(21)

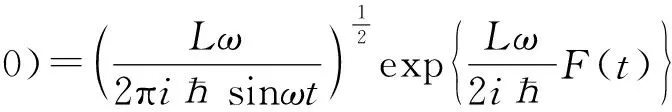
(22)

其中

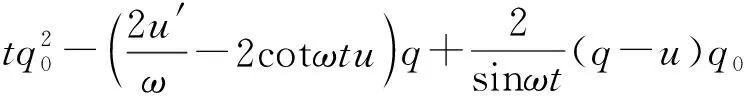
(23)

3 系统波函数

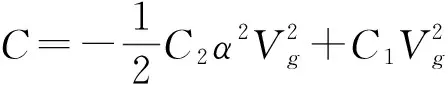
(24)

令t=0，可得系统的初态波函数和能级：

(25)

(26)

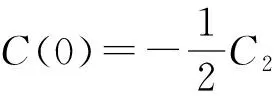
应用传播子式(22),容易得到体系任意时刻的波函数，

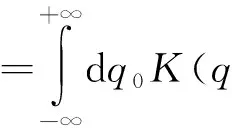
(27)

即

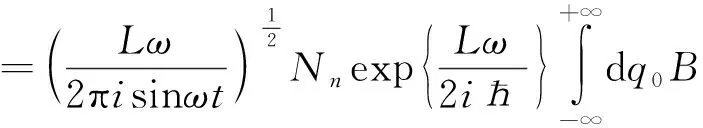
(28)

其中，

(29)

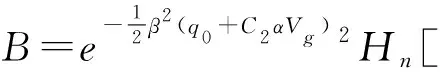
(30)

利用恒等式

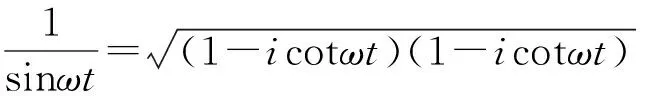
(31)

(32)

(33)

化简得到体系任意时刻波函数为

(34)

其中γ=cosωtC2αVg+q-u.

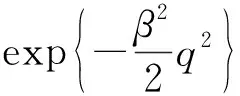
4 量子涨落和不确定关系

作为以上得到的波函数的应用，利用上节结论和厄密多项式的性质，可求解体系的量子涨落和不确定关系.

(35)

(36)

(37)

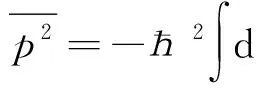
(38)

因此，涨落为

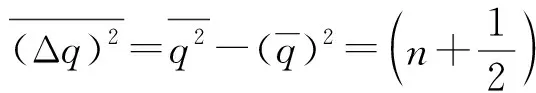
(39)

(40)

.

(41)

5 结论

本文在介观电子谐振腔等效电路的哈密顿基础上，采用Feynman路径积分的方法对介观电子谐振腔进行了量子化求解.应用高斯型传播子，求出了系统的能级以及波函数随时间的演化公式，并讨论了系统的量子涨落和不确定关系.结果表明，无耗散的介观电子谐振腔系统的电荷和电流的量子涨落，与介观LC电路的量子涨落相同，并且不随时间变化.

参 考 文 献:

[1] BUOT F A. Mesoscopic physics and nanoelectronics[J]. Phys Rep, 1993, 234:73-174.

[2] LOUISELL W H. Quantum statistical properties of radiation[M]. New York：John Wiley,1973．

[3] LI Youquan，CHEN Bin．Quantum theory for mesoscopic electric circuits[J]．Phys Rev，1996，B(53)：4027-4032.

[4] ZHANG Zhiming, HE Lisheng, ZHOU Shikang. A quantum theory of an RLC circuit with a source[J].Phys Lett,1998,A244(4):196-200.

[5] WANG Jisuo，SU Changyong. Quantum effects of mesoscopic RLC circuit in squeezed vacuum state[J].Int J Theor Phys,1998,37(4):1213-1216.

[6] FAN Hongyi, LIANG Xianting. Quantum fluctuation in thermal vacuum state for mesoscopic LC electric circuit[J].Chin Phys Lett,2000,17(3):174-176.

[7] LEI Minsheng,JI Yinghua,Xie Fangsen. Quantum squeezing effects of a non-dissipative mesoscopic circuit with coupled inductors and capacitors[J].Chin Phys Lett，2001,18(2):163-165.

[8] SUN Changpu. Quantum dynamical model for wave-function reduction in classical and mesoscopic limits[J].Phys Rev,1993,A48(2):898-906

[9] BENJAMIN C, JAYANNAVAR A M. Current magnification effect in mesoscopic systems at equilibrium[J].Phys Rev, 2001,B64:233406-233410.

[10] 陈斌，高守恩，焦正宽．低温下介观电路的量子涨落[J]．物理学报，1995，44(9)：1480-1483．

CHEN Bin,GAO Shouen, JIAO Zhengkuan.Quantun fluctuation of mesoscopic circuit at low temperatures[J]. Acta Phisics Sinica, 1995，44(9)：1480-1483．

[11] YAN Zhanyuan, ZHANG Xiaohong, HAN Yinghui. Quantum Effect in mesoscopic open electron resonator[J].Commun Theor Phys,2008,50(2):521-524.

[12] 凌瑞良，吴娟花.RLC介观电路的量子化研究[J].大学物理,2009,28(11):3-5.

LING Ruiliang, WU Juanhua. On the quantum mechanical treatment of a RLC mesoscopic circuit[J]. College Physics, 2009, 28(11):3-5.

[13] JI Yinghua,LUO Haimei,LEI Minsheng. The squeezing effect in a mesoscopic RLC circuit[J]. Commun Theor Phys,2002,38(11):611-614.

[14] KATINE A,ERIKSON M A, ADOURIAN A S,et al. Point contact conductance of an open resonator[J].Phys Rev Lett,1997,79:4806-4809.

[15] DUNCAN D S, TOPINKA M A, WEATERVELK R M,et al. Aharonov-Bohm phase shift in an open electron resonator[J].Phys Rev,2001,B64:033310-033314.

[16] UTRERAS-DíAZ C A, FLORES J C, PéREZ-PONCE A. Simple approach to the mesoscopic open electron resonator:Quantum current oscillations[J].Solid State Communications,2005,133(2):93-96.