基于直觉模糊集和有效测度的Choquet积分

杨兰珍 ， 哈明虎，张自儒

(1.河北大学 数学与计算机学院，河北 保定 071002；2.河北软件职业技术学院 学生处，河北 保定 071000)

自模糊集[1]诞生之后，由于其在各领域的广泛应用而引起了大量学者的研究兴趣,这也使模糊集理论得到了大量的推广,直觉模糊集就是其中之一.自从1983年Atanassov 等人[2-3]提出直觉模糊集的概念之后,许多学者也投入到对直觉模糊集的研究工作中，至今直觉模糊集已应用于直觉模糊专家系统、直觉模糊神经网络和群决策、模糊优化、医疗疹断和模糊识别领域.

2009年，Witold等[4-6]提出了基于经典集合的有效测度(或称效率测度)，其实质为一特殊广义模糊集值测度[7]，且其应用主要借助于模糊积分这一工具.然而模糊积分作为整合算子一直备受关注，特别是Choquet积分.此积分是法国学者Choquet于1954年针对容度定义提出的，且作为一种经典的非线性积分，已经被成功应用于信息融合和数据挖掘等领域[8].

值得关注的是，最近有学者纷纷开始研究基于直觉模糊集的Choquet积分[9-12],但是其工作侧重于基于直觉模糊值映射或者基于直觉模糊值测度的Choquet积分.基于此，本文首先将基于经典集合的有效测度推广到基于直觉模糊集合的有效测度，并分析其性质；然后讨论定义在直觉模糊集合上基于实值有效测度和实值可测映射的Chouquet积分，并研究其性质.

设X是一个非空集合, F是由X的若干经典子集组成的σ-代数, (X，F)称为可测空间, C是由X的若干经典子集组成的类.M={f:X→[-∞,∞]|f是可测的}，M+={f:X→[0,∞]|f是可测的}.

定义1[4-6]映射μ: C→[0, ∞] 称为有效测度当且仅当若∅∈C，有μ(∅)=0.

值得关注的是：模糊测度、λ-模糊测度、拟测度、信任测度、似然测度等都是特殊的有效测度.

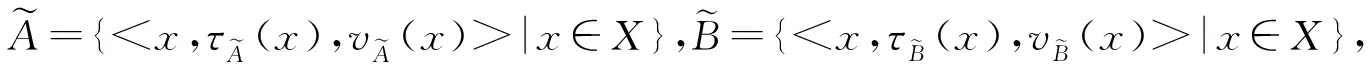
1 基于直觉模糊集的有效测度

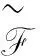
事实上，直觉模糊熵可以认为是一种定义在直觉模糊集上的有效测度.此外，进一步改进直觉模糊特殊测度[13]，给出定义7.

(FM1)平凡性：μ(∅)=0;

注：μ称为下半(或上半)连续实值直觉模糊测度, 如果它满足上述条件(FM1)，(FM2)和(FM3)(或(FM1)，(FM2)和(FM4))；μ称为实值直觉单调测度，如果它满足上述条件 (FM1)和(FM2). 显然，实值直觉模糊测度，半连续实值直觉模糊测度，以及实值直觉单调测度都为特殊的实值直觉有效测度.

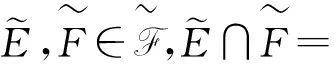
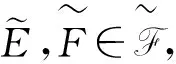
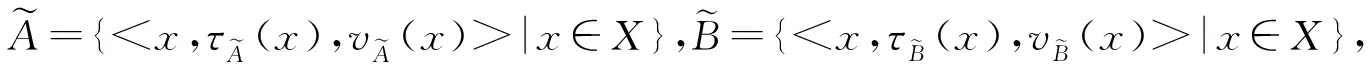
从而根据μ的crisp零可减定义, 有

从而

故μ是crisp零可减的.

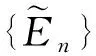
2 基于直觉模糊集和有效测度的Choquet积分

注：命题1中的积分是定义在直觉模糊集上的关于直觉实值有效测度的Choquet积分.

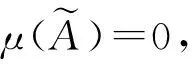
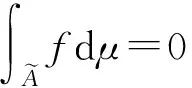
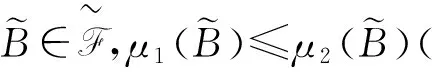
证明类似于一般Choquet积分的证明,故略.

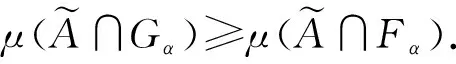
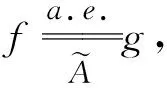
与假设相矛盾.

3 结论

给出了一种基于直觉模糊集的实值有效测度，讨论了crisp零可减，直觉模糊相乘等相关性质；结合有效测度，讨论了直觉模糊集合上的Choquet积分的基本性质，从而推广了基于普通集合和直觉模糊集合的非可加测度论.

参 考 文 献:

[1] ZADEH L A. Fuzzy sets [J].Information and control, 1965, 8: 338-353.

[2] ATANASSOV K. Intuitionistic fuzzy sets[Z].Seventh Scientific Session of ITKR, Sofia, 1983.

[3] ATANASSOV K. Intuitionistic fuzzy sets [J].Fuzzy Sets and Systems, 1986, 20:87-96.

[4] WANG Zhenyuan, LEE K, LEUNG K. The Choquet integral with respect to fuzzy-valued signed efficiency measures[Z].Proc WCCI 2008, Honkong,2143-2148

[5] WANG Zhenyuan,YANG Rong, LEUNG K S. Nonlinear integrals and their applications in data mining[M].Singapore: World Scientific Publishing, 2010.

[6] PEDRYCZ W, YANG Lanzhen, HA Minghu. On the fundamental convergence in the (C) mean in problems of information fusion[J].J Math Anal Appl, 2009, 358: 203-222

[7] 哈明虎，杨兰珍，吴从炘.广义模糊集值测度引论[M].北京：科学出版社，2009.

[8] CHOQUET G. Theory of capacities [J].Annales de l’institut Fourier, 1955, 5: 131-295.

[9] BAN A. Intuitionistic fuzzy measures:Theory and Applieations [M].NewYork: Nova Sciences, 2006.

[10] BAN A, FECHETE I. Componentwise decomposition of some lattice-valued fuzzy integrals [J].Information Science, 2007, 177:1430-1440.

[11] CUI Licong, LI Yongming, ZHANG Xiaohong. Intuitionistic fuzzy linguistic quantifiers based on intuitionistic fuzzy-valued fuzzy measures and integrals[J].International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2009,17:427-448.

[12] 李璐.直觉模糊Choquet积分在语言量词模型中的应用[D].西安：陕西师范大学，2011.

[13] COSKUM E.Syslems on intuitionistic fuzzy special sets and intuitionistic fuzzy special measures [J].Informcotion Science,2000,128:105-118.