随机波浪联合分布概率模型
2014-08-15郄禄文张立丹蒋学炼
郄禄文,张立丹,蒋学炼
(1.河北大学 建筑工程学院,河北 保定 071002;2.天津城建大学 土木工程系,天津 300384)
波浪力是防波堤最重要的外部荷载.文献[1]通过规定"波列累积频率"来反映不同类型建筑物上波浪力的作用性质.从表1可看出,因为波列中个别大波很可能造成直立结构的破坏,且修复困难,因此直立结构采用较小累积频率,而波列中个别大波并不能决定斜坡结构的毁坏,且较易修复,故可采用较大累积频率.
文献[1]中也提出了波浪长期分布推演方法,即基于波浪观测或气象图推算得到的波浪数据分波向统计其波高或周期频率,再利用Pearson-III型、对数正态型、极值I型、Weibull型等理论累积频率分布对经验累积频率曲线拟合外延.
但上述方法获得的波高、周期为离散值,无法清晰表征出两者之间内含的物理关系(在一定水深处,波高、周期之间存在波陡的约束),且无法满足风险评估工作中对波浪要素连续型联合概率分布的要求.因此,本文基于文献[2]和[3]的理论对该问题进行探讨,以提供便于概率积分求解的波高、周期、波向联合概率分布函数.

表1 设计波高的累积频率标准

1 波浪气候综合模式
依照NMIMET模式[2]中,首先分波向对波浪实测数据进行统计分析,获得给定波向下的波高与周期的联合概率分布F(H,T)=F(T|H)F(H),然后加入波向要素以获得三者的联合分布F(H,T,D)=F(H,T|D)F(D).由于实际海况的随机三维性,实时观测的波向与相应的波高周期数据往往不匹配,具有很大的波动性,考虑到极值统计针对大浪,其主波向通常与对应风向偏差很小,因此本文采用分风向代替分波向进行统计分析.需要说明的是,本文提到的波浪周期均为平均跨零周期Tz,以下简称周期(T).
1.1 指定波向的波高极值分布
文献[1]建议利用Pearson-III型、对数正态型、极值I型、Weibull型等理论概型拟合经验累积频率曲线以获得波高长期分布.但文献[4]认为真实海况为风浪涌浪并存的混合浪,上述方法存在较大误差,并建议可借助风速-波高参数化模式推导出波高长期分布,如下.
1)风速-波高联合分布密度
f(H,Wr)=f(H|Wr)f(Wr),
(1)
其中,H为波高,Wr为特征风速,f(Wr)为特征风速的概率密度,f(H|Wr)为指定特征风速Wr下波高H的条件概率密度.
公式(1)的建立基于如下前提:
①指定特征风速Wr对应的波高Hr为合成浪(风浪+涌浪),即
(2)
其中,HY代表Wr=0时的平均涌浪波高,a,n为风成浪的波高参数[5].
②给定风速下的波高标准差
(3)
其中,b,c,d为根据实测数据拟合出的参数[5].
③给定风速下的波高条件分布密度为伽马分布,即
(4)

由式(4)得到f(H|Wr)后,根据概率学理论,通过积分即可求得波高的边缘分布
F(H)=∬f(H|Wr)f(Wr)dHdWr.
(5)
2)波高长期概率分布
由公式(5)获得波高边缘分布F(H)后,可引入理论概型进行外延拟合.由于理论概型对波高长期分布影响很大,故应尝试多种概型,择优选用.工程中常用概型如下:
①对数正态分布
(6)
其中,μh和σh分别是lnH的平均值和标准差.
②Weibull分布
(7)
其中,A为位置参数;B为比例尺参数;C为形状参数.
③极值-I型分布
F(H)=exp(-exp(-(H-A)/B)),
(8)
其中,A为位置参数;B为比例尺参数.
④极值-II型分布
(9)
其中,A为位置参数;B为比例尺参数;C为形状参数.
⑤伽马分布(Pearson-III型曲线)
(10)
其中,A为位置参数;B为比例尺参数;C为形状参数.
⑥广义伽马分布
(11)
其中,A为位置参数;B为比例尺参数;C为形状参数,D为指数参数.
外延拟合过程中,适线法、矩法、概率权重矩法、权函数法及模糊数学法等常用参数估计方法存在计算过程复杂、需人为调整等问题.文献[6]所提出的多变量优化数值方法更为简便,拟合结果与传统方法基本吻合.
1.2 波高与周期的联合分布
迄今为止,已有众多学者对波高-周期长期联合分布进行了研究.其中文献[7]基于波高-周期散布资料所提出的5参数对数正态模式较为常用
(12)
其中μh,μt,σh,σt,ρht分别为h=lnH和t=lnT的均值、标准差、相关系数,可通过计算实测样本(H,T)的对数值(lnH,lnT)样本矩得到.
上述模式虽然获得了较好拟合结果[7],但其要求波高及周期均符合对数正态边缘分布却使其使用受到了限制.所以,此处仍以风速-波高参数化模式来描述其联合分布
f(H,T)=f(T|H)f(H).
(13)
与公式(12)相比,公式(13)的优势在于不限定波高的边缘分布概型f(H).
此外,波周期的条件分布概型[4]
(14)
式中,μt|H为在给定波高H时对数周期t=lnT的条件均值;σt|H为给定波高H时t的条件标准差
其中,σT|H和μT|H为给定波高H下的周期条件均值、标准差,其计算式为
其中,μH,μT,σH,σT,ρHT为H,T的总体平均值、总体标准差和总体相关系数.综合上述公式,基于观测数据获得μH,μT,σH,σT,ρHT5个统计参数,结合波高边缘分布F(H)导出波高周期联合分布F(H,T).其中,μH,σH可由波高边缘分布F(H)直接导出,μT,σT,ρHT则可根据文献[4]的回归公式可得

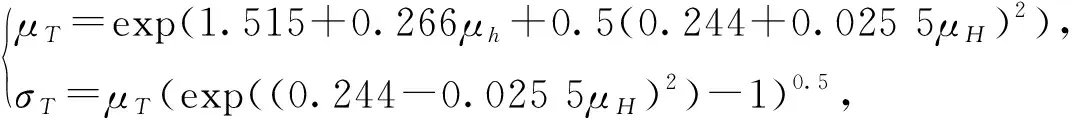
ρHT=0.429+0.095 7σγ,
其中,μt,σt分别为对数周期t=lnT的均值、标准差.波浪受遮蔽的非沿海海域采用上述2种情况的加权值.
1.3 波高-周期-波向联合分布
上述2节给出了指定风向的波高边缘分布F(H)和周期条件分布F(T|H).基于“同时刻主/强波向与主/强风向近似一致”的认识,假定指定波向D与指定风向d条件下的波高-周期的联合概率分布F(H,T)一致,即F(H,T|D,d)≈F(H,T|d),
(15)
基于概率理论,波高-周期-波向的联合分布概型为F(H,T,D)≈F(H,T|d)F(d).
(16)
2 工程实例分析
为验证上述概型的准确性,采用美国国家数据浮标中心(NDBC)46001测站(位于北纬56°17'44"、西经148°10'19",水深为4 206 m,资料跨度为1972—2004年)的实测数据进行日极值系列分析.由于篇幅限制,此处仅列出N向分析结果,其余方向具有类似规律.
利用传统的直接统计方法以及本文提出的多变量函数最小值的数值方法,对46001测站33年波浪(北向)的平均周期和有效波高列于表2和表3,其频数图见图1和图2.

表2 46001测站N向波高-周期联合分布(直接统计)

表3 46001测站N向波高-周期联合分布(本文数值方法)
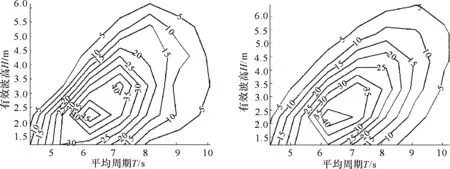
图1 散布频数图(直接统计) 图2 散布频数图(本文方法)Fig.1 Spread frequency chart (Direct statistical method) Fig. 2 Spread frequency chart (Numerical method)
3 结论
本文引入波浪气候综合模式(NMIMET)[2]对波浪观测资料进行统计分析,引进随机波浪多变量联合分布函数,提出一种描述波高、周期、波向联合分布的概型,便于防波堤风险分析与管理过程中的概率积分求解.通过美国国家数据浮标中心46001测站波浪观测数据分析表明,采用求取多变量函数最小值的数值方法进行求解,与传统方法波浪年极值数据拟合结果基本吻合,可有效重现波浪条件,但计算过程更为简便.
参 考 文 献:
[1] 中交第一航务工程勘察设计院有限公司.海港水文规范(JTS 145-2-2013)[M].北京:人民交通出版社,2013.
[2] HOGBEN N, DACUNHA N, ANDREWS K. Assessment of a new global capability for wave climate synthesis[Z]. San Francisco,Proc OCEANS’83, 1983.
[3] 方钟圣.《西北太平洋波浪统计集》与其他图册资料的比较[J].中国海洋平台,1997,12(1):29-32.
FANG Zhongsheng. A comparison of wave data from “wave statistics for Northwest Pacific Ocean Areas” and other Sources[J]. China offshore Platform, 1997,12(1):29-32.
[4] 方钟圣,金承仪,缪泉明.西北太平洋波浪统计集[M].北京:国防工业出版社,1996.
FANG Zhongsheng, JIN Chengyi,MIAO Quanming. Wave statistics for Northwest Pacific Ocean Areas[M].Beijing: National Defence Industrial Press, 1996
[5] 方钟圣,金承仪,缪泉明.中国海与西北太平洋波浪长期统计的导算方法[J].中国造船,1994(4):21-35.
FANG Zhongsheng, JIN Chengyi,MIAO Quanming. On derivation of wave statistics for China seas and northwest Pacific ocean[J].Shipbuilding of China, 1994,4:21-35.
[6] LAGARIAS J C, REEDS J A, WRIGHT M H, et al. Convergence properties of the Nelder-Mead simplex method in low dimensions [J]. SIAM Journal of Optimization, 1998, 9(1): 112-147.
[7] OCHI M K. Wave statistics for the design of ships and ocean structures [J].Trans SNAME, 1978, 86: 47-76.
[8] 方钟圣,戴顺孙,金承仪.海洋特征波高和周期的长期联合分布及其应用[J].海洋学报,1989,11(5):535-543.
FANG Zhongsheng, DAI Shunsun,JIN Chengyi. Long-term joint distribution and application of the ocean wave height characteristics and wave period[J].Acta Oceanologica Sincia, 1989,11(5):535-543.
