改进的三角高程法在跨海高程传递中的应用

徐亚明，施 斌，王代雄，潘正风

(1. 武汉大学 测绘学院，湖北 武汉 430079； 2. 精密工程与工业测量国家测绘地理信息局重点实验室，湖北 武汉 430079)

一、引 言

跨海高程传递是建立国家统一的陆海高程基准框架网的一种重要手段。目前，跨海高程传递的方法通常有三角高程测量法、短期验潮法、GPS水准法和重力测量法。短期验潮法是根据一定海域内陆海潮汐一致的特点，通过观测陆海各自距水尺零点的潮位高并求取高差，实现陆海高程的传递，其观测精度与时间成正相关。GPS水准法利用静态测量获得的高精度大地高差与似大地水准面差距之差来传递高程[1]。该方法相对实施周期短且方便实用，但前提是需要高精度的局部似大地水准面模型。李建成等已成功利用GPS观测所得的相对大地高差，联合精确的似大地水准面模型，将黄海高程传递到了距离上海30 km的洋山岛上，其精度与独立的潮位观测差值为厘米级，与三等水准测量相差为毫米级[1]。重力测量法应用重力位与高程的关系，计算陆地高程起算点的重力位值，根据跨海重力位差计算公式和海洋重力场资料计算出海域某点重力位值，确定该点相对陆地高程基准的高程值，实现跨海高程基准的精确传递。该方法可以快捷准确地将海域GPS大地高转化为1985国家高程系统的高程值，精度优于10 cm[2]。

三角高程测量是跨海高程传递中一种应用比较广泛的技术。其基本思想是根据由已知高程点向目标点观测所得的竖角和水平距离，计算两点间的高差，从而进行高程的传递[3]。欧阳桂崇等在一段10 km长的跨海段高程传递中，利用三角高程测量获得的结果与水准测量、重力测量、GPS水准及天文重力水准测量的符合精度均小于5 mm/km，达到二等水准要求。三角高程测量的精度主要受大气折光影响，在跨海高程传递中，《国家一、二等水准测量规范》(GB/T 12897—2006)规定采用大地四边形结构，利用同步对向观测方式来消除大气折光误差[3]。本文在此规范的基础上，提出一种线形结构的观测方式结合相对严格的同步对向观测，降低了原方式的复杂程度和观测量，取得了较好的效果。

二、精密三角高程测量原理

精密三角高程测量在三角高程测量基本原理的基础上，采用两台带有自动照准(ATR)功能的高精度全站仪，经改装后，照准棱镜固定在全站仪的把手上，同时进行对向观测，其高差计算公式如下[4]

hAB=0.5×[(SABtanαAB-SABtanαBA)-

(1)

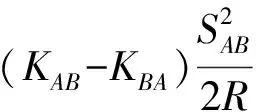
hAB=0.5×(SABtanαAB-SABtanαBA)

(2)

另外，在起始站和结束站上观测的高差计算公式为

hAB=SABtanαAB

(3)

三、测量方案

1. 点位布设

观测点位布设如图1所示。在测线S1—S2之间选择1、2、3三个临时点作为全站仪设站点。1点离S1点的距离及3点离S2点的距离限制为5～20 m，1、2点之间为跨海对向观测边，为了使对向观测边数是偶数，需设置2、3点之间为过渡对向观测边。另外，为了保证观测质量，要求1、2点之间通视良好，设置在较高处，使视线高出水面(一般在10 m以上)。

图1 观测点布设图

2. 仪器选用及改装

根据式(2)、式(3)可知，测量的精度取决于对向观测的平距值SAB及竖角观测值αAB、αBA的观测精度，由于跨海高程传递中竖角都非常小，SAB的测量精度很容易控制在1 cm以内，这样SAB的精度对最终高差的影响很小，可以不予考虑。因此，跨海高程传递测量的精度主要取决于测量仪器的竖角观测精度。本次选用的Leica TM30高精度智能全站仪测角精度为±0.5″，测距精度为±(1 mm+1×10-6D)，在ATR模式下测量范围为3000 m。精密三角高程测量需要对仪器进行必要的改装。改装后的仪器如图2所示，在TM30的把手位置安装圆棱镜，用于进行跨海段的对向观测。

3. 与传统方法比较

若按照传统的测距三角高程测量方式，根据规范要求需要布设成大地四边形，如图3(a)所示，两岸共需埋设4个固定点[4]，观测程序较为复杂。同时，跨海段观测视线为大地四边形的两条对边，各观测边将受到不同大气折光的影响，难以直接消除。

而采用改进后的线性结构布设方式(如图3(b)所示)，只需布设两个固定点，观测程序将在很大程度上得到简化，且观测视线可近似认为是对向观测，根据式(1)、式(2)相关理论，可以快速地消除大气折光的影响。

图2 改装后的TM30全站仪

图3 观测示意图

4. 观测方案

本次测量利用TM30的ATR功能，无人工照准测量。为保证观测质量，根据不同的气象条件，制订不同的对向观测方法，见表1。

表1 不同气象条件下的观测方案

续表1

此外，为减小测角中误差，一般采用多测回的方法。实际观测中每组观测4测回，保证每组的测角中误差都在0.5″之内。

(1) 起点观测

在1点架设全站仪，在S1点上架设棱镜杆，每个时段观测一组平距及竖角值。另外，测距前需观测温度与气压。

(2) 跨海段观测

跨海段对向观测采用距离观测与竖角观测分开进行的方式进行测量。在每个测量时段开始之前及结束之后进行距离观测，采用正倒镜测量的模式，取前后8次测量的平均值。

竖角的观测按照以下步骤进行：

1) 在1、2点上分别架设全站仪进行对向观测。按照表1所示的方案进行一个时段的观测。对向观测应按照严格的“同步”观测进行，即1、2点的观测间隔限制在5 min之内。

2) 若分上下午两时段观测，则在第二个时段开始前重新架设1点的全站仪(主要是仪器高的改变)，改变对向观测顺序，按方案1进行观测。

为保证时间上的一致性，最先观测的仪器多测一组，计算时，利用舒勒平均值原理，先将最先观测的5组两组之间取平均，然后对观测值取平均。

(3) 过渡边对向观测

将1点上的全站仪搬到3点架设，进行2、3点的对向观测，观测4个测回，对向观测共8个测回。变化仪器高，进行2、3点间的返测。

(4) 末点观测

将S1上的棱镜杆移动到S2上，保持棱镜的高度不变，在3点上对S2进行观测。在过渡边对向观测变化仪器高后，同样进行3、S2点间的返测。

四、数据处理及精度分析

1. 限差分析

根据《国家一、二等水准测量规范》(GB/T 12897—2006)的有关规定，二等水准测量每千米中误差Mw为2 mm，跨海段的总长为L，高差测量的中误差应不大于

该测量为8组，取其平均值，则每组测量的中误差应不大于

两组之间允许差值(中误差)为

2. 数据分析

项目共进行了两跨海段高程的传递，测段一、二的高差观测数据见表2。其中，测段一数据为一个时段观测模式所得；测段二数据分为上、下午两个时段观测模式所得。

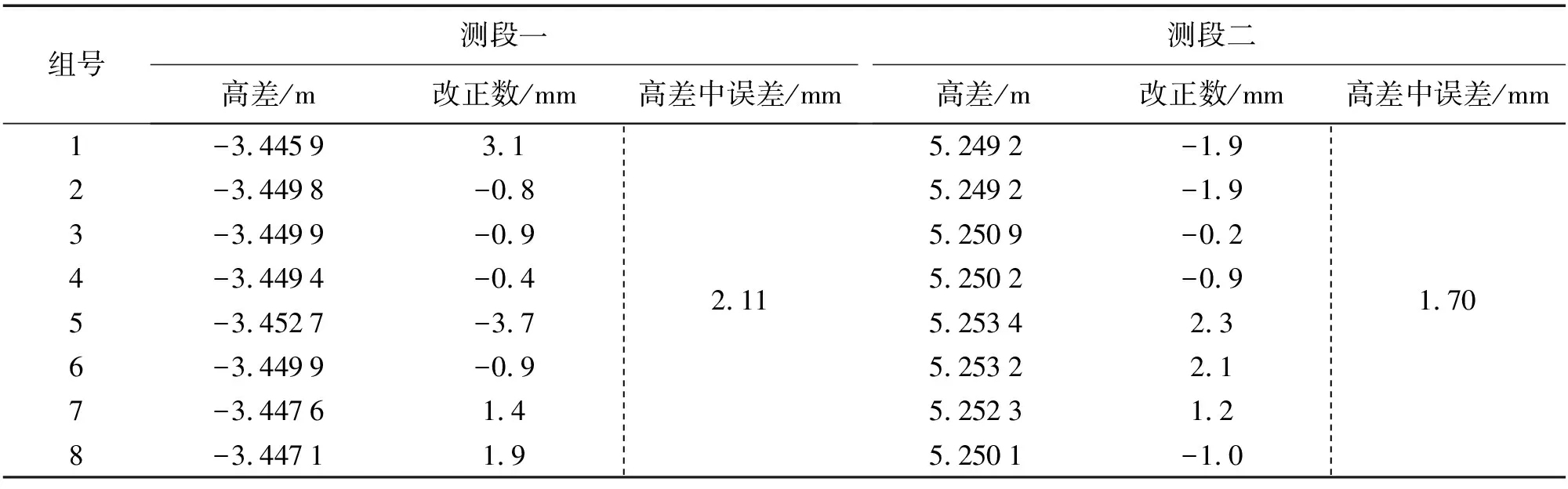
表2 高差观测数据

本次测量中测段一的长度为2.469 km，8组高差平均值为-3.449 0 m；测段二的长度为1.818 km，8组高差平均值为5.251 1 m。根据式(4)—式(6)计算各项限差与实际值相比较，结果见表3。

可以看出，测段一、二不论是高差中误差还是各组观测值间最大互差均小于限差规定的值，两个测段均达到二等水准的要求。

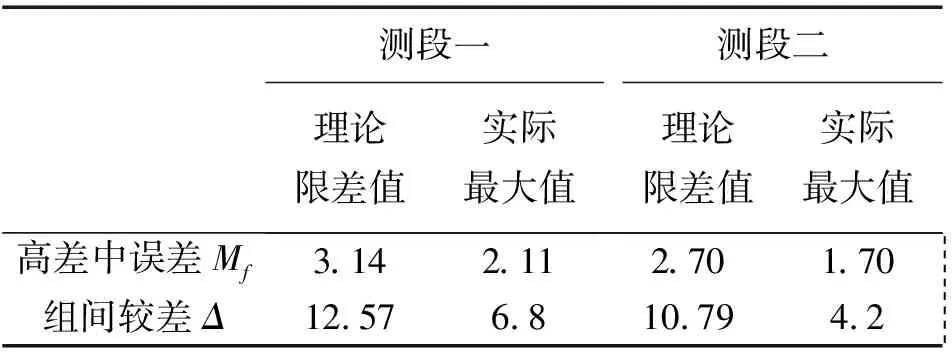
表3 限差与实际比较 mm

五、结束语

本文在国家规范的基础上，提出了一种线形观测结构，同时选用高精度的测量机器人进行相对严格的对向观测，削弱了大气折光的影响，采用偶数站的测量，避免了量取仪器高和觇标高的环节，简化了作业流程，提高了作业效率。最后对该方法在二等水准技术指标下进行了分析，证明精度达到二等水准的要求。

参考文献：

[1] 李建成，姜卫平.长距离跨海高程基准传递方法的研究[J]. 武汉大学学报：信息科学版，2001，26(6): 514-517.

[2] 鲍李峰,许厚泽,陆洋,等.利用重力位差实现跨海高程基准传递：中国，201110071065.1[P].2011-11-02.

[3] 国家测绘局.GB/T 12897—2006 国家一二等水准测量规范[S].北京:中国标准出版社,2006.

[4] 潘正风,杨正尧,程效军,等.数字测图原理与方法[M].武汉：武汉大学出版社,2004.

[5] 刘冠兰,李东宇，丁文宏.精密三角高程测量在宽水域跨河水准中的应用[J]. 工程勘察,2010，38(10)：71-74.

[6] 王知章,潘正风,刘冠兰. 三角高程测量在高铁特大桥无碴轨道施工测量中的应用[J].工程勘察,2009，37(6)：66-68.