基于新型趋近律的积分模糊滑模控制及其在PMSM控制中的应用*

刘红俐 张鹏 朱其新 胡寿松

1.苏州科技学院机械工程学院, 苏州 215009 2.华东交通大学电气与电子工程学院,南昌 330013 3.南京航空航天大学自动化学院, 南京 210016



基于新型趋近律的积分模糊滑模控制及其在PMSM控制中的应用*

刘红俐1张鹏2朱其新1胡寿松3

1.苏州科技学院机械工程学院, 苏州 215009 2.华东交通大学电气与电子工程学院,南昌 330013 3.南京航空航天大学自动化学院, 南京 210016

研究了基于新型趋近律的积分模糊滑模控制方法，并以永磁同步电机(PMSM)矢量控制系统为背景进行了应用研究。设计了基于新型趋近律的积分模糊滑模速度环控制器，有效地抑制了传统滑模变结构控制中的固有抖振问题。在滑模面的设计中引入误差信号的积分项，避免控制量中对加速度信号的要求，增强系统的抗干扰能力；引入了模糊控制，可以抑制滑模控制抖振。并提出一种新型趋近律，进一步对滑模抖振进行抑制，提高了滑模面的趋近速度。仿真表明，该方法能够实现精确的速度控制，与传统的滑模控制相比，该控制器具有更好的跟踪性能。

永磁同步电机；新型趋近律；积分模糊滑模控制；抖振

滑模控制(Sliding Mode Control，SMC)对参数变化及扰动具有强鲁棒性，同时滑模控制物理实现简单[1]。滑模控制的这些优点使得它很适合用于非线性系统的控制，但是控制系统的惯性、切换开关的时间滞后以及状态检测的误差等因素造成了滑模变结构控制的抖振问题。抖振的发生将影响系统的精确性，还可能激发系统未建模部分的强烈振动，对系统造成危害[2]。针对滑模控制中的抖振问题，国内外学者提出了众多的解决方案[3-8]。

永磁同步电机是一个多变量、强耦合、非线性、变参数的复杂对象，采用常规PID控制很难达到高性能控制的要求。本文根据PMSM调速系统的特点，设计了一种基于新型趋近律的积分模糊滑模变结构速度环控制器。在滑模面的设计中引入误差信号的积分项，避免控制量中对加速度信号的要求，增强了系统的抗干扰能力；同时引入了模糊控制，可以抑制滑模控制的抖振。在此基础上上，提出一种新型趋近律，进一步地对滑模抖振进行抑制，提高了滑模面的趋近速度。

1 永磁同步电机数学模型

永磁同步电机是一个非线性、高耦合系统。通常采用id=0的永磁同步电机转子磁场控制，转矩的大小只与定子电流幅值成正比，实现了永磁同步电机的解耦控制。在不影响控制性能的前提下，假设磁路不饱和，不计磁滞和涡流损耗的影响，空间磁场呈正弦分布，则永磁同步电机在d-q轴下数学模型如下[9]：

(1)

(2)

λq=Lqiq

(3)

λd=Ldid+LmdIdf

(4)

ωe=npωr

(5)

其中，id，iq分别为定子电流d，q轴分量；ud，uq分别为定子电压d，q轴分量；Rs为定子电阻；Ld，Lq分别为定子d，q轴电感；ωe为转子电角速度；ωr为转子机械角速度；λd，λq为d，q轴电子磁链；Lmd为d轴的互感；Idf为d轴等效磁化电流；np为极对数。

永磁同步电机的电磁转矩和机械方程如下：

Te=3np⎣LmdIdfiq+(Ld-Lq)·idiq」/2

(6)

(7)

其中，Tl是负载转矩；Bm是摩擦系数；J是转动惯量。当采用id=0的矢量控制时，电磁转矩公式可以简化为

Te=3npLmdIdfiq/2

(8)

由式(8)可以看出电磁转矩Te正比于q轴电流，这样就实现了永磁同步电机的解耦控制，使得控制永磁同步电机转矩也像控制直流电动机一样简单方便。从式(1)～(8)可以推出当永磁同步电机在id=0矢量控制下的d-q轴下状态方程为：

(9)

(10)

(11)

(12)

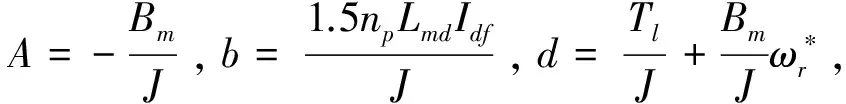
(13)

考虑系数的不确定性，有

(14)

2 积分模糊滑模控制器设计

2.1 积分滑模控制器设计

设计滑模变结构控制器的基本步骤包括2个相对独立的部分[10]：

1)设计切换函数S(x)，使它所确定的滑动模态渐进稳定且具有良好的动态品质；

2)设计滑动模态控制律u±(x)，使到达条件得到满足，从而在切换面上形成滑动模态区。一旦切换函数S(x)和滑动模态控制律u±(x)都达到，滑动模态控制系统就能完全建立起来。

确定切换函数S(x)：为了使系统滑动模态渐进稳定且具有良好的动态品质，本文引入积分滑模，积分滑模可以平滑转矩、减小系统稳态误差、削弱抖振、增强控制器的稳定性。引入积分项的切换函数S的基本形式如下：

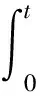
(15)

其中，c为正常数，c值大小影响系统速度响应趋于稳定的快慢。c值越大，趋于稳定的时间越短，反之则越长。但若c值取值过大，会加大滑模的抖振。c值具体设置还需根据具体情况来均衡。

确定滑模控制律u±(x)：为了使系统在有限的时间内到达并保持在滑动模态切换面上，本文选择基于新型趋近律的函数切换控制的变结构控制方案，函数切换控制表达式为u=ueq+ud。其中ueq为滑模等效控制部分，等效控制使系统状态保持在滑模面上，ud为滑模切换控制部分，切换控制使系统状态走向滑模线并稳定下来。

2.1.1 滑模控制律等效控制部分的确定

等效控制往往是针对确定性系统在无外加干扰情况下进行设计的。当忽略外加干扰d和系统的不确定项ΔD，系统的状态方程(14)变为

(16)

当系统在滑模面上滑动时有

(17)

将式(16)代入式(17)，可得

(18)

2.1.2 滑模控制律切换控制部分的确定

外加干扰d和系统的不确定项ΔD的存在会使系统状态偏离滑动模态，对此加入切换控制ud来实现对不确定性和外加干扰的鲁棒控制。切换控制的过程实质上就是趋近运动的过程。采用趋近律的方法可以改善趋近运动的动态品质。

常见的趋近律有等速趋近律、指数趋近律和变速趋近律。其中等速趋近律较为常用。等速趋近律的数学表达式如下：

(19)

其中，常数ε表示系统的运动点趋近切换面S=0的速率。等速趋近律的优点是结构简单，参数少，易于调试；缺点是趋近速度大的时候，引起的抖振也较大。针对等速趋近律的不足，高为炳院士于上世纪提出了指数趋近律的概念[11]，并设计了指数趋近律如下：

(20)

其中，S为滑模面,-kS为指数趋近项，在指数趋近中，趋近速度从一个较大值逐步减小到0。对于单纯的指数趋近，运动点逼近切换面是一个渐进的过程，不能保证在有限时间内到达，切换面上也就不存在滑动模态，所以增加一个等速趋近项-εsgn(S)，使得当S接近于0时，趋近速度是ε而不是0，可以保证有限时间到达。但是指数趋近律有自身的缺点，它的切换带为带状，系统在切换带中向原点运动时，最后不能趋近于原点，而是趋近于原点附近的一个抖振，此高频抖振可激发系统建模未考虑的高频成分，增加控制器的负担。

针对上述指数趋近律缺点，本文在常规指数趋近律的基础上，提出了一种新型指数趋近律：

(21)

ud=-ε·sgn(S)|S|α-ηS,ε>0,η>0

(22)

2.1.3 滑模控制律数学表达式

由上文可知滑模控制律包含2个部分:1)滑模控制等效部分；2) 滑模切换部分。由式(18)和(22)可知，滑模控制律数学表达式如下：

(23)

2.2 模糊控制器设计

根据滑模控制的原理，如果滑模控制器由等效滑模控制和切换控制两部分组成，则利用模糊规则，可建立基于等效控制和切换控制的模糊系统，从而消除抖振[12]。模糊控制规则如下：

1)IfS(x)is ZO then u isueq；

2)IfS(x)is NZ then u isueq+ud。

其中,模糊集ZO和NZ分别表示“0”和“非0”。

采用反模糊化方法，模糊控制器设计为

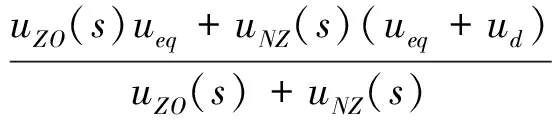
(24)

uZO(s)+uNZ(s)=1

(25)

当uNZ(s)=1时，u=ueq+ud，此时控制律为等效滑模控制。当uNZ(s)≠1时，通过隶属函数uNZ(s)的变化实现抖振的消除。采用一维模糊控制器，通过模糊控制律设计uNZ(s)。

模糊控制器的输入为S(x)，简记为S，模糊控制器输出为uNZ(S)。模糊控制器设计的具体步骤如下：

1)定义模糊集

S={NZP}，uNZ(s)={NZP}。

其中N为负，Z为0，P为正。

2)确定模糊规则

① If (Sis N) then (uNZ(s) is P)；

② If (Sis Z) then (uNZ(s) is Z)；

③ If (Sis P) then (uNZ(s) is N)。

模糊系统输入输出隶属度函数如图1所示。

图1 模糊系统输入输出隶属度函数

2.3 基于积分模糊滑模控制器的PMSM调速系统结构框图

图2为采用本文提出的基于新型趋近律积分滑模控制器，且id=0矢量控制方式的PMSM调速系统框图。采用转速、电流双闭环控制，其中转速环为外环，电流环为内环(包括d ，q 轴2个电流环)。

图2 系统结构框图

3 仿真分析

对PMSM调速系统进行仿真，建立了如图3所示的SIMULINK系统仿真模型图。

所采用的电机参数为：极对数pn=4，定子电阻Rs=2.875Ω，d轴电感Ld等于q轴电感Lq，即Ld=Lq=8.5mH，永磁体磁链LmdIdf=0.175Wb，转动惯量J=0.0008kg·m2，积分滑模参数c=2，摩擦系数Bm=0.0001N·m·s。

3.1 电机转速起动响应的仿真比较

首先，对基于等速趋近律的积分滑模控制进行了仿真。其中等速趋近律采用的参数如下：ε=0.35。在该控制策略下，给定转速ωr=30rad/s时系统的转速仿真波形如图4(a)所示。

图3 永磁同步电机滑模控制系统仿真模型图

然后，对基于等速趋近律的积分模糊滑模控制进行了仿真。其中等速趋近律采用的参数如下：ε=0.35。在该控制策略下，给定转速ωr=30rad/s时，系统的转速仿真波形如图4(b)所示。

最后，对基于新型趋近律的积分模糊滑模控制进行了仿真。其中新型趋近律采用的参数如下：ε=0.35，α=0.5，η=0.09。在该控制策略下，给定转速ωr=30rad/s时，系统的转速仿真图如图4(c)所示。

通过对图4(a)～(c)对比可知，采用等速趋近律积分滑模控制器的PMSM调速系统的转速在给定转速上下抖振很厉害。采用基于等速趋近律的积分模糊滑模控制器的PMSM调速系统的转速在给定转速上下抖振比基于等速趋近律的PMSM调速系统要小很多，但是起动响应的调节时间要长。而采用基于新型趋近律的积分模糊滑模控制器的PMSM调速系统在给定转速上下基本无抖振，而且起动响应的调节时间比基于前2种控制器的PMSM调速系统要短很多。由此可知，采用基于新型趋近律的积分模糊滑模控制器的PMSM调速系统在电机转速起动响应上性能更优。

3.2 电机转速跟踪响应的仿真比较

仍然采用上一小节的给定参数，PMSM调速系统的给定转速为ωr=30rad/s，在t=0.02时，给定转速变为ωr=50rad/s。分别对基于等速趋近律的积分滑模控制器，基于等速趋近律的积分模糊滑模控制器以及基于新型趋近律的积分模糊滑模控制器的PMSM调速系统进行转速跟踪响应仿真。仿真波形图如图5所示。

通过对比图5(a)～(c)可知，采用基于等速趋近律积分滑模控制器的PMSM调速系统在t=0.02s时转速发生变化，其跟踪时间为0.0068s，抖振很明显。采用基于等速趋近律的积分模糊滑模控制器的PMSM调速系统在给定转速发生变化时，其跟踪时间为0.0084s，抖振不明显。而采用基于新型趋近律的积分模糊滑模控制器的PMSM调速系统在给定转速发生变化时，其跟踪时间为0.0012s，抖振基本消失。由此可知，采用新型趋近律的积分模糊滑模控制器相对于前2种积分滑模控制器，在跟踪响应上性能更优。

图4 系统起动动态响应仿真结果

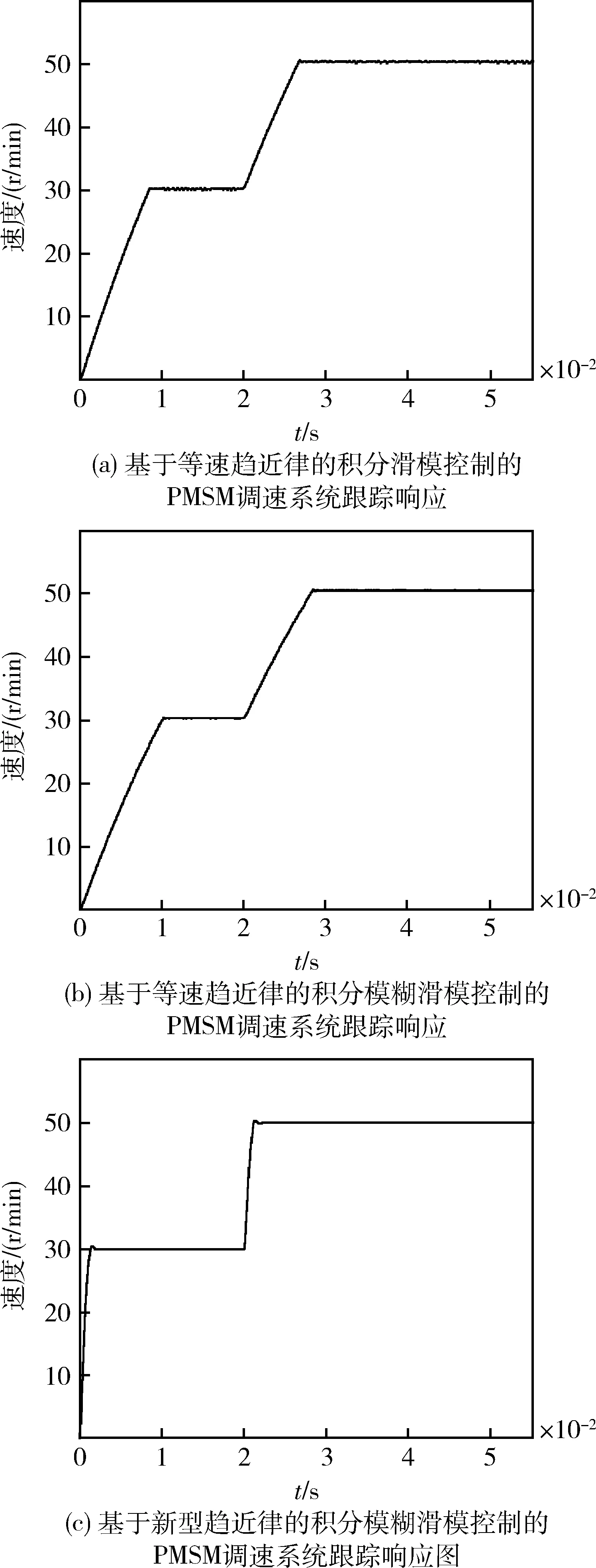
图5 系统跟踪动态响应仿真结果

4 结论

研究了基于新型趋近律的积分模糊滑模变结构控制方法，并以永磁同步电机矢量控制系统为背景进行了应用研究。设计了基于新型趋近律的积分模糊滑模速度环控制器，有效抑制了传统滑模变结构控制中的固有抖振问题。在滑模面的设计中引入误差信号的积分项，避免了控制量中对加速度信号的要求，增强了系统的抗干扰能力。同时，提出一种新型趋近律，进一步对滑模抖振动进行抑制，并提高了滑模面的趋近速度。

文中设计和实现了永磁同步电机转速控制系统。该系统运用矢量控制策略，采用转速电流双闭环控制结构，其中电流环采用PI 控制方法，转速环采用基于新型趋近律的积分模糊滑模控制策略。仿真结果表明该转速控制系统能够快速启动，并能快速精确地跟踪给定速度，较好地解决了永磁同步电机的高性能速度控制问题。如何实现新型趋近律下的PMSM的位置跟踪有待进一步研究。

[1] 刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007, 24(3):407- 418. (Liu Jinkun, Sun Fuchun. Research and Development on Theory and Algorithms of Sliding Mode Control[J]. Control Theory &Applications，2007, 24(3):407- 418.)

[2] 金鸿章,罗延明,肖真,张晓飞.抑制滑模抖振的新型饱和函数法研究[J].哈尔滨工程大学学报,2007, 28(3):288- 291.(Jin Hongzhang, Luo Yanming, Xiao Zhen, Zhang Xiaofei. Investigation of a Novel Method of Saturation Function for Chattering Reduction of Sliding Mode Control[J]. Journal of Harbin Engineering University, 2007, 28(3):288- 291.)

[3] Ryu S H , Park J H.Auto-tuning of Sliding Mode Control Parameters Using Fuzzy Logic[C]. Proc. of American Control Conf. 2001, 618- 623.

[4] 张天平,冯纯伯.基于模糊逻辑的连续滑模控制[J].控制与决策,1995,10(6)：503- 507.(Zhang Tianping, Feng Chunbo. Fuzzy Logic Based Continuous Sliding Mode Control[J]. Control and Dcision, 1995, 10(6): 503- 507.)

[5] Zhuang K Y , Su H Y , Chu J , Zhuang K Q. Globally Stable Robust Tracking of Uncertain Systems via Fuzzy Integral Sliding Mode Control[C]. Proc. of WCICA, 2000, 1827- 1831.

[6] 沈艳霞,纪志成.基于无源性永磁同步电机模糊滑模控制系统研究[J].系统仿真学报,2007, 19(17):4012- 4016. (Shen Yanxia, Ji Zhicheng. Passivity- Based Fuzzy Sliding- Mode Control System and Experiment Research for Permanent Magnet Synchronous Motors[J]. Journal of System Simulation, 2007,19(17):4012- 4016.)

[7] 刘姗梅,马迁,等.自适应模糊滑模控制在PMSM中的应用[J].微电机,2009, 42(5):43- 46. (Liu Shanmei, Ma Qian, et al.Application of Adaptive Fuzzy Sliding Mode Controller in Permanent Magnet Synchronous Motor[J].Micromotors Servo Technique, 2009, 42(5): 43- 46.)

[8] 张碧陶,皮佑国.基于模糊分数阶滑模控制的永磁同步电机控制[J].华南理工大学学报(自然科学版),2012, 40(3):126- 130. (Zhang Bitao, Pi Youguo. Control of Permanent Magnet Synchronous Motor Based on Fuzzy Fractional- order Sliding Mode Control[J]. Journal of South China University of Technology (Natural Science Edition), 2012, 40(3):126- 130.)

[9] Faa- Jeng Lin, Po- Hung Shen. Robust Fuzzy Neural Network Sliding- mode Control for Two- axis Motion Control System[J]．IEEE Transactions on Industrial Electronics，2006，53(4):1209- 1225．

[10] 刘金琨．滑模变结构控制MATLAB仿真[M].北京:清华大学出版社，2005.( Liu Jinkun.Matlab Simulation for Sliding Mode Variable Structure Control[M]. Beijing: Tsinghua University Press,2005.)

[11] 高为炳．变结构控制理论基础[M].北京: 科学技术出版社，1990.(Gao Weibing, Theoretical Principle of Variable Structure Control[M].Beijing:China Science & Technology Press,1990.)

[12] Chen J Y． Expert SMC-based Fuzzy Control with Genetic Algorithms[J]. Journal of the Franklin Institute，1999，336(4):589- 610.

TheIntegralFuzzySlidingModeControlBasedonaNovelReachingLawandItsApplicationsontheControlofPMSM

LIU Hongli1ZHANG Peng2ZHU Qixin1HU Shousong3
1. School of Mechanical Engineering, Suzhou University of Science and Technology, Suzhou 215009, China 2. School of Electrical and Electronic Engineering, East China Jiaotong University, Nanchang 330013, China 3. College of Automatic Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016，China

Theintegralfuzzyslidingmodecontrolapproachbasedonanovelreachinglawisinvestigatedinthispaper.Andthiscontrolapproachisverifiedinpermanentmagnetsynchronousmotor(PMSM)vectorcontrolsystem.Thespeedloopcontrollercaneffectivelysuppresstheinherentchatteringproblemintraditionalslidingmodevariablestructurecontrol.Toavoidtherequirementforaccelerationsignalincontrolandenhancethesystemanti-interferenceability,theslidingmodesurfacewitherrorsignalintegralitemsisproposed.Aimingatsuppressingthechatteringofslidingmodecontrol,thefuzzycontrolisintroduced.Atthesametime,anovelreachinglawwhichcanfurthersuppressthechatteringandimprovethereachingspeedisproposed.Theresultsofsimulationsshowthattheproposedslidingmodecontrollercanachieveaccuratespeedcontrol.Comparedwiththetraditionalslidingmodecontroller,theproposedslidingmodecontrollerhasbettertrackingperformance.

Permanentmagnetsynchronousmotor(PMSM);Novelreachinglaw;Integralfuzzyslidingmodecontrol(IFSMC);Chattering

*国家自然科学基金资助项目(51375323；61164014)

2014- 03- 27

刘红俐(1972-)，女，陕西米脂人，硕士，讲师，主要研究方向为伺服控制等；张鹏(1988-)，男，福建福清人，硕士研究生，主要研究方向为伺服控制等；朱其新(1971-)，男，安徽定远人，博士后，教授，主要研究方向为伺服控制和网络控制等；胡寿松(1937-)，男，南京人，教授，博士生导师，主要研究方向为故障诊断及复杂系统的自修复控制等。

TP273

： A

1006- 3242(2014)06- 0081- 07