BD2系统广域差分格网电离层模型研究与应用
2014-08-11崔莹莹贾为民
崔莹莹 孟 诏 贾为民 宋 帅
北京航天自动控制研究所,北京 100854
BD2系统广域差分格网电离层模型研究与应用
崔莹莹 孟 诏 贾为民 宋 帅
北京航天自动控制研究所,北京 100854

电离层延迟误差是影响BD2卫星导航系统定位测速精度的关键因素,如何减少电离层误差是当前卫星导航定位领域研究的热点问题。常见的电离层模型包括广域差分格网模型和Klobuchar模型,已有研究主要关注Klobuchar模型,对BD2广域差分格网模型的研究较少。本文分析比较了广域差分格网电离层模型和Klobuchar模型对电离层延迟误差的影响,并进行了真实环境下的评测。实验结果表明,使用广域差分格网电离层模型修正电离层延迟可以减小电离误差,从而提高单频接收机导航定位精度。
BD2系统;广域差分;格网电离层;电离层延迟误差
近年来,BD2卫星导航系统发展迅速,至2012年末,随着14颗北斗导航卫星进入预定轨道,导航系统已覆盖整个亚太地区,因此应用前景广阔,如何进一步提高定位测速精度是一个重要的研究方向。
对BD2卫星导航定位用户而言,电离层延迟误差是影响导航定位精度的主要误差源之一。电离层引起的误差一般为几米左右,但当太阳黑子活动增强时,电离层中的电子密度会升高,电离层延迟误差也随之增加,其值可达十几米甚至几十米。因此,电离层延迟误差是卫星导航定位中不可忽略的误差,在实际工程应用中必须加以修正。本文分别介绍了广域差分格网电离层模型和Klobuchar模型修正电离层误差的方法,通过接收机实际接收卫星信号分析了2种电离层模型对电离层延迟误差的影响。
1 电离层延时参数描述
电离层是一种散射介质,即其折射系数是电磁波频率的函数,其中电离层的群折射率计算方法为[1]:

(1)
电离层的相折射率为:

(2)
其中,f为载波频率,ne为电子密度,即单位面积上的电子数,它在不同的时间、不同的大气高度是不同的。
对于BD2卫星信号来说,载波以相速传播,而信号能量和伪码则以群速传播,则伪码在电离层中所受到的以m为单位的电离层延时Iρ为[1]:

(3)
载波相位测量值所受到的以m为单位的电离层延时Iφ为:

(4)
其中,Ne为在信号传播途径上的、横截面为1m2的通道空间里所包含的电子数总量。可见,弥散性的电离层降低了测距码的传播速度,造成伪距测量值变长;加快了载波相位的传播速度,造成载波相位测量值变短。
2 BD2系统电离层延迟格网模型
北斗二号卫星导航系统建设的广域增强系统(WAAS,Wide-Area Augmentation System)是由若干已知点位的参考站、中心站、地球同步卫星和具有差分处理功能的用户接收设备组成。北斗二号广域增强系统把复杂的电离层描述为距地面一定高度的薄层,并作为地面用户和站点的共同电离层参考面。在参考面上,北斗二号广域增强系统将特定区域按一定间隔分割成一定数量的网格,根据分布于WAAS系统区域内的一些监测站实时观察电离层延迟数据,对整个WAAS区域内的电离层状况进行估算,生成一定格式的电文,通过同步卫星传送给区域内广大用户,用户根据电文数据采用一定的算法获得其所观察到的卫星信号的电离层延迟值。
北斗二号广域差分系统将各格网点上的电离层延迟按WAAS格式实时播发给单频导航用户,接收机用户获得格网点上的电离层延迟改正量,还需要根据相应参数计算出观测时刻BD2信号从卫星到接收机的传播途径穿透电离层时的穿刺点位置及倾斜因子。图1为电离层穿刺点[2]的几何示意图。

图1 电离层穿刺点示意图
图1中,C为地心,O为用户机位置(φu,λu);A是穿刺点位置;O′是电离层下点;平均地球轨道半径Re=6378.137km;用户仰角E=∠BCO;穿刺点A的仰角E′=∠BCA;最大电子浓度距地面的高度hi=375km;地心角φpp=∠ACO。
对三角形ACO运用正弦定理,得:

(5)
可得地心角φpp的计算公式如下[3-4]:
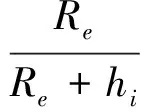
(6)
穿刺点的纬度:
φpp=arcsin(sinφucosφpp+cosφusinφppcosAz)
(7)
穿刺点的经度:
(8)
其中,Az为卫星方位角。
在计算出电离层穿刺点的经纬度后,可根据格网电离层修正算法计算穿刺点处的电离层延迟,具体算法如下。
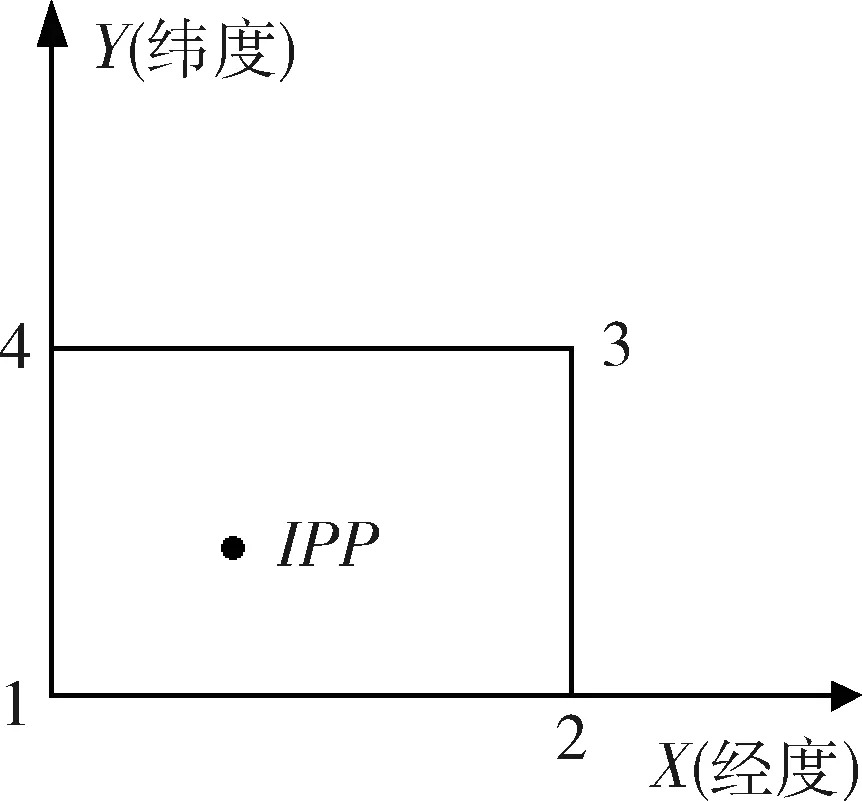
图2 用户穿刺点与格网点示意图
图2给出了用户穿刺点与所在格网点的示意图,其中IPP是用户接收机与某一颗卫星连线对应电离层穿刺点所在的地理位置,用地理经纬度(φpp,λpp)表示。周围4个格网点的位置分别用(φi,λi)(i=1,…,4)表示,格网点发播的天顶方向电离层延迟用VTECi(i=1,…,4)表示,穿刺点与4个格网点的距离权值分别用wi(i=1,…,4)表示。
当用户穿刺点所在周围4个格网点有效时,采用双线性内插法计算穿刺点处的电离层延迟,计算公式如下[5-6]:

(9)
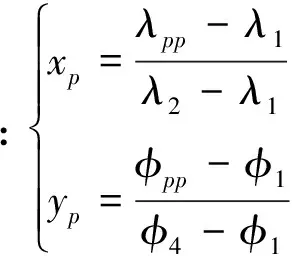
(10)
则权值分别为:
(11)
3 Klobuchar电离层延迟函数模型
Klobuchar模型是美国科学家Klobuchar于1987年提出的适用于单频接收机的电离层延时改正方法。Klobuchar模型是用半个余弦函数描述白天的电离层延迟变化情况,用一个常数描述午夜至凌晨之间的电离层延时,数学表达式为[6]:
I=
(12)
式中,A是余弦函数的振幅,T是值必定大于20h的余弦函数周期,两者分别用1个三阶多项式表示,数学表达式为:
(13)
(14)
上式中,系数α0,α1,α2,α3,β0,β1,β2和β3是地面控制系统根据日期及前5d太阳的平均辐射流量而选取的,并编入卫星的导航电文中发播给用户,φm为电离层穿刺点的地磁纬度。
Klobuchar模型代表了电离层时间延迟的周日平均特性,它取决于纬度和1d内的时刻。模型确定每天电离层的最大影响为当地时间的14点(即50400s),此时电离层中大气分子在阳光照射作用下分解最为旺盛,相应的电离层延时也达到最大值。由于Klobuchar模型是一种全球性统计经验型模型,而电离层在全球范围内变化十分复杂,因此,其修正精度不高,在高纬和赤道地区通常更差。经验表明,Klobuchar模型仅改正电离层影响的50%~60%,理想情况下可改正至75%[7]。
4 实验验证
为了分析广域差分电离层格网模型与电离层函数模型对电离层误差修正的差别,使用已在工程中应用的接收机,接收北斗B3频点信号,分别使用Klobuchar模型和电离层格网修正电离层延迟,并同时输出2种修正方法的定位结果。以1个已知点位作为定位结果参考点,对天进行连续拷机测试。数据采集时间从上午10点开始至下午16点,定位结果误差分析方法如下。
设卫星信号接收天线定位点坐标为P0(X0,Y0,Z0),接收机输出的定位结果为P(Xi,Yi,Zi)(i=1,…,N),则使用2种模型定位误差计算方法如下:

(15)
采用上述误差计算方法,分别计算2种电离层延迟修正算法的定位误差,误差分析如图3所示。
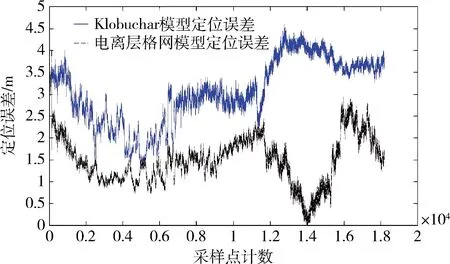
图3 Klobuchar模型与电离层格网模型定位误差图
从图3可以看到,经电离层格网模型修正后的定位结果误差明显优于Klobuchar模型修正的定位结果误差,其中在下午14时左右,格网电离层修正效果最好(对应图中第14000采样点左右),此时电离层延迟最大,对定位精度的影响也最大。将2种修正模型的定位误差相减,如图4所示。
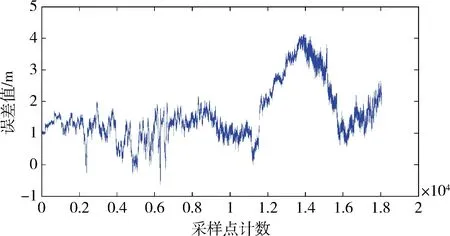
图4 Klobuchar模型与电离层格网模型定位误差的差值
图4显示了Klobuchar模型与电离层格网模型定位误差的差值大小关系,经计算,与采用Klobu- char模型修正的定位结果相比,经电离层格网模型修正后的定位结果精度提高可达4m。可见,采用北斗导航系统的广域差分电离层格网模型可以提高电离层延迟修正精度,从而改善单频定位精度。
5 结论
介绍了电离层延时对BD2卫星导航定位测速精度的影响,阐述了BD2广域差分格网电离层模型和Klobuchar模型修正电离层延迟的方法。经试验验证,与采用Klobuchar模型修正的定位结果相比,经电离层格网模型修正后的定位结果精度提高可达4m,从而提高了单频接收机的定位精度。
[1] 谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009:81- 82.
[2] Misra P, Enge P.Global Positioning System- Signals, Measurements, and Performance[M]. Ganga-Jamuna Press,2001:161- 169.
[3] Wide Area Augmentation System(WAAS) Specification[S].Federal Aviation Administration(FAA), FAA- E- 2892, May 9,1994.
[4] M B El- Arini, J A Klobuchar. The FAA Wide Area Differential GPS(WADGPS) Static Ionospheric Experiment[J].Proceedings of the ION National Technical Meeting 1993:485- 496.
[5] 黄智,袁洪,万卫星.WAAS电离层格网改正算法在中国地区部分站点的试算精度[J].全球定位系统,2003,(6):5- 10.(HUANG Zhi,YUAN Hong,WAN Weixing. The Test of FAA WAAS Ionospheric Grid Corrections Algorithm[J]. Gnss World of China,2003,(6):5- 10.)
[6] 北斗卫星导航系统空间信号接口控制文件公开服务信号(2.0版)[S].中国卫星导航系统管理办公室,BDS- SIS- ICD- 2.0,2013年12月.
[7] Parkinson B , Spiker J, Axelrad P, Enge P.Global Positioning System: Theory and Application[M].American Institute of Aeronautics and Astronautics, 1996:485- 515.
[8] Man- Lian Zhang, Sandro lL Radicella. Comparison Among IRI, GPS—IGS and Ionogram-derived Total Electron Contents[J].Advances in Space Research,2006 ,(37):972- 977.
TheResearchandApplicationofWideAreaDifferentialGridIonosphericModelinBD2System
CUI Yingying MENG Zhao JIA Weimin SONG Shuai
Beijing Aerospace Automatic Control Institute, Beijing 100854, China
TheionosphericdelayerroristhekeyfactoraffectingtheprecisionofpositionandvelocityoftheBD2satellitenavigationsystem,therefore,howtoreducetheionosphericerrorisextensivelyconcernedinthefieldofsatellitenavigationandpositioning.RegardingthetwofamousionosphericmodelsknownaswideareadifferentialgridmodelandKlobucharmodel,therelatedresearchismainlyfocusedontheKlobucharmodel,whiletheresearchonBD2wideareadifferentialgridmodelisless.ThedifferenceofwideareadifferentialgridmodelandKlobucharmodelintheionosphericdelayerroriscomparedandanalyzedinthispaper,andthedifferenceintherealsatellitesignalenvironmentisevaluated.Theexperimentalresultsshowthattheuseofthewideareadifferentialgridmodeltocorrectionosphericdelaycanreducetheionosphericerror,whichiscomparedwiththeuseoftheKlobucharmodel.Thus,thenavigationprecisionofsingle-frequencyreceiverisimproved.
BD2system;Wideareadifferential;Gridionospheric;Ionosphericdelayerror
2014- 03- 11
崔莹莹(1985- ),女,安徽蚌埠人,硕士,工程师,主要研究方向为导航接收机软件研究与设计;孟诏(1981- ),男,山东泰安人,硕士,工程师,主要研究方向为导航接收机软件研究与设计;贾为民(1961-),男,北京人,学士,工程师,主要研究方向为卫星导航技术;宋帅(1986- ),男,保定人,硕士,助理工程师,主要研究方向为导航接收机软件研究与设计。
V249.3
: A
1006- 3242(2014)06- 0012- 04
