气动干扰对串列双幅类流线形断面颤振的影响

刘小兵， 杨 群， 刘志文

(1. 石家庄铁道大学 风工程研究中心， 石家庄 050043； 2. 石家庄铁道大学 土木工程学院， 石家庄 050043；3. 湖南大学 风工程试验研究中心， 长沙 410082)

气动干扰对串列双幅类流线形断面颤振的影响

刘小兵1,3， 杨 群2， 刘志文3

(1. 石家庄铁道大学 风工程研究中心， 石家庄 050043； 2. 石家庄铁道大学 土木工程学院， 石家庄 050043；3. 湖南大学 风工程试验研究中心， 长沙 410082)

针对串列双幅类流线形断面，在均匀流场中进行了一系列的颤振稳定性风洞试验，并将试验结果与单幅类流线形断面的试验结果进行了对比。研究结果显示：气动干扰降低了双幅类流线形断面的颤振临界风速，间距越小，降低幅度越大；气动干扰增大了双幅类流线形断面的颤振频率，间距越小，增大幅度越大；与单幅类流线形断面相比，气动干扰使双幅类流线形断面的软颤振特性更明显。

气动干扰；串列双幅类流线形断面；颤振；风洞试验

近年来，随着社会经济的蓬勃发展，交通量日益增长。为了提高桥梁通行能力，通常将主梁设计成彼此分离且相互平行的双幅桥面。工程实践中，双幅桥面桥梁通常有两种形式：(1)桥梁新建时将主梁设计成分离平行的双幅桥面，两桥面同时建造并同时投入使用，如美国德克萨斯州1995年建成的跨越休斯顿航道的Fred Hartman桥、我国2006年建成的佛山平胜桥以及在建的青岛海湾大桥红岛航道桥等等；(2)在已建桥梁一侧再修建一座与其平行的桥梁，如美国分别于1950年和2007年建成的塔科马桥、日本分别于1985年和1996年建成的名港西桥以及韩国分别于1984年和2005年建成的珍岛桥等等。这两类桥梁主梁间距都不大，上游桥面与下游桥面在来流风作用下相互干扰，双幅桥面的风荷载、涡振特性及颤振稳定性等与单幅桥面相比存在一定的差异[1-2]。系统研究气动干扰对双幅桥面静力系数、涡激振动及颤振的影响规律对于双幅桥面桥梁的抗风设计具有重要意义。由于过去双幅桥面桥梁建设不多，所以目前相关的气动干扰研究文献相对较少，且主要是针对特定的桥梁工程展开的[3-10]。

本文以大跨度桥梁中经常应用的类流线形断面为对象，通过风洞试验研究了气动干扰对串列双幅类流线形断面颤振临界风速和颤振频率的影响，并从颤振导数出发分析了气动干扰机理。

1 风洞试验简介

风洞试验在湖南大学HD-2风洞高速试验段进行。采用弹性悬挂二元刚体节段模型的方式进行风洞试验。类流线形断面的几何参数见图1，单幅断面宽B=40.392 cm(不含风嘴的断面宽度b=30 cm)，高H=6 cm，宽高比B/H=6.732(不包含风嘴的断面宽度与断面高度之比b/H=5)。两幅断面之间的净间距为D。

为了方便改变试验参数，设计了针对双幅断面颤振气动干扰的试验装置，如图2所示。单幅节段模型由8根弹簧悬挂。在试验段上顶板和下底板分别固定两片槽钢。节段模型上方的4根弹簧通过带钩的活动螺栓和上顶板槽钢内的可滑动钢块连接。节段模型下方的4根弹簧通过带钩的活动螺栓与力传感器连接，力传感器再与下底板槽钢内的可滑动钢块连接。通过滑动槽钢内的钢块可以整体平移节段模型，实现上下游模型间距的改变。通过力传感器测量上下游断面模型的振动位移时程。为了有效防止模型在高风速下发生顺风向侧移，在模型来流前方大约10 m的位置固定两根立柱，通过细钢丝把立柱与模型两边的铁轴相连。

试验在均匀流场中进行，空风洞顺风向紊流度约为1%。首先进行单幅模型试验，然后进行不同间距串列双幅模型试验。对于双幅模型，选择了D/B=0.3、0.6、1.0、2.0、4.0和5.0六个间距进行研究。表1列出了试验参数。上下游模型的频率保持一致，阻尼大体接近。

图1 双幅类流线形断面的尺寸(单位：cm)Fig.1 Dimension of twin streamline-liked sections (unit: cm)

图2 风洞试验照片Fig.2 Photo of wind tunnel test

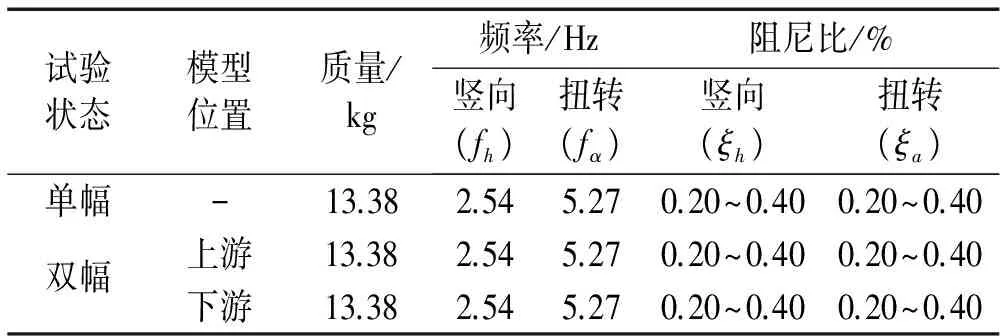
试验状态模型位置质量/kg频率/Hz阻尼比/%竖向(fh)扭转(fα)竖向(ξh)扭转(ξa)单幅-13．382．545．270．20～0．400．20～0．40双幅上游13．382．545．270．20～0．400．20～0．40下游13．382．545．270．20～0．400．20～0．40

2 气动干扰试验结果

图3为不同无量纲风速下单幅类流线形断面扭转角位移时程曲线及幅值谱。图4为D/B=0.6时不同无量纲风速下双幅类流线形断面扭转角位移时程曲线及幅值谱。图5为单幅类流线形断面与不同间距双幅类流线形断面扭转角位移根方差随无量纲风速变化曲线。图中无量纲风速Vr的定义如下：

(1)

其中，U为来流风速，ft为模型的扭转频率，B为模型宽度。

从图3～图5可以看到：(1)单幅断面接近无量纲颤振临界风速10.67时，扭转角位移急剧增大，表现出较明显的硬颤振形态。与单幅断面相比，双幅断面的软颤振表现得更明显。上下游两断面的扭转角位移根方差随无量纲风速的增大逐渐增大，变化曲线在颤振临界风速附近的斜率转折不如单幅断面明显。(2)同一无量纲风速，下游断面扭转角位移根方差大于上游断面扭转角位移根方差。这表明，与上游断面相比，下游断面的稳定性更差。(3)颤振过程中，上下游两断面振动并不同步，二者存在相位差。(4)上下游两断面的颤振频率保持一致，且介于固有竖向频率和固有扭转频率之间。

表2列出了按0.5°扭转角位移根方差标准得到的单、双幅类流线形断面的无量纲颤振临界风速及颤振频率。需要说明的是，表中双幅断面的颤振临界风速及颤振频率定义为干扰状态下稳定性相对较差的一幅断面对应的颤振临界风速及颤振频率。这一定义方式把两分离断面当作一个系统来考虑，而没有单独定义上、下游断面的颤振临界风速及颤振频率。笔者认为这符合双幅桥面桥梁颤振时的真实情况。

图3 单幅类流线形断面扭转角位移时程曲线及幅值谱Fig．3Curvesoftorsionalangulardisplacementversustimehistoryandamplitudespectrumofsinglestreamline⁃likedsection图4 双幅类流线形断面扭转角位移时程曲线及幅值谱(D/B=0．6)Fig．4Curvesoftorsionalangulardisplacementversustimehistoryandamplitudespectrumoftwinstreamline⁃likedsections(D/B=0．6)

图5 双幅类流线形断面扭转角位移根方差随无量纲风速变化曲线Fig.5 Curves of mean square root of torsional angular displacement versus dimensionless wind speed of twin streamline-liked sections

试验状态单幅类流线形断面双幅类流线形断面D/B=0．3D/B=0．6D/B=1D/B=2D/B=4D/B=5无量纲颤振临界风速10．674．876．267．469．5610．0010．20颤振频率3．995．054．864．634．244．174．11

图6和图7分别显示了不同间距双幅类流线形断面的无量纲颤振临界风速干扰因子IFv和颤振频率干扰因子IFf随D/B的变化曲线。本文定义颤振临界风速干扰因子和颤振频率干扰因子如下：

(2)

(3)

从图6可以看到：双幅断面的无量纲颤振临界风速在D/B=0.3时仅为单幅断面结果的45%；随着间距的增大，逐渐与单幅断面结果靠近；在D/B=5时约为单幅断面结果的95%。这表明：气动干扰降低了双幅类流线形断面整体的颤振临界风速，间距越小，降低幅度越大。

从图7中可以看到：双幅断面的颤振频率在D/B=0.3时为单幅断面结果的1.27倍；随着间距的增大，逐渐与单幅断面结果靠近；在D/B=5时约为单幅断面结果的1.03倍。这表明：气动干扰增大了双幅断面的颤振频率，间距越小，增大幅度越大，颤振频率越接近固有扭转频率。这也说明：双幅类流线形断面虽然仍发生弯扭耦合颤振，但随着间距的不断减小，弯扭耦合颤振形态逐渐向单自由度扭转颤振形态转移。

3 气动干扰机理分析

颤振导数是桥梁断面状态向量到自激力的传递函数。气动干扰对双幅桥面颤振的影响源于对上下游两桥面颤振导数的影响。鉴于此，本节基于颤振导数来分析串列双幅类流线形断面颤振的气动干扰机理。从前节试验结果可以看到，由于下游类流线形断面的颤振稳定性比上游类流线形断面差，双幅类流线形断面整体的颤振临界风速往往取决于下游类流线形断面的颤振临界风速，因此，本文着重通过对比单幅类流线形断面和双幅下游类流线形断面的颤振导数来分析气动干扰机理。

图6 双幅类流线形断面无量纲颤振临界风速干扰因子随D/B变化曲线Fig．6CurveofdimensionlessfluttercriticalwindspeedinterferencefactorversusD/Boftwinstreamline⁃likedsections图7 双幅类流线形断面颤振频率干扰因子随D/B变化曲线Fig．7CurveofflutterfrequencyandinterferencefactorversusD/Boftwinstreamline⁃likedsections图8 单幅类流线形断面与双幅下游类流线形断面的颤振导数(□单幅△D/B=1☆D/B=4)Fig．8Flutterderivativesofsingleandleewardstreamline⁃likedsection(□single△D/B=1☆D/B=4)

基于CFD软件Fluent计算了单幅类流线形断面和双幅下游类流线形断面的颤振导数。单幅断面颤振导数的获取过程如下：首先数值模拟断面分别做单自由度竖向强迫振动和单自由度扭转强迫振动，然后分别提取两种强迫振动下断面的升力和扭矩，最后基于升力和扭矩按最小二乘法确定颤振导数。识别双幅下游断面的颤振导数时，保持上游断面静止不动并强迫下游断面分别做竖向振动和扭转振动。通过提取下游断面的升力和扭矩来进行颤振导数识别。

4 结 论

本文通过风洞试验研究了气动干扰对均匀流场串列双幅类流线形断面颤振的影响，揭示了串列双幅类流线形断面的颤振气动干扰规律，分析了串列双幅类流线形断面的颤振气动干扰机理，得到了如下几点结论：

(1) 气动干扰降低了串列双幅类流线形断面的颤振临界风速，间距越小，降低幅度越大。

(2) 气动干扰增大了串列双幅类流线形断面的颤振频率，间距越小，增大幅度越大。

(3) 与单幅类流线形断面相比，串列双幅类流线形断面的软颤振特性更明显。

[ 1 ] Irwin P A, Stoyanoff S, Xie J M, et al. Tacoma Narrows 50 years later-wind engineering investigations for parallel bridges[J]. Bridge Structures: Assessment, Design and Construction, 2005, 1(1): 3-17.

[ 2 ] Larose G L, D’Auteuil A，Stoyanoff S. Aeroelastic model study for the twinning of the Tacoma Narrows Bridge[C]// The 4th International Conference on Advances in Wind and Structures. Jeju, Korea, 2008, 29-31.

[ 3 ] Kimura K, Shima K, Sano K, et al. Effects of seperation distance on wind-induced response of parallel box girders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6-7): 954-962.

[ 4 ] Sarkar P P, Jones N P, Scanlan R H. Identification of aeroelastic parameters of flexible bridges[J]. Journal of Engineering Mechanics, 1994, 120(8): 1718-1742.

[ 5 ] Sockel H, Watzinger J. Vibrations of two circular cylinders due to wind-excited interference effects[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74-76: 1029-1036.

[ 6 ] Honda A, Shiraishi N, Motoyama S. Aerodynamic stability of kansai international airport access bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1990, 33(1-2): 369-376.

[ 7 ] 陈政清, 刘小兵, 刘志文. 双幅桥面桥梁三分力系数的气动干扰效应研究[J]. 工程力学, 2008, 25(7): 87-93. CHEN Zheng-qing, LIU Xiao-bing, LIU Zhi-wen. Study of aerodynamic interference effects on aerodynamic coefficients of twin-deck bridges[J]. Engineering Mechanics, 2008, 25(7): 87-93.

[ 8 ] 朱乐东, 周奇, 郭震山，等. 箱形双幅桥气动干扰效应对颤振和涡振的影响[J]. 同济大学学报(自然科学版), 2010, 38(5): 632-638. ZHU Le-dong, ZHOU Qi, GUO Zhen-shan, et al. Aerodynamic interference effects on flutter and vortex-excited resonance of bridges with twin-separated parallel box decks[J]. Journal of Tongji University(Natural Science), 2010, 38(5): 632-638.

[ 9 ] 郭震山, 孟晓亮, 周奇,等. 既有桥梁对邻近新建桥梁三分力系数的气动干扰效应[J]. 工程力学, 2010, 27(9): 181-186,200. GUO Zhen-shan, MENG Xiao-liang ZHOU Qi,et al. Aerodynamic interferences of an existed bridge on aerodynamic coefficients of an adjacent new bridge[J]. Engineering Mechanics, 2010, 27(9): 181-186,200.

[10] 刘小兵, 陈政清, 刘志文, 等. 均匀风场中串列双矩形断面气动力干扰的数值研究[J]. 振动与冲击, 2008, 27(12): 83-87. LIU Xiao-bing, CHEN Zheng-qing, LIU Zhi-wen, et al. Numerical study on interference of aerodynamic force on two rectangular sections with tandem arrangement in uniform wind field[J].Journal of Vibration and Shock, 2008, 27(12): 83-87.

Effects of aerodynamic interference on flutter of twin streamline-liked sections in tandem

LIU Xiao-bing1,3，YANG Qun2，LIU Zhi-wen3

(1. Wind Engineering Research Center, Shijiazhuang Tiedao University, Shijiazhuang 050043, China；2. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;3. Wind Engineering Research Center，Hunan University, Changsha 410082, China)

A series of wind tunnel tests were performed to investigate flutter stability of twin streamline-liked sections in tandem. The test results were compared with those of a single streamline-liked section. The study results showed that the flutter critical wind speed of twin streamline-liked sections in tandem is decreased by aerodynamic interference, the smaller the distance between sections, the lower the flutter critical wind speed; the flutter frequency of two streamline-liked sections in tandem is increased by aerodynamic interference, the smaller the distance between sections, the higher the flutter frequency; the soft flutter characteristic of two streamline-liked sections in tandem is more obvious due to aerodynamic interference compared with that of a single streamline-liked section.

aerodynamic interference; twin streamline-liked sections in tandem; flutter stability; wind tunnel test

国家自然科学基金项目(50608030)

2013-02-19 修改稿收到日期：2013-05-30

刘小兵 男，博士，讲师，1982年3月生

TU311.3

A

10.13465/j.cnki.jvs.2014.08.028