桥梁防船撞钢套箱的碰撞力快速估算

潘 晋， 张 敏， 许明财

( 1. 武汉理工大学 交通学院，武汉 430063; 2. Centre for Marine Technology and Engineering (CENTEC), Instituto Superior Técnico, University of Lisbon, Lisbon, Portugal )

桥梁防船撞钢套箱的碰撞力快速估算

潘 晋1， 张 敏1， 许明财2

( 1. 武汉理工大学 交通学院，武汉 430063; 2. Centre for Marine Technology and Engineering (CENTEC), Instituto Superior Técnico, University of Lisbon, Lisbon, Portugal )

研究船舶与单墩桥梁防撞钢套箱艏尖舱的碰撞过程，探讨碰撞力快速估算及防撞装置模块化设计的可行性。首先采用非线性有限元方法模拟1 000吨级三峡标准散货船与钢套箱式桥梁防船撞装置的碰撞过程，分析了防撞钢套箱艏尖舱在不同的斜边角和船舶碰撞速度下的能量吸收特性以及传递至桥墩的碰撞力特性，得到的结果可为防撞钢套箱外形的选择提供参考。对所选择的防撞钢套箱形式，采用Boltzmann函数拟合了撞击船速与桥梁所受横桥向及顺桥向碰撞力之间的关系，该拟合公式可以用于此类防撞钢套箱方案设计阶段的撞击力快速估算。

船舶；桥梁；碰撞力；防撞钢套箱；有限元方法；

随着交通运输业的发展，通航船舶和桥梁的数目都大大增加，船舶撞击桥梁的概率呈逐年递增的趋势,因此研究船桥碰撞机理及桥梁防撞装置的设计很有必要。

在船桥碰撞机理方面，采用的分析方法主要有解析法和数值仿真法。解析法通常引用船舶碰撞领域中的一些成果，如Minorsky[1]根据船舶碰撞事故的统计结果,提出了结构变形能与参于变形的结构损伤体积之间呈线性关系。梁文娟等[2]给出了三维碰撞动力分析基本方程及其求解过程。Pedersen等[3]根据刚体碰撞力学理论分析了碰撞中的能量耗散问题等等。相比于解析法，数值仿真方法在船桥碰撞的研究领域应用更为广泛。刘建成等[4-5]采用数值方法分析了一艘4万吨载重量球鼻船艏与某长江大桥桥墩的碰撞，分析船桥碰撞力、能量转换以及桩基、承台和墩柱的冲击响应。李军等[6]对船桥碰撞数值模拟中涉及到的材料本构模型、流固耦合作用及其简化、桩土相互作用等问题进行总结归纳。潘晋等[7]通过数值方法计算了四艘不同吨位的三峡标准散货船在不同船速下的船桥碰撞力时程曲线，并将其计算结果与几种常用的船桥碰撞力估算公式进行了对比，得出了适合于散货船V型艏的船桥碰撞力计算公式。

对桥梁防船舶撞击的研究，不仅需要提高桥梁自身的强度，在有些情况下为了节约成本，可以采用各类的桥梁防撞装置来保护桥墩。潘晋等[8-9]采用有限元方法模拟了广州崖门大桥的桥墩钢套箱防撞装置与船舶之间碰撞，分析了防撞装置的影响因素，为桥墩防撞装置的设计提供参考。尹锡军[10]分析了国内外防撞装置，提出增加横向加筋肋和以圆管替换骨材能起到好的吸能效果。Wang等[11]提出在防撞装置中加一层钢丝绳圈能够起到缓冲作用，降低撞击力峰值，而且能够提供足够的时间对船舶起到导向作用。Peng等[12]对具有桩墩支撑的防撞钢套箱进行了数值仿真计算，提出增加橡胶层能明显降低碰撞力峰值。Pan等[13-14]采用数值方法模拟船舶撞击群桩式防撞装置过程，讨论了桩的水平大变形性能、桩与土之间相互作用的影响，对群桩式防撞装置进行了参数敏感度分析和优化。Lv等[15]基于ABAQUS对带有缓冲装置的简化模型进行仿真计算，得出带有缓冲设备的防撞装置对降低撞击峰值力和高能量的吸收起着显著的作用。Zhang等[16]基于LS-DYNA对桁架式防撞装置作了仿真计算，得出桁架式防撞装置利用杆件的弯曲能够吸收大量能量的结论。

由于船舶与桥墩防撞装置之间的碰撞是一个复杂的非线性动态响应过程，碰撞过程中的影响因素众多，很难建立一个精确的简化模型来表达两者之间的关系。同时，桥梁防撞装置作为一种较新的结构类别，至今尚无统一的设计标准可以遵循。因此，对于防撞装置的设计均需先进行方案设计，然后通过数值仿真方法来确定方案的可行性。这样的过程使得防撞装置的设计存在设计周期长、对设计人员要求高等特点，而在桥梁设计阶段需要能够快速设计防撞装置以及评估制造成本，因此有必要进行桥梁防船舶撞击装置的模块化设计方法研究，缩短桥梁及防撞装置的设计周期。

本文作为桥梁防船撞装置模块化设计研究一部分，在对已建和在建内河桥梁调研的基础上，选择单墩桥梁防1 000吨级船舶撞击的钢套箱式防撞装置作为研究对象。采用非线性有限元法模拟了1 000吨级三峡标准散货船与桥墩防护装置之间碰撞过程，分析了不同船舶撞击速度下单墩桥梁防撞装置艏尖舱角度对吸能效果和桥墩所受碰撞力的影响，选择出合适的防撞钢套箱外形。根据仿真结果，采用Boltzmann函数拟合了撞击船速与桥墩横桥向及顺桥向碰撞力之间的关系，该拟合公式可以用于此类防撞装置在方案设计阶段的撞击力快速估算。

1 船舶主尺度

目前长江三峡船舶要求按照标准船型进行设计，因此选择三峡库区标准船型中的1 000吨级散货船作为撞击船，其满载质量为1 419吨。图1为1 000吨级散货船船艏结构图，船体主尺度如下：船长Ls=65.5 m；垂线间长LB=63 m；船宽B=10.8 m；型深H=3.7 m；设计吃水Dd=2.6 m；结构吃水Ds=2.8 m。

图1 船艏结构图Fig.1 Geometry of ship bow

2 单墩钢套箱式防撞装置

钢套箱式防撞装置的俯视图和基本参数如图2所示，单位为m。防撞装置高2.5 m，板厚6 mm，肋骨尺寸为L70×50×6 mm，间距为500 mm，设置两道水平加强筋T10×100/8×200 mm。防撞装置斜边夹角θ如图2所示，在本文研究中θ的可取值范围为45°，50°，55°，60°，65°。

图2 防撞钢套箱Fig.2 Steel box of bridge protection

3 数值仿真

3.1 有限元模型

数值分析采用LS-DYNA模拟，有限元模型包括船体和防撞装置两部分，计算模型如图3所示。

本文目的是对艏尖舱外形选择进行研究，因此防撞钢套箱仅建立艏尖舱部分。船体模型是按照实际几何尺寸建立，采用梁单元、杆单元及壳单元进行模拟。由于船艏结构形式对撞击力影响很大，因此船艏结构采用精细网格，单元最大尺寸为0.25 m。船体中后部因远离撞击区，仅提供刚度和质量的影响，从平行中段到船尾最大单元尺寸为0.5 m。船体模型合理地分布集中质量进行配重，使整个模型的质量重心与实船重心位置一致。

3.2 材料

简化的解析方法通常采用刚塑性材料模型，其屈服应力为

(1)

式中初始屈服应力σ0为235 MPa；弹性模量E为2.06 ×1011N/m2；硬化模量Eh为1.18×109N/m2；密度ρ=7 850 kg/m3；泊松比μ=0.3。

碰撞是一个动态响应过程，材料的动力特性影响不能忽略。因此，在材料模型中引入应变率敏感性的影响，采用Cowper-Symonds本构方程

(2)

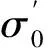
3.3 载荷和边界条件

本文的主要目的之一是探讨防撞钢套箱艏尖舱的斜边角度，仅考虑船舶正撞防撞装置斜边的工况, 即船舶航行方向与桥梁法向夹角为零的情况。防撞装置与桥墩连接部分约束所有自由度。内河船舶通过桥梁通航孔时不允许超速，速度应低于8节，本文在此范围内考虑三种撞击船速，分别为3.09 m/s、4.12 m/s和5.14 m/s。由于船舶碰撞运动主要是纵荡，采用附连水质量系数0.07来计入周围流体的作用[18]。不约束船体的转动与平动自由度，并施加初始速度。

4 单元尺寸的敏感度分析

在有限元分析中,合理的单元尺寸对于数值仿真计算的精度及运算效率影响很大。可以通过对比不同单元尺寸下的碰撞计算结果, 得出较适合的单元尺寸。

图4为撞击船速5.14 m/s时不同单元尺寸防撞装置模型的最大碰撞力和平均碰撞力随θ角的变化曲线，其中θ为防撞钢套箱的斜边角度；Es为单元尺寸；Ftm为桥墩所受的横桥向最大碰撞力；Fta为桥墩所受的横桥向平均碰撞力。由受力分析可知，θ角越大，桥墩所受的横桥向方向分力应该越小。而从图4中可以看到，当单元尺寸为1 m时，桥墩横桥向最大碰撞力出现异常现象，即θ=55°时的最大碰撞力大于θ=50°及θ=45°时的最大碰撞力；而单元尺寸为0.25 m时符合受力特点，未出现异常。分析其原因，是由于单元尺寸(Es=1 m)过大而造成的数值突变引起的。

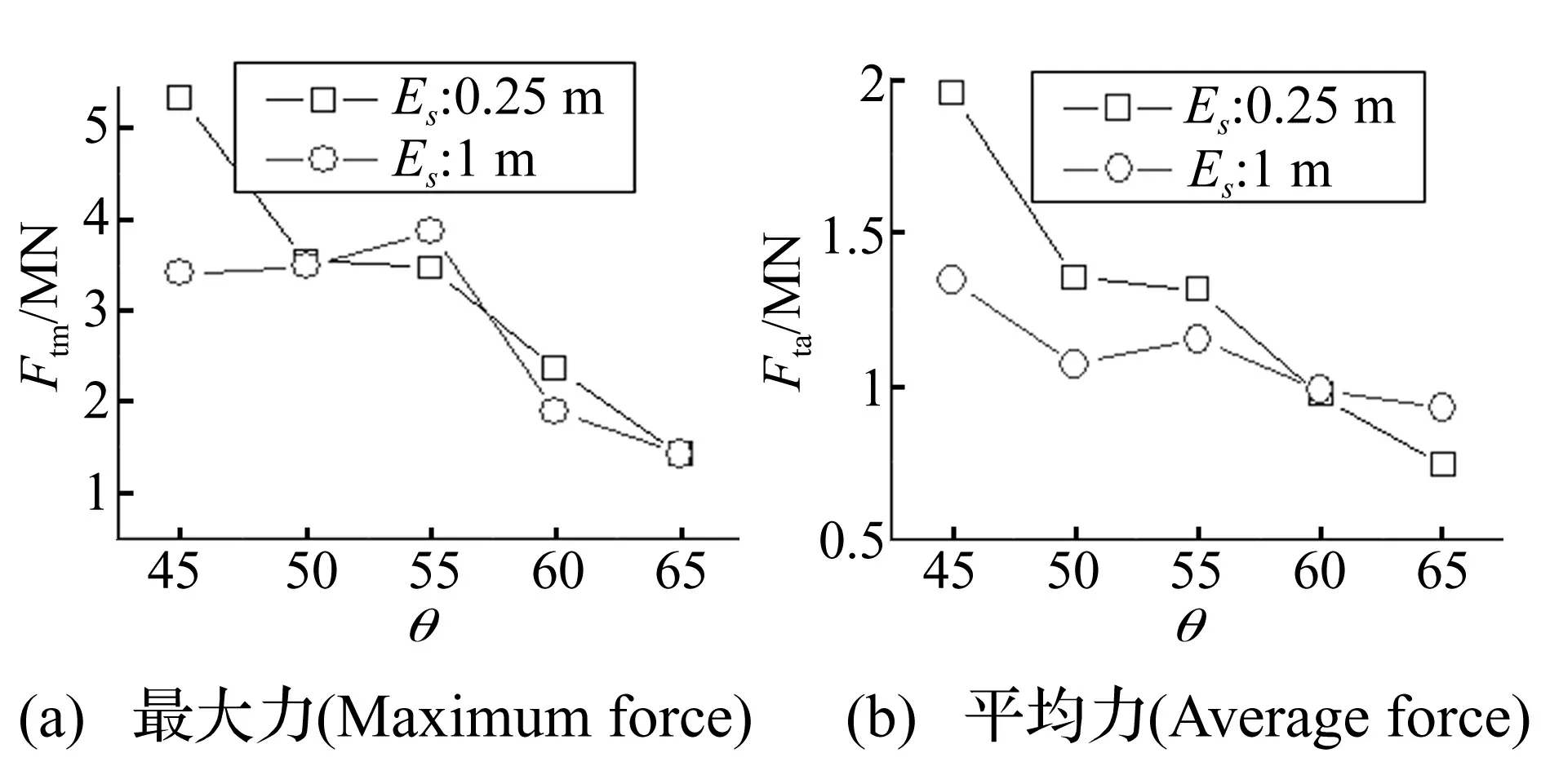
图4 不同单元尺寸下横桥向碰撞力Fig.4 Collision force with different element sizes

图5为撞击船速5.14 m/s时不同单元尺寸下的能量损耗随θ角的变化曲线，其中El表示碰撞能量的损耗。由图5可见，当防撞装置斜边为45°时，不同单元尺寸条件下能量损耗的计算值差别达到31%，而当碰撞角为65°时差别小于2%，这说明不同单元尺寸对碰撞仿真计算结果的影响很大，且对防撞装置而言，斜边角θ较大时数值计算结果对于单元尺寸的敏感度相对较低。

图5 能量损耗Fig．5Energyloss图6 应力分布图(θ=45°)Fig．6Stressdistributions

对比不同斜边角度的防撞装置数值仿真结果可知(限于篇幅仅给出撞击船速5.14 m/s、斜边角为45°时的应力分布示意图，如图6所示)，当防撞装置斜边角为45°、50°、55°时，防撞装置出现了单元失效情况，而当θ为60°和65°时船体和防撞钢套箱均没有出现单元失效。图7和图8分别表示Es=1 m及Es=0.25 m时桥墩横桥向碰撞力时程曲线。由图可知，当单元尺寸为1 m且斜边角为45°、50°、55°有单元失效情况时，出现了图7(a)圆圈内的数值突变；而当单元尺寸为0.25 m时(如图8(a)所示)，没有出现类似的现象。这是由于有限元数值仿真常以最大塑性失效应变来定义材料的失效，即当结构单元的等效塑性应变达到定义的单元最大塑性失效应变时单元失效，失效后的单元将不再参与后面的计算。因此当有单元失效时，如果单元尺寸过大就会造成数值跳跃，导致计算结果失真。在没有出现单元失效(即θ为60°和65°)时粗网格和细网格在最大碰撞力和碰撞力历程曲线都很接近，如图7 (b) 和图8 (b)所示，图中Ft为桥墩所受的横桥向碰撞力。

图7 碰撞力历程曲线 (Es=1 m, v=5.14 m/s)Fig.7 History curves of collision force

图8 碰撞力历程曲线 (Es=0.25 m, v=5.14 m/s)Fig.8 History curves of collision force

图9 内能随θ曲线Fig. 9 Internal energy- θ curves

上述分析结果表明，当数值仿真分析中有单元失效现象发生时，单元尺寸对最大碰撞力和能量损耗结果的影响较大，因此本文防撞钢套箱模型的最大单元尺寸取为0.25 m。

5 结果分析

图9和图10分别为不同船舶撞速下内能变化和桥墩所受碰撞力随θ值的变化曲线，其中Ei为内能变化；Flm为桥墩所受的顺桥向最大碰撞力；Fla为桥墩所受的顺桥向平均碰撞力；v为船舶撞击速度。由图可知，最大内能随θ的增加而减少，而同时碰撞力也减少。该现象说明防撞钢套箱主要是通过其斜边角度，使船舶运动方向发生偏转而沿防撞装置外侧滑走，碰撞结束时船舶仍保留较大动能，不完全是依靠防撞装置自身的破坏吸能来达到保护桥墩的目的。因此该防撞钢套箱在保护桥墩的同时，也具备良好的耐用性。

另外，最大内能的减小与θ角度存在非线性关系，θ角从55°增加到60°时，最大内能在不同船速下分别减少21% (v=3.09 m/s时)、34% (v=4.12 m/s时)和48% (v=5.14 m/s时)；而当θ角从60°增加到65°时最大内能变化均小于8%。因此，当θ大于60°后，再继续增大其斜边角度对提高防撞性能的效果已经不明显，θ为60°时能够获得较好的避碰效果，又能较好减少船体和防撞装置本身破坏程度。

对于桥梁防撞装置而言，一个重要指标是在安装防撞装置之后，船舶撞击下桥梁所受的横桥向和顺桥向力是否满足桥墩抗力要求。船体与防撞装置的碰撞角度变化会引起船体产生横向运动，从而改变碰撞持续时间及碰撞力。如图8所示，在θ为45°和50°时，其碰撞时间均约1.5 s，而当θ为55°、60°及65°时，其碰撞时间约为1 s。图10表示不同θ值的横桥向与顺桥向的最大碰撞力和平均碰撞力。由图可知，当θ在55°～65°之间时，其最大碰撞力和平均碰撞力呈减小趋势，减小的幅度随角度变化有所不同。当θ角从55°变为60°时，横桥向平均碰撞力在不同船速下分别减少31% (v=3.09 m/s时)、25% (v=4.12 m/s时)和26% (v=5.14 m/s时)，此时防撞装置总重增加13%；而当θ角从60°变为65°时，横桥向平均碰撞力仅分别减少7% (v=3.09 m/s时)、3% (v=4.12 m/s时)、24% (v=5.14 m/s时)，但防撞装置总重却增加了16%。同时，由图10(c)、(d)可知，虽然θ增加时横桥向碰撞力减小，但顺桥向碰撞力并不是随θ角度增加一直增加，当θ从55°增加到65°时，反而出现顺桥向碰撞力也同时减小的现象。因此，从桥墩所受的碰撞力以及经济性角度考虑，在目前的结构布置情况下θ为60°时可以获得比较好的防撞性能。

图10 碰撞力-θ曲线Fig.10 Collision force-θ curves

图11和图12分别是θ为60°时的船艏撞深-能量及撞深-碰撞力变化曲线，其中Ei、Ek和Et分别为内能、动能和总能量，Ft和Fl分别为横桥向和顺桥向碰撞力。在碰撞结束后内能只增加了1.13 MJ，而船体的速度为4.34 m/s，说明大部分的动能保留在船体内。θ为60o的防撞结构设计使船体在碰撞过程中从防撞装置边上滑走，故碰撞过程中防撞装置吸收的能量和撞深都很小。桥墩所受最大的横桥向和顺桥向碰撞力为1.5 MN和1.2 MN，且没有造成防撞装置的失效。这更进一步证明，该防撞装置的设计主要不是吸收船体的动能，而是通过改变船舶与防撞装置之间碰撞接触力的方向使船体偏离航向来降低船舶对桥墩的碰撞力。

图11 撞深-能量曲线(θ=60°，v=5．14m/s)Fig．11Curvesofcollisiondepth⁃force图12 撞深-碰撞力曲线Fig．12Curvesofcollisiondepth⁃energy

图13为桥墩碰撞力随船速变化曲线，从图中可以看出碰撞力随船速的增加而增大。最大碰撞力的非线

性特征比平均碰撞力明显，这是由于最大碰撞力受到瞬时单元失效及数值跳跃的影响较大，而平均碰撞力反应的是整个碰撞过程的平均受力，受单元失效的影响较小。

为快速评估斜边角θ为60°的防撞钢套箱碰撞力，采用Boltzmann函数对桥墩横桥向和顺桥向的最大碰撞力及平均碰撞力与撞击船舶速度之间的关系进行拟合，得出1 000吨级散货船撞击该防撞装置的碰撞力估算公式，方便该防撞装置的方案设计。为了增加拟合曲线的适用范围和减少计算误差，增加了三个撞击船速下的有限元计算结果用于拟合，分别为1.03 m/s、2.06 m/s和6.17 m/s。拟合的桥墩碰撞力方程如下(单位:MN)

(3)

式中:A1，A2，v0，dv为拟合的系数，F包括桥墩所受的横桥向、顺桥向的最大碰撞力及平均碰撞力，相应数值及含义见表1所示。

图13 碰撞力随船速变化曲线Fig.13 Collision force-velocity curves

图14 碰撞力拟合曲线有限元结果Fig.14 Fitting and FE results curves of collision force

Tab.1 Coefficient in the formulas of collision force

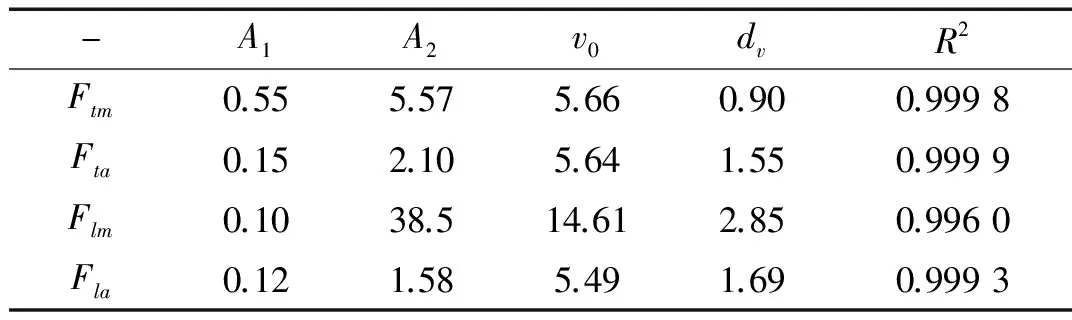
-A1A2v0dvR2Ftm0．555．575．660．900．9998Fta0．152．105．641．550．9999Flm0．1038．514．612．850．9960Fla0．121．585．491．690．9993

表1中的相关性R2可用于估计回归函数的精度，通过决定系数描述回归响应面模型与实际系统之间的相关性。图14为非线性有限元与拟合曲线计算结果的对比。对比结果表明R2均大于0.99，说明这四个公式可以很好地计算该防撞钢套箱在1 000吨级散货船碰撞下的碰撞力。由于拟合曲线的计算精度跟拟合时采用的数据范围有关，因此该公式仅适用于撞击船速范围为1～6 m/s时该类防撞钢套箱碰撞力的快速估算。

6 结 论

本文以三峡库区为研究背景，对单墩桥梁1 000吨级防船撞装置模块化设计中的相关内容进行了研究，主要结论如下：

(1) 当单元出现失效时，需要对数值仿真的单元尺寸灵敏度进行评估，单元尺寸太大会出现较大的数值跳跃，造成碰撞力结果的失真，影响计算结果。

(2) 桥墩所受的横桥向碰撞力与防撞装置斜边角度存在着一定的非线性关系。防撞装置斜边角度增加时横桥向碰撞力减小，而顺桥向的力并不是一直增加。从经济性及防撞装置适用性角度考虑，在目前的结构布置情况下，防撞装置采用60°斜边角度可以获得较好的防撞性能。

(3) 拟合的撞击力计算公式可用于1 000吨级散货船撞击该种防撞钢套箱时的碰撞力快速估算，但其适用的撞击船速范围在1 m/s至6 m/s之间。

虽然本文拟合的撞击力公式只适用于特定类型和布局的防撞装置，但如果能进行更加系统地分析，比如考虑桥墩的宽度、钢套箱的高度以及不同船舶类型、吨级等参数，就可以获得各种情况下的碰撞力快速估算公式，使防撞装置模块化设计成为可能，并可以此作为桥梁防撞装置方案设计阶段的依据。更系统的参数分析将作为下一步的研究内容。

[ 1 ] Minorsky V U．An analysis of ship collision with reference to protection of nuclear power ships[J]．Journal of Ship Research,1959,3(2)：1-4.

[ 2 ] 梁文娟,陈高增. 船舶碰撞力和能量吸收[J]. 交通部上海船舶运输科学研究所学报, 1992, 15(2):23-35. LIANG Wen-juan,CHEN Gao-zeng.Ship collision force and energy absorbability[J].Journal of Sssri,1992, 15(2): 23-35.

[ 3 ] Pedersen P T, Zhang S M. On impact mechanics in ship collisions[J]，Marine Structures, 1998,11(10):429-449.

[ 4 ] 刘建成，顾永宁，胡志强.桥墩在船桥碰撞中的响应及损伤分析[J].公路，2002(10)：33-41. LIU Jian-cheng,GU Yong-ning,HU zhi-qiang.Response and damage of bridge pier during ship-bridge collison[J]. Highway,2002(10):33-41.

[ 5 ] 刘建成，顾永宁. 基于整船整桥模型的船桥碰撞数值仿真[J]. 工程力学, 2003,20(5):155-162. LIU Jian-cheng,GU Yong-ning.Simulation of ship-bridge head-on collision based on finite element model of whole ship-bridge[J].Engineering Mechanice,2003,20(5):155-162.

[ 6 ] 李军，王君杰，欧碧峰.船桥碰撞数值模拟方法研究[J].公路,2010(10):14-19. LI Jun,WANG Jun-jie,OU Bi-feng.Research on numerical simulation of ship-bridge collision[J].Highway,2010(10):14-19.

[ 7 ] 潘晋，姜伟，许明财.散货船与桥墩碰撞力的经验公式与数值模拟对比研究[J].振动与冲击, 2012,31(19):123-127. PAN Jin，JIANG Wei，XU Ming-cai.Comparison of collision force between bridges and bulk carriers based on empirical formulas and numerical simulation[J].Jourmal of Vibration and Shock,2012,31(19):123-127.

[ 8 ] 潘晋， 吴卫国，王德禹,等.船-桥墩防护装置碰撞中的影响因素研究[J].武汉理工大学学报(交通科学与工程版)，2005, 29(4):538-541. PAN Jin,WU Wei-guo,WANG De-yu,et al. Uncertain factors research on collision between ship and anti-collision equipment [J].Journal of Wuhan University of Technology(Transportation Science & Engineering), 2005, 29(4):538-541.

[ 9 ] 潘晋, 吴卫国,王德禹,等.船-桥墩防护装置碰撞的有限元仿真[J].武汉理工大学学报(交通科学与工程版),2005, 29(2):178-181. PAN Jin,WU Wei-guo,WANG De-yu,et al. Finite element simulation to the collision between ship and anti-collision equipment [J]. Journal of Wuhan University of Technology(Transportation Science & Engineering),2005,29(2):178-181.

[10] 尹锡军.船桥碰撞及桥墩防撞设施研究[D].大连：大连海事大学，2006.

[11] Wang L L, Yang L M, Huang D J, et al. An impact dynamics analysis on a new crashworthy device against ship bridge collision[J]. International Journal of Impact Engineering, 2008, 35(8): 895-904.

[12] Peng S, Wu W G, Pan J, et al. Non-linear finite element drop collision simulation of the anti-collision device hitting a bridge pile cap[C]. Proceedings of the ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering,2010,OMAE2010-20351.

[13] Pan J, Wu W G, Xu M C.The design and analysis of pile protection devices for the Qiantang river bridge[C]. Proc29th Int. Conf. on Offshore Mechanics and Arctic Engineering; ASME paper, 2010a, OMAE2010-20346.

[14] Pan J, Wu W G, Xu M C. Optimization analysis of pile protection devices for Qiantang river bridge [C]. Proceedings of the Twentieth International Offshore and Polar Engineering Conference, 2010b, TPC-539.

[15] Lü W, Lu R L, Ning X L, et al. A mechanical calculation of the flexible & floating anti-ship collision device for bridge piers[J]. Advanced Materials Research, 2012, 479-481: 2540-2545.

[16] Zhang H, Fang S, Yin H T. Analysis of collision parameter about collision prevention device of bridge pier and optimum structural design[J]. Advanced Materials Research, 2012, 368-373: 1235-1240.

[17] Glykas A, Das P K, Barltrop N. Application of failure and fracture criteria during a tanker head-on collision[J]. Ocean Engineering, 2001, 28(4): 375-395.

[18] 王自力，蒋志勇，顾永宁.船舶碰撞数值仿真的附加质量模型[J].爆炸与冲击, 2002, 22(4): 321-326. WANG Zi-li, JIANG Zhi-yong, GU Yong-ning, An added water model for numerical simulation of ship collisions[J]. Explosion and Shock Waves, 2002, 22(4): 321-326.

Rapid estimation of collision force between a ship and a steel box for bridge protection

PAN Jin1, ZHANG Min1, XU Ming-cai2

(1. School of Transportation, Wuhan University of Technology, Wuhan 430063, China; 2. Centre for Marine Technology and Engineering (CENTEC), Instituto Superior T cnico, University of Lisbon, Lisbon, Portugal)

The design method of protection devices for single bridge pier in order to resist 1 000 DWT ship’s collision was studied. The nonlinear FE analysis was used to simulate a collision process between a Yangtze River standard bulk carrier and a steel box for bridge protection. The influences of the slope angle of the protection device bow and impact velocity of the ship on the energy absorption characteristics and the collision forces on the pier were investigated. The analysis results provided a reference for designing a steel box for bridge protection against ships collision. Boltzmann function was adopted to fit the relationship between velocities of the striking ship and collision forces of the bridge pier. The formula fitted could be used for rapid estimation collision forces in the primary design of this kind of protection device.

ship; bridge; collision force; steel box for bridge protection; finite element (FE) method

中央高校基本科研业务费专项资金资助(2013-VII-032 ； 2010-IV-084)

2013-10-21 修改稿收到日期：2013-12-04

潘晋 女，博士，副教授，1978年11月生

U663

A

10.13465/j.cnki.jvs.2014.08.012