地震模拟振动台三参量控制技术研究
2014-08-11栾强利陈章位徐进荣贺惠农
栾强利, 陈章位, 徐进荣, 贺惠农
(1.浙江大学 流体动力与机电系统国家重点实验室,杭州 310027;2.杭州亿恒科技有限公司,杭州 310015)
地震模拟振动台三参量控制技术研究
栾强利1, 陈章位1, 徐进荣1, 贺惠农2
(1.浙江大学 流体动力与机电系统国家重点实验室,杭州 310027;2.杭州亿恒科技有限公司,杭州 310015)
对地震模拟振动台三参量控制算法进行了深入的研究,详细研究了三参量反馈及前馈环节对振动台系统特性的校正作用,并通过仿真和试验的方法进一步验证三参量控制算法对地震模拟振动台系统频响特性的改善效果:通过引入三参量速度反馈可以有效扩展系统的频宽,引入三参量加速度反馈可以有效提高系统的阻尼,三参量前馈控制能够对消系统闭环传递函数中距离虚轴较近的极点,实现系统频宽的进一步扩展。最后,通过对三参量伺服控制的地震模拟振动台进行地震波形再现试验,证明三参量控制算法能够实现较高精度的地震波形再现试验。
地震模拟振动台;三参量控制;三参量伺服控制器;地震波再现
地震模拟振动台能够在实验室中真实再现地震时程曲线,是目前研究结构地震反应和破坏机理的最直接方法,广泛应用于土木工程、海洋结构工程、桥梁工程、水木工程等领域的抗震试验研究[1-4]。三参量控制算法70年代由日本学者提出,主要为了补偿单位移信号控制情况下地震模拟振动台频带不宽,不能实现加速度和速度控制的缺陷。目前,国内外大部分对频宽要求较高的电液伺服地震模拟振动台主要采用三参量控制方式,如哈尔滨工业大学的六自由度地震模拟振动台[5],浙江大学的双轴同向地震模拟振动台,日本的E-Defense[6]以及美国加州大学圣迭戈分校的足尺抗震振动台等[7]。
地震模拟振动台三参量控制的核心是三参量控制器,早期的三参量控制器主要通过模拟控制的方式实现,近年来,学者不断展开对三参量控制算法的应用研究,发表了一些具有创新性的研究成果[8-12],本文在上述研究成果的基础上,深入研究了三参量控制算法的原理,并通过仿真和试验方法,进一步研究了三参量控制算法对地震模拟振动台系统的校正作用,研究表明:加速度反馈增益能够有效提高系统的阻尼比,速度增益能够提高系统的带宽,位移反馈能够调节系统整体增益。三参量控制总体上改变了控制系统的极点配置,补偿了系统的共振频率,从而改善了频带特性[13-14]。
1 三参量控制原理
三参量控制器主要由三参量反馈控制和三参量前馈控制组成(图1)。三参量反馈控制通过引入位移反馈、速度反馈、加速度反馈,在保持系统稳定的前提下,提高了系统阻尼比和共振频率,从而扩宽了系统的频率使用范围;三参量前馈通过对伺服控制系统极点的配置,对消闭环传递函数中距离虚轴较近的极点,使系统工作频宽得到进一步扩展。
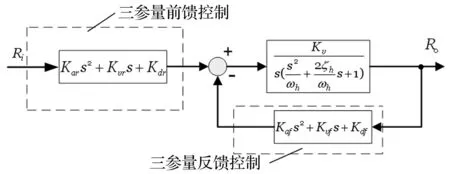
图1 三参量控制原理图Fig.1 Three-variable control (TVC) schematic diagram
1.1 三参量反馈控制
地震模拟振动台的开环系统传递函数可表示为
(1)
其中,ωh为液压系统固有频率,ζh为液压系统阻尼系数,kv为液压系统开环增益。
振动台系统中同时引入位移反馈、速度反馈、加速度反馈,形成三参量反馈控制系统。加入三参量反馈因子后的闭环系统如图2所示,其中,kdf为位移反馈增益,kvf为速度反馈增益,kaf为加速度反馈增益。
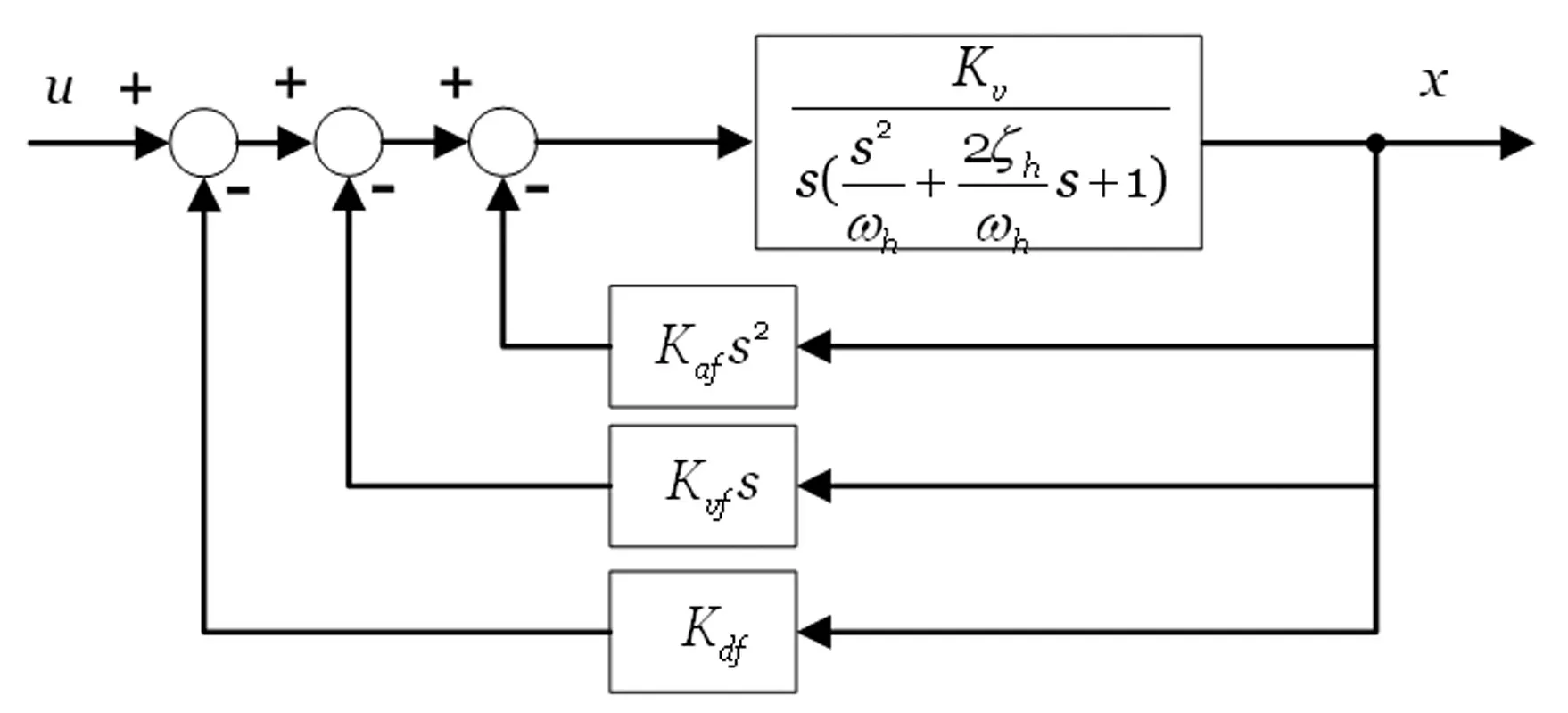
图2 三参量反馈控制Fig.2 Three-variable feedback control diagram
引入三参量反馈后的系统闭环传递函数:
(2)
上式等价于
(3)
其中,
(4)
从式(3)、(4)可见,增加kvf将使系统固有频率得到提高,增加kaf使系统阻尼比得到增加。
系统闭环传递函数(式3)分母为一个三阶函数,可分解为一个二阶函数和一个一阶函数两个环节相乘的形式,即
(5)
比较式(3)和式(5),得到
(6)
即
(7)
1.2 三参量前馈控制
上述地震模拟振动台系统是基于位移闭环控制系统设计的,而地震波一般是以加速度进行记录的,要进行地震模拟试验,就要求系统进行加速度控制。为进行加速度控制,三参量前馈输入装置要将加速度输入参考信号进行二次积分转换为位移信号;同时加入高通滤波器滤除低于振动台下限工作频率的低频信号。
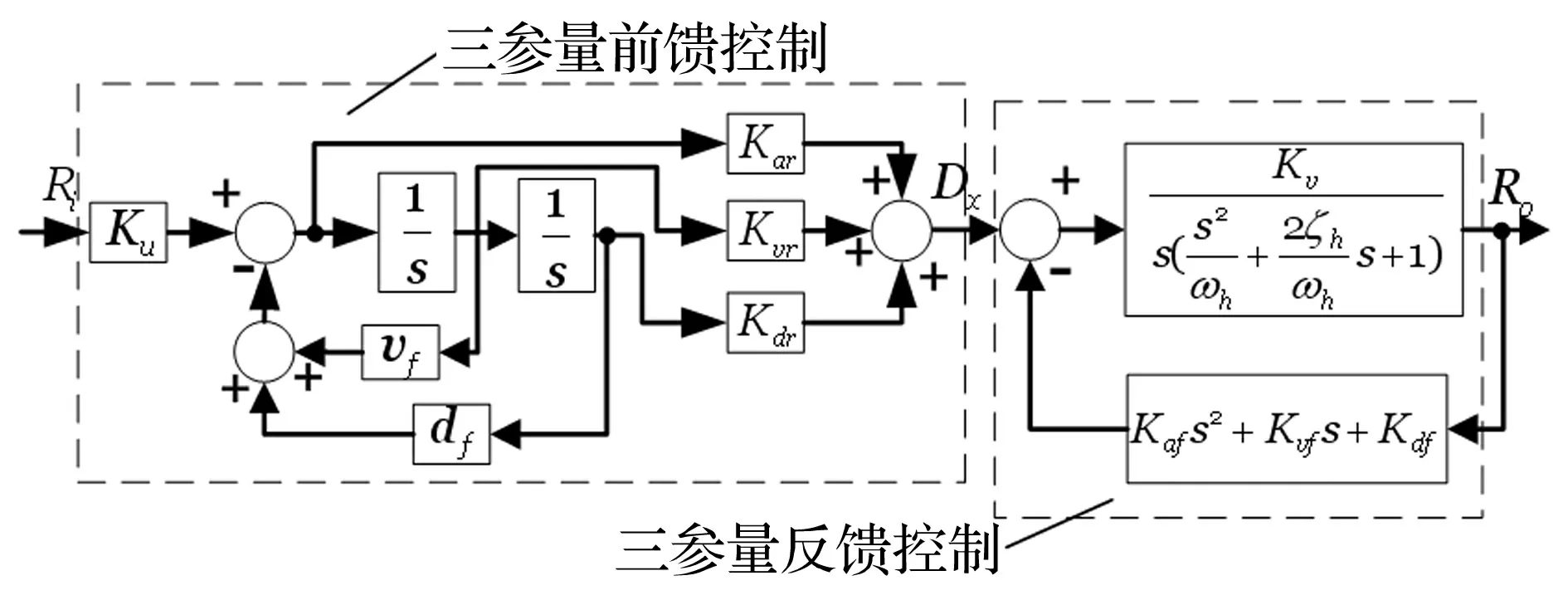
图3 三参量前馈控制Fig.3 Three-variable feedforward control diagram
加入三参量前馈控制后的系统框图如图3所示,其前馈传递函数
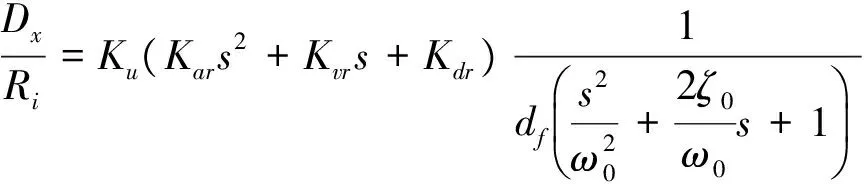
ω0和ζ0为高通滤波器的起点频率和阻尼比。通过选择合适的前馈因子Kars2+Kvrs+Kdr,可以将闭环传递函数W(s)中距离虚轴较近的极点进行对消,从而进一步扩展系统的工作频宽。
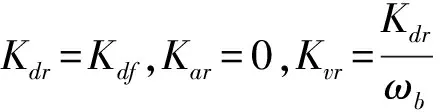
1.3 速度反馈的合成
地震模拟振动台系统一般没有配置速度传感器,但是三参量反馈需要有速度反馈信号。故需要由加速度信号经过积分、位移信号经过微分来合成速度信号,具体合成方法如下:
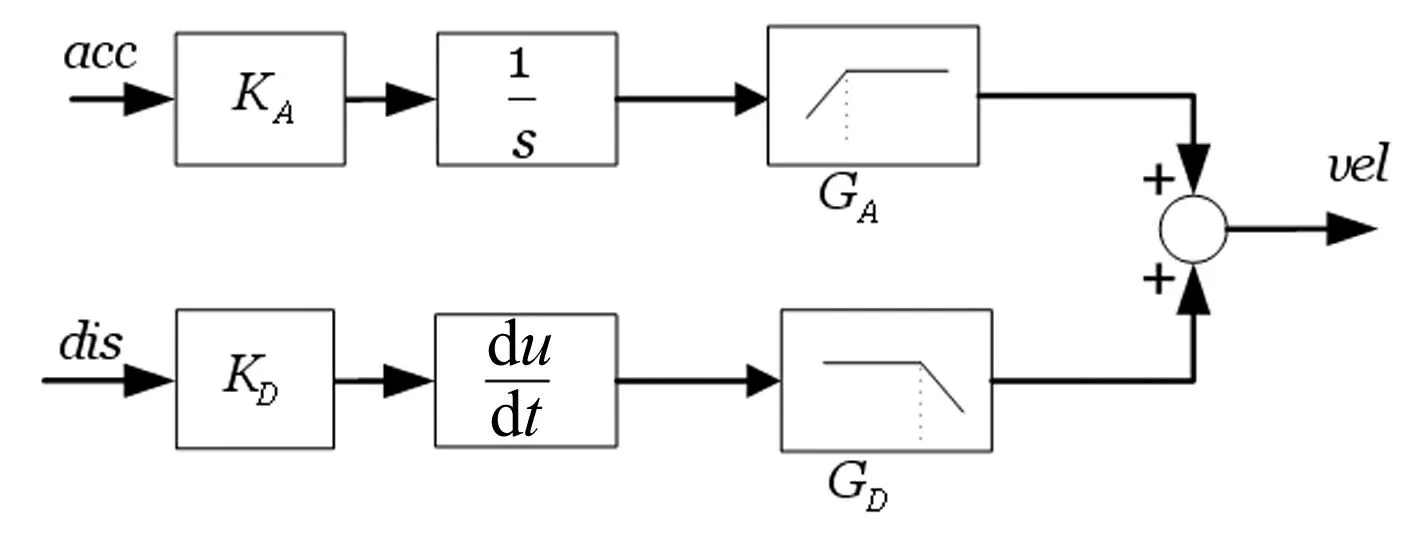
图4 三参量控制速度反馈合成Fig.4 Velocity feedback synthesis in three-variable control
图中GA为高通滤波环节,GD为低通滤波环节,KA和KD为对应加速度信号和位移信号的归一化参数。为了消除滤波环节引起的幅值和相位变化,GA和GD采用对称结构,
若GA选用二阶振荡高通滤波器,即
(9)
式中ωn为二阶系统固有频率,为待定系数,ζ为阻尼比,一般取ζ=0.7,则
(10)
为对应二阶的低通滤波环节,同样具有不改变信号的幅值和相位的特性。
2 三参量控制算法仿真
2.1 三参量控制算法仿真模型
为了进一步研究三参量控制算法对地震模拟振动台系统模型的控制效果,建立如图5所示的仿真模型,其中伺服阀看作比例环节,模拟振动台系统固有频率为40 Hz,阻尼比0.1,开环增益5,仿真模型考虑激振系统因伺服阀遮盖量、连接球铰间隙等引起的波形失真,引入了小量噪声信号。
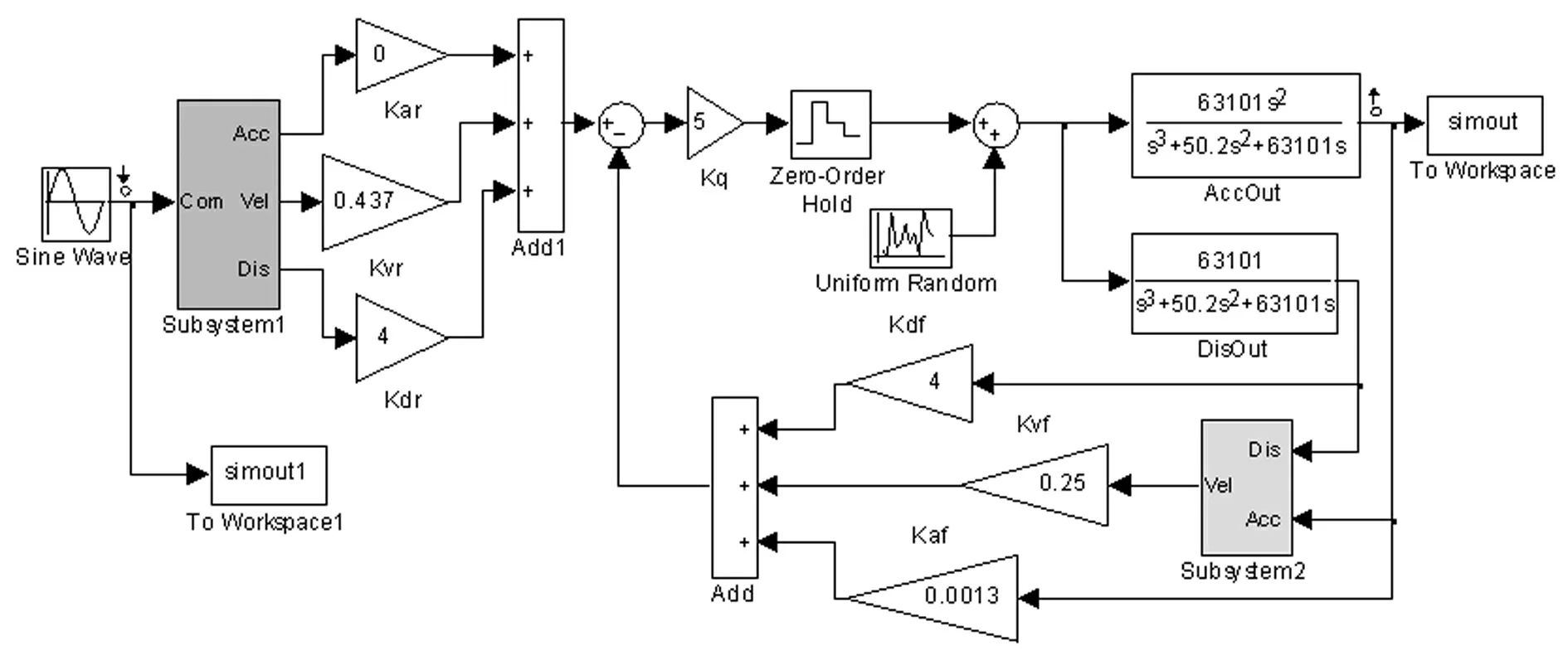
图5 三参量控制算法仿真模型Fig.5 Simulation model of TVC algorithm
仿真模型中,三参量前馈信号发生器模块如图6所示,输入为加速度控制指令信号,输出为加速度前馈、速度前馈、位移前馈信号;三参量反馈速度合成模块如图7所示,输入分别为位移、加速度反馈信号。

图6 三参量前馈信号发生器Fig.6 Signal generator in three-variable feedforward control

图7 三参量反馈速度合成Fig.7 Velocity synthesis in three-variable feedback control
2.2 三参量反馈控制算法仿真
对建立的三参量控制算法模型,首先考虑模型中只引入位移控制的情况,三参量控制参数如表1所示,图8为系统的Bode图。
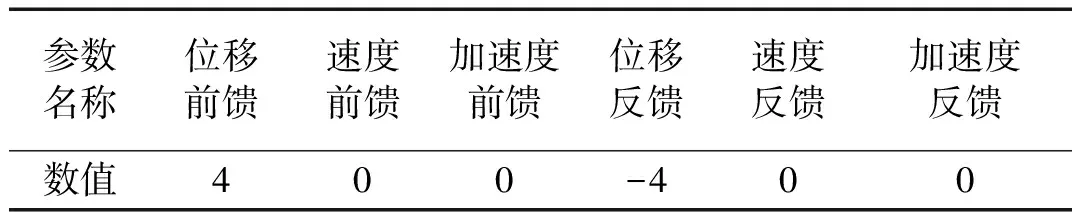
表1 三参量控制参数(一)

图8 三参量控制系统特性(一)Fig.8 System characteristics of TVC versus the parameters in Tab.1
由图8可知,系统响应幅值随着频率增加而衰减,3.25 Hz时幅值衰减3 dB,说明系统有效频宽为3.25 Hz。同时,系统40 Hz处存在共振峰,此即模拟振动台系统的油柱共振峰。
三参量控制系统中引入速度反馈信号,三参量控制参数如表2,图9为系统对应的Bode图。
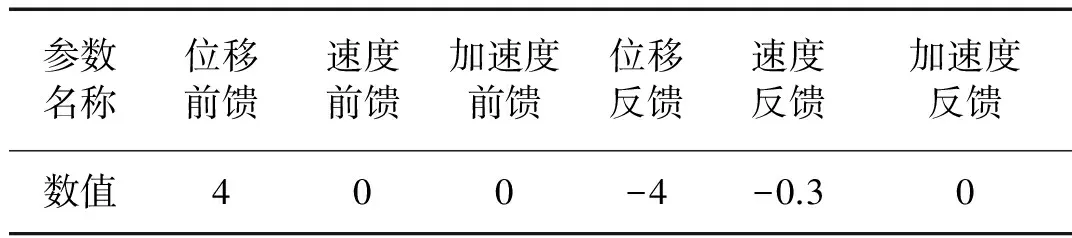
表2 三参量控制参数(二)

图9 三参量控制系统特性(二)Fig.9 System characteristics of TVC versus the parameters in Tab.2
由图9可知,系统共振峰移动至60 Hz,说明由于引入了速度负反馈控制,油柱共振频率提高了。同时,系统的共振峰值变大,说明速度负反馈导致系统的阻尼比降低。跟据公式(4),计算系统的共振频率63.2,阻尼比0.063。
进一步将加速度反馈信号引入三参量控制系统,三参量控制参数如表3,则系统对应的Bode图如图10所示。

表3 三参量控制参数(三)

图10 三参量控制系统特性(三)Fig.10 System characteristics of TVC versus the parameters in Tab.3
由图10可知,系统共振峰明显降低,说明由于引入了加速度反馈控制,系统的阻尼明显提高了,根据公式(4),系统的阻尼比为0.127。
以上三组仿真结果表明,通过引入速度反馈控制可以调整系统共振频率,通过引入加速度反馈控制可以调节系统阻尼系数,与理论分析一致。
2.3 三参量前馈控制仿真
在三参量反馈控制的基础上,进一步研究三参量前馈对系统的控制作用。引入速度前馈控制,三参量控制参数如表4所示,则系统Bode图如图11所示。

表4 三参量控制参数(四)
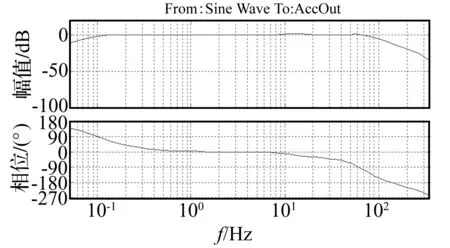
图11 三参量控制系统特性(四)Fig.11 System characteristics of TVC versus the parameters in Tab.4
由图11可见,系统Bode图幅值曲线的高频部分整体提升,曲线的平坦部分扩展到了60 Hz,说明通过引入三参量前馈控制,可以有效校正系统频响特性。
通过建立三参量控制系统的仿真模型,研究了三参量控制算法对系统传递特性的影响,仿真结果说明,三参量控制系统有效削低了油柱共振峰并扩展了系统工作频宽,能满足地震模拟试验的要求。
3 三参量控制系统试验分析
为进一步研究三参量控制算法对试验系统的作用,以浙江大学流体动力与机电系统国家重点实验室的地震模拟振动台为研究对象(图12),对三参量控制效果进行试验验证,振动台参数如表5所示,振动控制器选用杭州亿恒科技有限公司Premax振动控制器。

图12 地震模拟振动台Fig.12 Seismic simulating shaking table

名称技术参数台面质量/kg80台面尺寸/m1×1负载质量/kg100激振器工作面积Ap/m21.5×10-3油腔体积V/m31.67×10-4油液体积弹性模量β/(N·m-2)7×108伺服阀流量压力系数Kc/(m5·Ns-1)1.38×10-11激振器工作行程/m0.112管道系数η1.1
计算液压系统的固有频率和阻尼比:
3.1 正弦扫频试验
通过正弦扫频试验研究三参量控制对系统传递特性的影响,分别研究速度反馈控制、加速度反馈控制、三参量前馈控制对系统的实际控制效果。通过正弦扫频试验得到系统的传递函数,扫频频率范围为 5-100 Hz,加速度目标谱设置为0.5 g恒定值。
在不引入速度反馈及加速度反馈时,系统的传递函数如图13所示(为便于观察共振峰的变化,截取50-100 Hz图像),系统油柱共振峰约在75 Hz,与理论计算结果接近。通过引入速度反馈控制调节系统的共振频率,得到系统的传递函数如图14所示,系统油柱共振峰频率约在95 Hz,说明引入速度负反馈可以将系统的共振频率有效提高。
在速度反馈控制基础上,进一步引入三参量加速度反馈控制,系统的传递函数特性曲线如图15所示,通过引入加速度反馈,系统的油柱共振峰被明显削低了,说明有效增加了系统的阻尼。
三参量前馈控制的作用是对消闭环传递函数中距离虚轴较近的极点,达到扩展系统频宽的目的。试验中通过引入三参量前馈控制,系统的传递函数特性曲线如图16所示,曲线在5-90 Hz范围已经平坦,基本保持在±3 dB范围内(35-40 Hz处受地面连接共同作用的影响出现了结构共振),输出加速度信号能复现输入控制信号。试验表明,通过三参量控制,可以把系统传递函数特性曲线校正到理想的水平。

图13 系统传递函数(无速度、加速度反馈)Fig.13 System transfer function without velocity and acceleration feedback

图14 速度反馈时系统传递函数Fig.14 System transfer function with velocity feedback

图15 加速度反馈时系统传递函数Fig.15 System transfer function with acceleration feedback

图16 三参量控制系统传递函数Fig.16 System transfer function of TVC
3.2 地震模拟试验
地震波形再现试验一般以双闭环试验的形式进行,即在伺服控制器的基础上再加振动控制器进行闭环实时迭代控制。伺服控制器实现的内闭环是实现高精度波形再现的基础,内闭环控制性能较好,则进行实时迭代控制较为轻松,实现高精度波形再现也较为容易;反之则难以实现高精度的波形再现试验。
首先研究无外闭环迭代的情况下三参量伺服控制器的控制精度(开环试验),以典型的地震记录信号El-Centro地震波和Taft地震波通过三参量控制系统,观察输出波形的再现精度,输出波形如图17、18所示,其中虚线表示地震波目标波形,实线表示实验台面加速度波形。

图17 El-Centro地震模拟试验(一)Fig.17 EI-Centro earthquake simulating test (open-loop)

图18 Taft地震模拟试验(一)Fig.18 EI-Centro earthquake simulating test (open-loop)
系统开环试验中(传递函数不进行迭代修正),以El-Centro地震波的加速度信号为目标信号,得到振动台台面加速度波形如图17所示,该信号与输入目标信号(EI-Centro波)的时域相关系数为0.823;以Taft地震波作为目标信号得到振动台台面加速度波形如图18所示,该信号与输入目标信号(Taft波)的时域相关系数为0.830,可见,基于三参量控制的地震波再现试验具有较好的波形再现精度。
在三参量控制器的基础上结合外环振动控制器进行多次闭环迭代试验(传递函数不断修正),可以达到更高的地震波形再现精度。外环振动控制器做5次迭代之后的台面加速度波形如图19,图20所示,与地震波目标信号(EI-Centro波、Taft波)的相关系数分别达到了0.933、0.928。

图19 El-Centro地震模拟试验(二)Fig.19 EI-Centro earthquake simulating test (closed-loop)
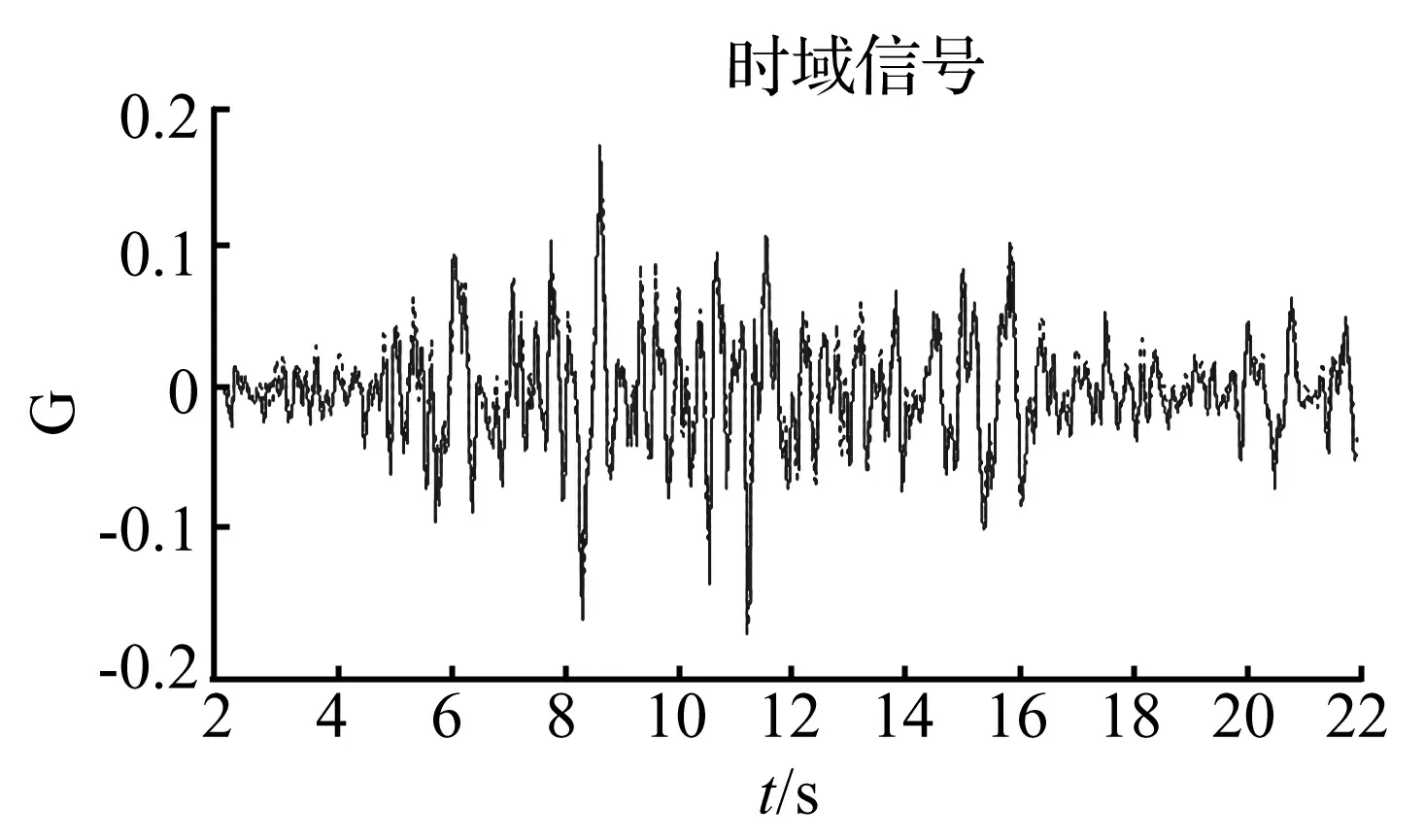
图20 Taft地震模拟试验(二)Fig.20 Taft earthquake simulating test (closed-loop)
地震模拟试验结果说明,三参量伺服控制器结合外部振动控制器能够快速实现高精度的地震波形再现。
4 结 论
地震模拟振动台将试件在地震作用下的反应从地震现场搬到实验室来进行,对于研究试件在地震过程中的破坏机理,缩短获取试验数据采集时间,提高结构抗震性能具有重要意义。地震模拟振动台往往系统固有频率较低、阻尼系数偏小,因此为了扩展系统的频宽,增加系统的阻尼比,可以通过伺服控制器对系统的传递特性进行校正。
三参量控制算法能够有效扩展系统频宽,增加系统阻尼比,本文在对三参量控制算法进行深入研究的基础上,详细探讨了三参量反馈环节和三参量前馈环节对系统传递特性的校正作用,并通过仿真和试验的方法,进一步验证了三参量控制对地震模拟振动台系统特性的改善作用,研究表明:
(1) 三参量反馈控制中通过速度反馈可以有效扩展系统的频宽;
(2) 三参量反馈控制中通过引入加速度反馈可以有效增加系统的阻尼比,降低系统在共振频率点的响应;
(3) 三参量前馈控制器通过对消闭环传递函数中距离虚轴较近的极点,达到进一步扩展系统频宽的目的;
(4) 地震模拟振动台三参量控制,提高了系统的频率响应特性,使地震模拟振动台在地震波形再现试验过程中,具有较高的波形再现精度。
[ 1 ] 黄浩华. 地震模拟振动台的设计与应用技术[M]. 北京:地震出版社, 2008.
[ 2 ] 邱法维,钱稼茹,陈志鹏. 结构抗震实验方法[M]. 北京:科学出版社,2000.
[ 3 ] 邱法维, 沙锋强, 王刚,等. 地震模拟振动台控制技术及软件研究[J]. 液压与气动, 2011(6): 98-101. QIU Fa-wei, SHA Feng-qiang, WANG Gang, et al. Shaking table control technology and software research [J]. Chinese Hydraulics and Pneumatics, 2011(6): 98-101.
[ 4 ] 唐贞云, 李振宝, 纪金豹,等. 地震模拟振动台控制系统的发展[J]. 地震工程与工程振动, 2009, 29(6): 162-169. TANG Zhen-yun, LI Zhen-bao, JI Jin-bao, et al. Development in shaking table control system [J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(6): 162-169.
[ 5 ] 韩俊伟, 李玉亭, 胡宝生. 大型三向六自由度地震模拟振动台[J]. 地震学报, 1998, 20(3): 327-331. HAN Jun-wei, LI Yu-ting, HU Bao-sheng. Large scale 3 dimension and 6 degree of freedom shaking table [J]. Earthquake Science, 1998, 20(3): 327-331.
[ 6 ] Tagawa Y, Kajiwara K. Controller development for the E-Defense shaking table [J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2007, 221(2): 171-181.
[ 7 ] Shortreed J S, Seible F, Benzoni G. Simulation issues with a real-time, full-scale seismic testing system [J]. Journal of Earthquake Engineering, 2002, 6(s1): 185-201.
[ 8 ] Stoten D P, Shimizu N. The feedforward minimal control synthesis algorithm and its application to the control of shaking-tables [J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2007, 221( 3 ): 423-444.
[ 9 ] Ammanagi S, Poornima V, Sera A, et al. Development of a digitally-controlled three-axis earthquake shake table [J]. Current Science, 2006, 91(2): 190-203.
[10] 王燕华, 程文瀼. 地震模拟振动台运动控制性能分析[J]. 振动与冲击, 2010, 29(2): 99-106. WANG Yan-hua, CHENG Wen-rang. Dynamic property of a shaking table simulating earthquake [J]. Journal of Vibration and Shock, 2010, 29(2): 99-106.
[11] 杨志东. 液压振动台振动环境模拟的控制技术研究[D]. 哈尔滨: 哈尔滨工业大学,2009.
[12] Xu Y, Hua H X, Han J W. Modeling and controller design of a shaking table in an active structural control system [J]. Mechanical Systems and Signal Processing, 2008, 22(8): 1917-1923.
[13] 韩俊伟,于丽明,赵慧,等.地震模拟振动台三状态控制的研究[J].哈尔滨工业大学学报, 1999, 31( 3): 21- 28. HAN Jun-wei, YU Li-ming, ZHAO Hui, et al. Study of three state controller of seismic simulating shaking table [J]. Journal of Harbin Institute of Technology, 1999, 31( 3): 21- 28.
[14] 李振宝, 唐贞云, 纪金豹. 地震模拟振动台三参量控制算法超调修正[J]. 振动与冲击, 2010, 29(10): 211-215. LI Zhen-bao, TANG Zhen-yun, JI Jin-bao. Overshoot modification of shaking table TVC algorithm [J]. Journal of Vibration and Shock, 2010, 29(10): 211-215.
Three-variable control technique for a seismic analog shaking table
LUAN Qiang-li1, CHEN Zhang-wei1, XU Jin-rong1, HE Hui-nong2
(1. The State Key Lab of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China;2. Hangzhou ECON Science and Technology Co., Ltd., Hangzhou 310015, China)
Three-variable control (TVC) algorithm for a seismic analog shaking table was studied deeply, and the correction action of the three-variable feedback and the three-variable feedforward step on the characteristics of the shaking table system was investigated in detail. Through simulation and field tests, the improvement effect of the three-variable control technique on the system frequency response characteristics of the seismic analog shaking table was verified. The system frequency bandwidth was expanded effectively by introducing the velocity feedback of TVC. The system damping was raised by introducing the acceleration feedback of TVC. The pole points of the system closed-loop transfer function close to the imaginary axis were eliminated and the system bandwidth was further extended by introducing the three-variable feedforward control. Finally, by conducting the seismic wave reproduction test on a three-variable controlled shaking table, it was shown that the TVC algorithm can realize a higher-precision seismic wave reproduction test.
seismic analog shaking table; three-variable control (TVC); TVC servo controller; seismic wave reproduction
2013-04-09 修改稿收到日期:2013-05-22
栾强利 男,博士生,1984年生
陈章位 男,教授,博士生导师,1965年生
TB534; TH137
A
10.13465/j.cnki.jvs.2014.08.010
