行走激励的傅里叶级数模型及其参数的实验研究

陈 隽， 王浩祺， 彭怡欣,2

(1.同济大学，上海 200092；2.香港理工大学，香港 红磡)

行走激励的傅里叶级数模型及其参数的实验研究

陈 隽1， 王浩祺1， 彭怡欣1,2

(1.同济大学，上海 200092；2.香港理工大学，香港 红磡)

利用三维动作捕捉技术结合三向测力板，开展了7种不同步行频率下行走激励的动力特性实验，得到73人次5 004条有效单足落步荷载曲线。利用实测的双足重合的准确时间点将单足落步荷载曲线拓展成连续时程曲线，进而得到行走激励竖向及横向分量的傅里叶级数模型的前5阶系数及相位角值。与其它国家现有模型的比较反映出了不同人群特性的差异，所建议模型可用于大跨工程结构考虑行走作用的振动舒适度问题的设计与分析。

行走激励；傅里叶级数模型；三维动作捕捉；动载因子

伴随高强轻质材料的广泛应用以及设计方法的进步，大跨度楼盖、大跨(人行)桥、长悬臂型结构、空中连廊、超长楼梯等结构型式在工程实践中日趋流行。由于自振频率降低及结构阻尼减少，这些结构在使用者的步行、跳跃、跑动或舞蹈等活动下会产生竖向或水平振动，严重时会引起结构上其他使用者的不安甚至恐慌，形成人致结构振动的舒适度问题[1-3]，也是大跨结构设计中必须认真考虑的控制性因素。

可靠的荷载模型是保障结构分析准确性的大前提。然而对于人致激励如步行、跳跃等，国内目前尚没有相应的荷载模型或取值标准。工程设计与计算分析中只能选用国外的激励模型，如美国AISC[4]、英国CSTR43[5]、SCI-P354[6]、IABSE[7]等规范建议的模型，或者Blanchard等[8], Bachmann等[9], Kerr[10], Young[11], Petersen等[12]众多学者在不同时期所提出的模型。不同模型间参数取值差别很大，除去早期实验研究设备精度较差的原因外，不同国家成年人人体体征参数(身高、体重、体段质心与惯性矩等)的显著差异是另一个重要原因，并且已经得到国内外运动医学等相关学科研究成果的证明[13-15]。因此，开展针对中国人行走特点的行走激励动力特性的实验与工程分析模型研究显得十分迫切和必要。

为此，本文采用三维步态分析技术结合固定测力板，开展了73人次不同步频下步行荷载特性的实验测试工作，共得到5 004条有效单足落步荷载曲线，为目前文献中最多的记录。利用周期性对单足落步荷载曲线拓展后得到连续时程曲线，并进而建议了行走激励竖向与水平向分量的傅里叶级数模型中的参数与相位角取值。

1 实验步骤与结果

1.1 实验装置

本研究实验场所及装置布置如图1(a)所示，包括10个红外摄像机(Vicon T40型)、两块高精度三维测力板(美国AMTI OR6-7型)和一块2.1米长的足底压力测试板(RSSCAN-Footscan型)。以上所有设备集成在Vicon步态分析测试系统，可实现同步测试与控制。

图1 实验室环境及测试者Fig.1 Experimental Setup and participant with markers

三维步态分析技术利用高速摄像机捕捉安装在运动主体特征点处的若干反光标记物(称为Marker点，参见图1(b))的三维运动轨迹。利用此技术，可在行走激励测试中记录实验者的运动状态，从而可准确定义试验者行走的速度、步距以及双足重合时间等重要参数。此外，实验室空间大小以及测力板前后放置的安排都充分考虑到了测试者能够在实验中采取舒适自然的步态，保证测得的步行力时程数据的可靠性。此前，国内尚未有采用三维步态分析技术研究行走激励的公开报道。

1.2 实验步骤

已完成73名测试者的步行荷载实验(59名男性及14名女性)，皆为健康成年人，基本信息如表1所示。按照医学常用标准，测试者在实验中共安装有39个Marker点，如图1(b)所示。

每位测试者共完成了7组步行工况的实验，包括三组慢速、中速、快速的自选速度以及四组固定行走频率为1.5、1.75、2.0和2.25 Hz的步行实验。测试者行走方向如图1(a)中箭头所示，即图中y方向为行走方向，x方向垂直于步行方向且平行于人体左右方向，z方向为垂直于测力板方向。每组工况重复6-7次，并确保每个工况能采集到有效数据(即两足分别完整地踏在两块测力板上)。固定频率步行以电子节拍器发出固定节拍的单音短响声引导，测试者根据声响踏节拍点步行。每完成一组测试工况，转入下一组工况时，均给予测试者一定时间作预演适应。详细的实验测点安装、测试步骤与实验过程的描述见文献[16]。

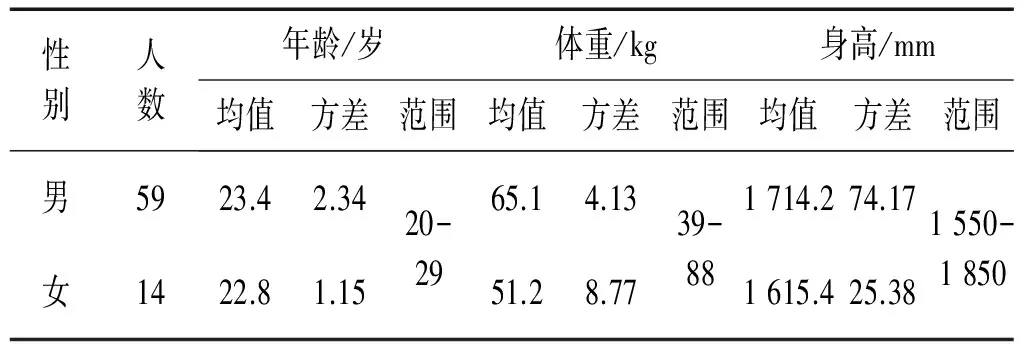
表1 测试者统计数据

1.3 实验结果

目前已完成73人次的行走激励实验，每组测试数据包括39个Marker点的轨迹，两块测力板上的单足落步荷载曲线，足底压力板数据以及录像资料。经数据质量检验，共得到5 004组有效单足落步荷载曲线时程记录，各工况有效记录情况见表2所示。

表2 各工况有效数据数量统计

Tab.2 Statistics of valid data for each condition

工况自由步行∗固定频率步行/HzSNF1．51．752．02．25N∗725691683738736720711

*S，N和F分别表示慢速、中速、快速；N为各工况的有效数据数量

图2(a)-(b)分别为某女性测试者(身高：1 670 mm，体重50 kg)在中速自由行走工况以及2.0 Hz固定频率行走工况下，三维测力台所记录的行走激励三个分量Fx,Fy和Fz的时程。各分量方向的定义见图1(a)。图中实线表示两个三维测力台的合力，虚线表示两个测力台分别录得的单足落步荷载曲线。

图2 典型实测结果Fig.2 Typical measurements of walking load

2 行走激励的模型

2.1 傅里叶级数模型

行走激励的竖向及水平侧向分量的荷载模型，对于大跨楼盖以及大跨度行人桥等振动舒适度分析具有重要的工程价值。假设步行过程是以单足落步荷载曲线为周期的重复过程，即忽略左右足的差别，将单足落步荷载曲线反复循环，则竖向Fz(t)及侧向Fx(t)连续步行荷载在时域上可以表达为傅里叶级数的形式：

(1)

(2)

其中Fz(t)和Fx(t)分别为竖向和侧向行走激励；G为人的静止重力；αzi和αxi分别为竖向和侧向第i阶傅里叶系数，也常称为动载因子(Dynamic Loading Factor/DLF);fp为人的步行频率；φzi和φxi分别为竖向和侧向第i阶谐波相位角；n为模型中考虑的阶数。

傅里叶级数模型是现有的行走激励模型研究中最为常见的一种。以此模型为基础，许多研究者对动载因子DLF的取值作了研究。这种模型引入单步周期性假设，通过对单足落步荷载曲线按一定规律进行拓展叠加求得连续时程曲线。对此，文献[17]研究了由实测荷载曲线拓展连续时程曲线的方法。由于本实验的动作捕捉技术已经记录到了第二步落足的时间点，因此可以准确地将单足落步曲线拓展为连续的时程曲线，从而获得DLF值及其相位角。

2.2 动载因子取值

利用实验所得单足落步荷载曲线以及下一步的落足时间，首先将单步落足曲线拓展为连续曲线(文中取30步长度)。进行归一化处理后(即除以人体体重)，再求曲线的傅里叶幅值谱，对应步频及其倍频处的谱值即为动载因子。典型连续时程曲线及其傅里叶幅值谱见图3。按照上述步骤计算出了所有5 004条有效记录的前五阶DLF值，图4(a)-(e)给出了计算所得竖向前五阶动载因子随步频的变化。

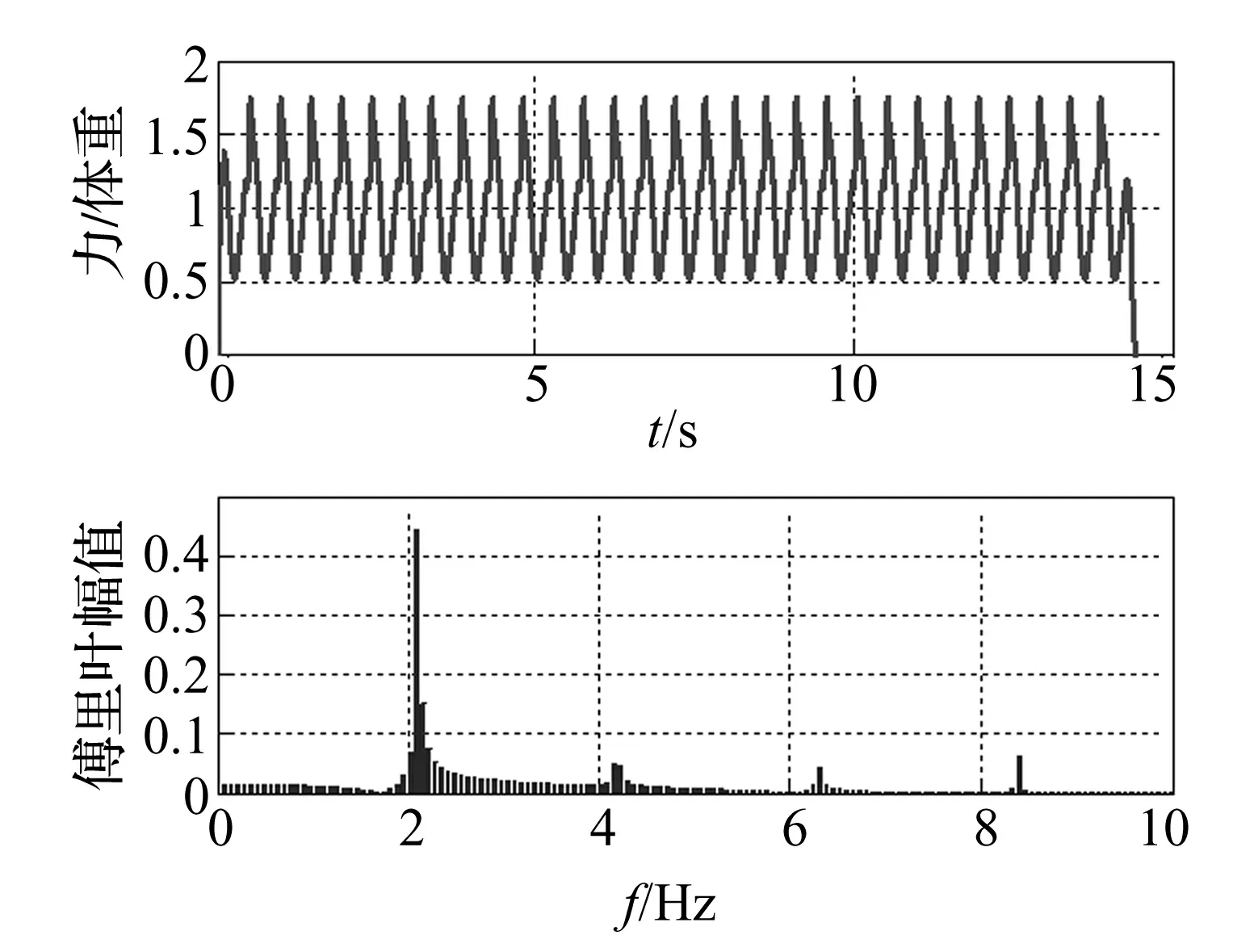
图3 典型连续时程曲线及其傅里叶幅值谱Fig.3 Typical continuous time history and its Fourier spectrum

根据本文实验计算得的各阶动载因子的均值示于表3。图4给出了实验所得的竖向第一阶动载因子的分布规律。由图看出，z方向动载因子比较离散，且大致呈现对数正态分布，高阶动载因子规律与此基本相同。考虑使DLF取值具有一定的保证率，得到的各阶动载因子设计值列于表4(75%保证率情况)，式中fp为行走频率。

图4 第一阶动载因子概率密度图Fig.4 Probability density of first DLF

阶数z方向x方向10．2358fp-0．26110．041320．07570．019930．0409/40．0355/50．0261/

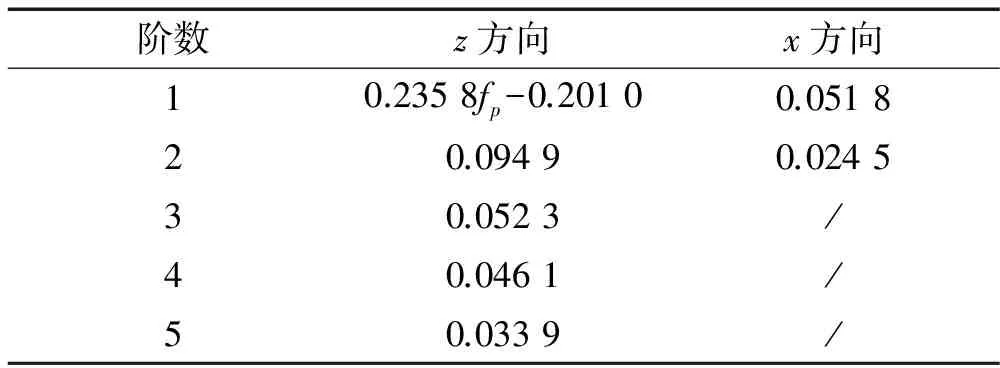
表4 各阶动载因子设计值

2.3 相位角取值

数据显示，无论竖向还是横向分量其相位角的实验结果非常离散，与国外已有研究的实验现象相同。因此，根据实验数据统计给出竖向及侧向各阶相位角的建议取值如下：对z方向，第一、四、五阶相位角值分别取-π/4、π/4、π/2；对x方向，第一阶相位角取π/3，其余各阶相位角均取0。

3 所建议模型与现有国外步行荷载模型的比较

选取五种国外研究者所提出的步行荷载模型与本文模型进行比较，表5列出了不同模型所建议的竖向分量的动载因子。需要指出，由于上述模型的实验方法(测力板、单足落步荷载曲线拓展方式等)以及其系数是均值还是一定保证率下的设计值都不是非常明确，因此以下比较并不十分严格。这也从一个侧面说明了实验方法及测试人群特性的差异以及对行走激励模型的影响。

五种模型中以Kerr[10]的博士论文的实验研究最具有代表性，是英国规范以及Young[11]和 Zivanovic等[18]后续研究的基础。Kerr共测试了882条单足落步荷载曲线，本研究的样本数量远高于此。

图5(a)-(e)给出了本文实验的竖向DLF结果与其他模型对比。从图5(a)可以看出，其他模型第一阶动载因子大多略高于本文提出的均值。Kerr模型[10]的第一阶动载在高步频段有一个明显的下降段，此后Young[11]将此段修正为平台段。本文实验中大部分测试者表示步频高于2.25 Hz后较难保持自然的行走步态(表现为大于2.25 Hz的DLF值非常离散)。同时，自由步行工况中，步频高于2.25 Hz的数据量甚少，也说明高步频步行运动在自然步行状态下出现频率较低。

图5 不同模型各阶动载因子比较Fig.5 Comparison of DLFs from different models for each order

年份研究者动载因子步频/Hz1977Blanchard等[8]αz1=0．257/1987Bachmann与Ammann[9]αz1=0．37，αz2=0．10，αz3=0．12，αz4=0．04，αz5=0．0821997AISC模型[4]αz1=0．5，αz2=0．2，αz3=0．1，αz4=0．051．6-8．81999Kerr等[10]αz1为步频的三次函数，αv2=0．07/2000Young[11]αz1=0．41(fp-0．95)≤0．56αz2=0．069+0．0056fαz3=0．033+0．0064fαz4=0．013+0．0065f1-2．82005Petersen[12]αz1=0．073，αz2=0．138，αz3=0．018αz1=0．408，αz2=0．079，αz3=0．018αz1=0．518，αz2=0．058，αz3=0．0411．52．02．52007Zivanovic[18]αz1与αz2同Kerr[16]αz3=αz4=0．05αz5=0．03/2013本文αz1=0．2358f-0．2010αz2=0．0949αz3=0．0523αz4=0．0461αz5=0．03391．2-3

图6 不同模型连续时程曲线比较Fig.6 Comparison of DLFs from different models for each order

图5(b)-(e)表示不同模型高阶动载因子的比较。第二阶及第三阶动载因子除Pertersen模型[12]及Young模型[11]外，其他模型均取常数。Young 模型[11]共取4阶谐波，第二阶至第四阶动载因子都是关于步频斜率接近0的直线。Kerr模型[10]取前4阶谐波，Zivanovic等[18]将其发展至前5阶。除AISC模型[4]外，其他模型的高阶动载因子均与本文均值吻合较好，并低于本文设计值。

由不同研究者提出的步行荷载傅里叶级数模型确定的连续时程曲线对比示于图6。计算时取步频为2 Hz，假定行走者体重为700 N，可见曲线的峰值大小有一定的差异。

4 结 论

利用新颖的三维动作捕捉技术结合测力板开展了针对中国人行走特点的行走激励动力特性系列实验。利用实验获得的5 004条单足落步曲线并基于傅里叶技术模型，提出了连续行走激励的竖向与水平向分量的动载因子和相位角取值建议，可供工程设计与分析参考使用。

[ 1 ] 折雄雄，陈隽.大跨度楼盖振动舒适度研究综述[J].结构工程师，2009，25(6)：144-149. SHE Xiong-xiong, CHEN Jun. A review of vibration serviceability for long-span floors[J]. Structural Engineers, 2009, 25(6): 144-149.

[ 2 ] 樊健生，李泉，李全旺，等. 考虑人-结构相互作用的楼盖振动控制研究[J]. 振动与冲击，2010,29(11)：230-236. FAN Jian-sheng, LI Quan, LI Quan-wang, et al. Investigation on the control of floor vibration considering the interact of people and structures[J]. Journal of Vibration and Shock, 2010,29(11):230-236.

[ 3 ] 简方梁，吴定俊，李奇. 上海虹桥车站人行走廊人致振动分析[J]. 振动与冲击，2010,29(8)：136-140. JIAN Fang-liang, WU Ding-jun, LI Qi. Human-induced vibration analysis of the footbridge in Shanghai Hongqiao railway station[J]. Journal of Vibration and Shock, 2010, 29(8):136-140.

[ 4 ] Murray T M, Allen D E, Ungar E E. Floor vibrations due to human activity[S].Steel Design Guide 11. American Institute of Steel Construction, 1997.

[ 5 ] The Concrete Society. Concrete Society Technical Report 43: Second Edition, Appendix G[S]. 2005.

[ 6 ] The Steel Construction Institute. SCI P354, design of floors for vibration: a new approach[S]. 2007.

[ 7 ] Matsumoto Y，Nishioka T，Shiojiri H，et al. Dynamic design of footbridges[C]. IABSE Proceedings．1978：17-78．

[ 8 ] Blanchard J, Davies B L, Smith J W. Design criteria and analysis for dynamic loading of footbridges[C]. Symposium on Dynamic Behaviour of Bridges at the Transport and Road Research Laboratory, Crowthorne, Berkshire, England, May 19,1977:96-106.

[ 9 ] Bachmann H, Ammann W. Vibrations in structures: Induced by man and machines[M]. Iabse, 1987.

[10] Kerr S C. Human induced loading on staircases[D]. University of London, 1998.

[11] Young P. Improved floor vibration prediction methodologies[C]. Arup Vibration Seminar, 2001.

[12] Blanco C M, Bouillard P, Bodarwé E, et al. Structural dynamic design of a footbridge under pedestrian loading[C]. 9th SAMTECH Users Conference. 2005.

[13] 毛松华，李瑶章，侯曼. 中国男青年人体惯性参数的实测研究[J]. 北京体育大学学报，1999，3：56-58. MAO Song-hua, LI Yao-zhang, HOU Man. Study of inertia parameters of human body in chinese male youngsters[J]. Journal of Beijing University of Physical Education, 1999,3:56-58.

[14] 夏长丽，石岫昆，孟祥辉，等. 计算中国女性青年人体惯性参数的数学模型及其回归方程[J]. 解剖学杂志, 1999,22(5):452-454. XIA Chang-li, SHI Xiu-kun，MENG Xiang-hui，et al. Study of mathematical model and trinal regression equation for calculating inertial parameters of chinese female young bodies[J]. Chinese Journal of Anatomy, 1999,22(5): 452-454.

[15] 王明鑫，俞光荣，王中琴，等. 正常中国成年人足底压力分析[J]. 中国矫形外科杂志, 2008,16(9): 687-690. WANG Ming-xin, YU Guang-rong, WANG Zhong-qin, et al. Analysis of plantar pressure distribution of the normal Chinese adult[J]. Orthopedic Journal of China, 2008,16(9): 687-690.

[16] 彭怡欣. 基于三维步态分析技术的步行荷载实验建模研究[D]. 上海：同济大学，2012.

[17] 陈隽，叶艇，彭怡欣. 拓展步行荷载对楼板振动响应影响的对比研究[J]. 振动与冲击，2012, 31(18)：55-59. CHEN Jun, YE Ting, PENG Yi-xin. A comparison study on methods for expanding a single foot-falling load curve based on floor responses[J]. Journal of Vibration and Shock, 2012, 31(18):55-59.

[18] Zivanovic S, Pavic A, Reynolds P. Probability-based prediction of multi-mode vibration response to walking excitation[J]. Engineering Structures, 2007, 29(6): 942-954.

Experimental investigation on Fourier-series model of walking load and its coefficients

CHEN Jun1，WANG Hao-qi1，PENG Yi-xin1,2

(1.Tongji University, Shanghai 200092，China；2. The Hong Kong Polytechnic University, Hung Hom, Hong Kong, China)

Using a three-dimensional human motion capture system and three-dimensional force plates, a series of experiments on dynamic properties of human-induced walking load with seven different walking frequencies were conducted. 73 persons participated in the experiments to acquire 5 004 record curves of single-footfall trace. The continuous time history of walking load was synthesized with single-step force curves by using the measured correct time points for two-fool-reclosing. Based on experimental measurements, the coefficients and phase angles of the first five orders of Fourier-series models for both vertical and lateral walking load components were achieved. Comparing this model with existing models of other countries, the difference among different nations’ characteristics were reflected. The proposed model could be used for structural design and analysis of long-span structures considering the problems of serviceability caused by human walking.

human walking load; Fourier series model; 3D motion capture; dynamic load factor

国家自然科学基金(51178338);上海市自然科学基金(11ZR1439800)

2013-05-03 修改稿收到日期：2013-06-21

陈隽 男，博士，教授，博导，1972年4月生

TU312+.1

A

10.13465/j.cnki.jvs.2014.08.003