基于有限差分法的工作辊弯辊挠曲计算
2014-08-10严国平
严国平
(中冶南方工程技术有限公司技术研究院 湖北武汉430223)
·设计与研究·
基于有限差分法的工作辊弯辊挠曲计算
严国平
(中冶南方工程技术有限公司技术研究院 湖北武汉430223)
以弯曲变形的微分方程为理论基础,运用有限差分法相关原理对这些微分方程进行了相关推导,得出了一定弯辊力作用下工作辊挠曲变形计算的线性方程组表达式。通过给定的计算实例,编制了相关计算程序,完成了一定弯辊力作用下某工作辊的挠曲变形计算。结果表明:在较大弯辊力作用下,工作辊沿x轴正向各截面的挠曲呈非线性变大趋势,且在弯辊轴承中心作用点处达到最大。此外,有限差分法不失为一种快速有效地求解工作辊多点挠度的计算方法。
有限差分法 工作辊 挠曲变形 程序求解
1 引言
工作辊是轧机辊系装配中的重要组成部分,它直接与带钢接触并在一定的轧制力下完成对带钢的轧制,工作时其通过一定的弯辊作用对轧制板形进行调节。因此,工作辊的强度与刚度的大小将直接对轧机的板形控制能力产生影响。故在进行轧机工作辊设计时,需对其工作时的挠度进行计算。
文献[1]结合Singularity函数与Laplace变换给合的方法给出了阶梯梁弯曲变形的表达式,文献[2]采用阶跃函数与拉氏变换对阶梯梁弯曲变形的表达式进行详细的推导,并结合书写规则给出了主体计算代码。文献[3]利用奇异函数对阶梯轴的弯曲变形进行了求解,并给出了求解示例。文献[4]应用固定端法结合某一实例对阶梯轴的变形进行了计算演绎。但是这些方法都较为复杂,对不同安装方式都需要进行重新推导,不利于标准化设计,且推导都具有一定的难度,不利于实际工程设计应用。
采用有限差分法对工作辊挠度进行了计算。该法是一种数值分析方法,它将求解微分方程的问题转化为求解代数方程组的问题,通过定义的边界即可以迅速完成特定轴系的求解,具有较强的可操作性。
2 工作辊挠度计算的数学模型
根据轧机工作机制及工作辊受力特点,建立工作辊挠度计算的力学模型,如图1所示。

图1 工作辊挠度计算的力学模型
图1中,以工作辊中心截面为固定支撑面,以轴承中心D点为弯辊力所在位置。OA段为工作辊实际工作段直径d1,对应长度为l1,AB段为轴承座密封段直径d2,对应长度为l2,BC段为过渡轴段直径d3,对应长度为l3,CD段为工作辊轴承座对应安装轴承段直径d4,对应长度为l4。建立如图1所示坐标系xoy,将工作辊轴向划分成n等分,并给每个节点(每个节点代表一个截面)分别进行编号,从左至右为1,2,3,…,n。每个节点之间的间隔均为h,以向右方向为x轴正向。
对于任意截面,该截面的弯矩、转角与挠度的关系可以用以下微分方程[5]表示:
(1)
式中yi—截面xi对应的轴心的挠度值;M(xi)—截面xi对应的弯矩值;E—工作辊材料的弹性模量;I(xi)—截面xi对应的截面惯性矩,与截面的轴径有关;
θ(xi)—截面xi对应的转角。
根据差分原则:
(2)
转化后即有:
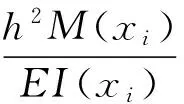
(3)
则有方程组:
(4)
由边界条件知:
(5)
则解得:
(6)
组成AX=b的非线性齐次方程组即可有相应的矩阵表达式,如式(7)所示:
(7)
式(7)为一个三对角线性方程组,将系数矩阵求逆矩阵后,与右侧的矩阵进行相乘,然后通过编制相应的计算求解程序,即可求得相应的工作辊挠度曲线。
3 具体计算实例
某工作辊挠度计算所需参数如表1所示。

表1 某工作辊参数表
结合图1所示的计算力学模型,并代入表1中相关参数至(1)~(7)中,建立计算矩阵方程有:

(8)
根据式(8)编制相关的有限差分法计算程序,计算结果如下。
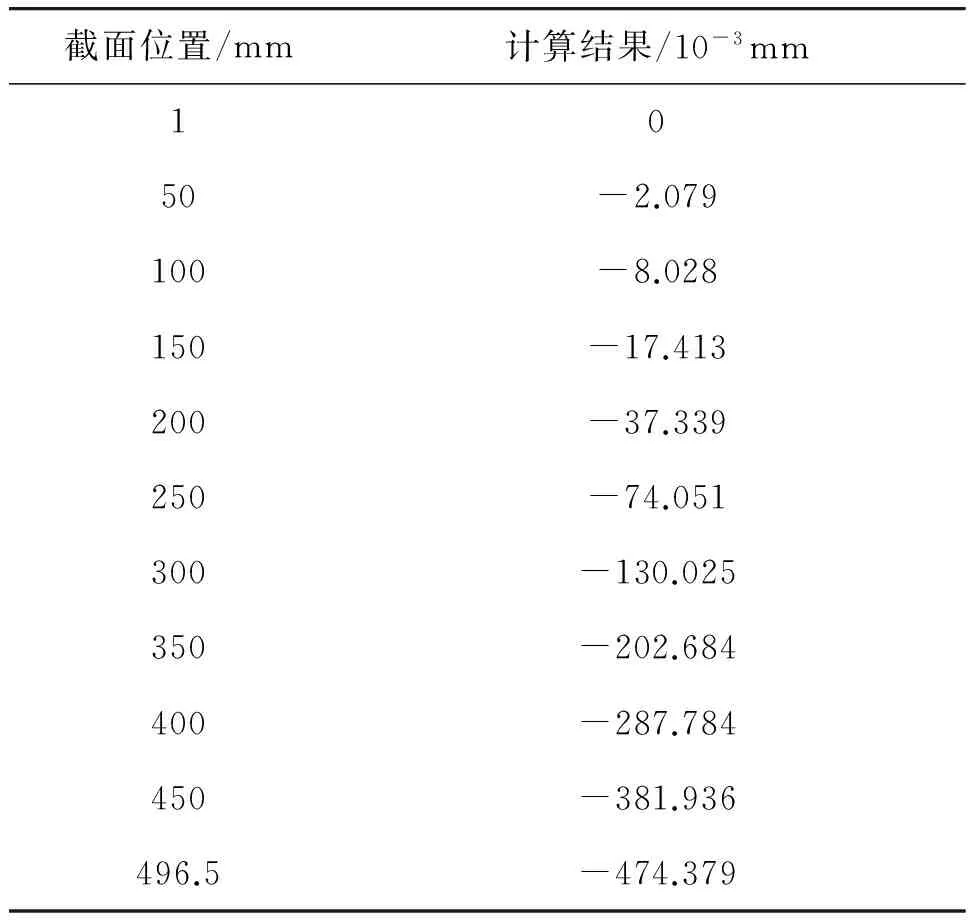
表2 截面计算挠度
从计算结果可以看到:沿着坐标x正向方向,各截面挠曲逐渐变大,这种变化趋势呈非线性变化,在最外侧在弯辊轴承中心作用点处挠曲值达到最大,最大值为0.474mm。这说明,在较大弯辊力作用下,工作辊轴承段的变形较大,在进行实际设计过程中,应该将工作辊的变形计算考虑至板形控制系统中,从而使轧机板形控制能力达到合理范围。

图2 工作辊弯辊的挠度曲线
4 结论
通过以上分析,可以得到如下结论:
1)在较大弯辊力作用下,工作辊沿x轴正向各截面的挠曲呈非线性变大趋势,且在弯辊轴承中心作用点处达到最大。实际设计过程中,应考虑与轧机的板形控制相结合,以期能使弯辊效果达到理想状态。
2)有限差分法是一种数值分析方法,通过差分方式可以快速有效地求得工作辊多点的挠度,这个能全面地反映工作辊沿x正向的弯曲变形情况,这对于类似的设计都具有沿用与借鉴意义,也为高度的程序化设计与计算提供了便利。
[1]陈连,王元文.阶梯梁弯曲变形的普遍表达式及其应用[J].机械强度,2000,Vol.22(2):153-155.
[2]刘传芬.阶梯轴弯曲变形的通解及其应用[J].机械设计与制造,1993(3):37-39.
[3]王燮山.利用奇异函数求解阶梯轴的弯曲变形[J].机械强度,1983(3):80-85.
[4]林成厚,郭华北.应用固定端法计算阶梯轴(梁)的变形[J].山东科学,1996,Vol.9(4):26-29.
[5]刘鸿文.材料力学[M].北京:高等教育出版社,2000.
Calculation of Bending Rigidity for the Working Roll Based on Finite Difference Method
Yang Guoping
(WISDRI Engineering & Research Incorporation Limited, Wuhan 430223)
Based on the differential equations of bending deformation, the linear equations for the working roll deformation with the effect of a certain bending force was expressed by means of finite difference method. Through one given example, the corresponding calculation program was carried out for the working roll deformation. The results show that each section deflection along the positive x axis has the nonlinear changing trend with the effect of larger bending force. The deformation maximum exits on the loaded bearing center point. In addition, finite difference method is also rapid and effective for some similar solving problems.
Finite difference method Working roll Bending rigidity Programmed solution
严国平,1978年出生,毕业于武汉理工大学,工学博士,主要从事冶金设备的研发、机械系统设计与数值仿真研究
TG333.17
A
10.3969/j.issn.1001-1269.2014.04.001
2014-03-18)
