带有不确定性的异步中立时滞系统的鲁棒镇定
2014-08-08孟建梅
孟建梅
(晋中职业技术学院,山西 晋中 030600)
带有不确定性的异步中立时滞系统的鲁棒镇定
孟建梅
(晋中职业技术学院,山西 晋中 030600)
研究一类基于异步切换的带有不确定性的中立时滞系统的鲁棒控制镇定问题.通过构造不同的Lyapunov泛函,基于平均驻留时间得到了闭环系统指数稳定的的充分条件,然后给出系统鲁棒镇定的控制器设计方法。
异步切换; 中立时滞系统; 平均驻留时间;不确定性
1、引言
中立时滞系统作为一种特殊的时滞系统,它不仅在系统的状态中考虑了时滞,在系统状态的导数中也考虑了时滞,这就使得对这种系统的研究比通常的时滞系统更加复杂和困难,同时这也使得中立时滞系统有着更广泛的实际应用背景。
近几十年来,关于中立时滞系统也有了很多的研究成果,如带有时滞的系统稳定性分析[1-3],带有不确定性的系统鲁棒控制[4,5]及稳定性分析[6,7],这表明中立时滞系统不仅得到了越来越多人的关注与研究,这同时也说明了中立时滞系统的在实际生活中的逐渐增加的实际性与应用性。
在实际的系统中,由于系统时滞的存在性及系统需要时间来辨识哪个子系统在运行以及将要实施哪个与之相匹配的子控制器,这将导致控制器和系统模态之间的异步切换的产生。文献[6]基于平均驻留时间方法研究了切换线性系统的异步切换控制,文献[7]研究了在离散情形下切换系统的异步H∞滤波。然而,据作者所知,关于带有不确定性的异步切换的中立时滞系统的鲁棒镇定问题还未进行研究,而这就促发了本文的研究。本文将基于平均驻留时间研究一类基于异步切换的带有不确定性的中立时滞系统的鲁棒控制镇定问题。

2.1 问题描述及知识预备
考虑如下的切换中立时滞系统
(1)

ΔAi,ΔCi是具有适当维数的不确定性系统矩阵,且满足[ΔAiΔCi]=EiFi[U1iU2i]
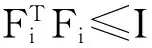
由于在实际操作中需要时间来辨识被激活子系统以及实施相匹配的子控制器,这将导致控制器和系统模态之间的异步切换。 因此,我们设计如下的动态输出反馈控制器:u(t)=Kσ(t-Δ)x(t)
(2)

其中Δk
应用(2)于系统(1),由于时滞的存在,当第i个子系统切换到第j个子系统时,滞后Δi的控制器Ki仍在运行,则异步切换下最终的闭环系统为:
(3)
其中

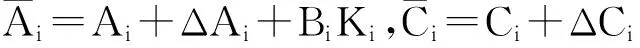
(4)
目的就是通过合理的设计一个控制器,使得闭环系统(3)是指数稳定的。


2.2 稳定性及镇定性分析
本节将给出系统的稳定性及镇定性分析,以及切换系统的基于平均驻留时间方法的异步切换控制器的设计方法。
定理1:对于给定的正常数α和β,如果存在具有适当维数的对称矩阵Pi,Ri,Rij使
(5)
(6)
Pi<μ1Pj,Pj<μ2Pi,Ri<μ1Rij,Rij<μ2Ri
(7)
证明:当t∈[tk+Δk,tk+1),系统和控制器都位于第i个模态。选取Lyapunov泛函为:

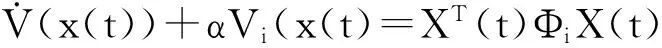

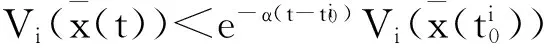
(8)
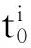
当t∈[tk+1,tk+1+Δk+1),系统位于第j个子系统,控制器仍处于第i个模态.选取Lyapunov泛函为:

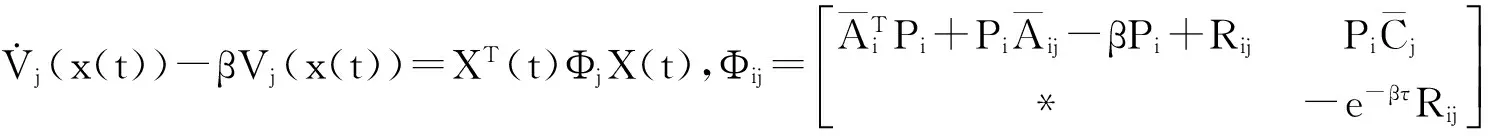

(9)

用t0,t1,…,tk表示在区间[t0,t)上的切换时刻,考虑下面闭环系统的分段Lyapunov泛函
由(7),(8)和(9)可知,对于t≥tk+Δk,有V(t)<…<(μ1μ2)ke-αT-(t0,t)+βT+(t0,t)V(t0)

V(t) (10) (11) (12) 其中 且Si<μ1Sj,Sj<μ2Si,Ni<μ1Nij,Nij<μ2Ni. (14) 则存在正数εi使得(14)等价于 (15) 由Schur补可知(15)等价于(11) 同理,可得(6)等价于(12)。 因此,如果LMIs(11)、(12)成立,则最终的闭环系统(3)是指数稳定的,且所满足的控制器增益通过定理给出。 研究了一类带有不确定性的中立时滞系统的异步切换鲁棒控制。通过构造不同的Lyapunov泛函,基于平均驻留时间得到了系统指数稳定的充分条件,以线性矩阵不等式的形式给出控制器鲁棒镇定的设计方法。 [1]DanZhang,LiYu.Exponential stability analysis for neutral switched systems with interval time-varying mixed delays and nonlinear perturbations[J].Nonlinear Analysis:Hybrid Systems,2012 6:775-786. [2]Jinfeng Gao,Hongye Su,Xiaofu Ji,Jian Chu.Stability analysis for a class of neutral systems with mixed delays and sector-bounded nonlinearity[J].Nonlinear Analysis: Real World Applications,2008,9:2350-2360. [3]Xin-Ge Liu,Min Wu,Ralph Martin,Mei-Lan Tang .Stability analysis for neutral systems with mixed delays[J].Journal of Computational and Applied Mathematics,2007,202:478-497. [4]王降,黄敏.不确定时变时滞中立型系统的鲁棒 H∞控制[J].江南大学学报(自然科学版),2008,7(6):641-646. [5]焦建民.一类不确定中立型系统的鲁棒稳定性分析[J].山东大学学报(理学版),2011,46(1):28-34. [6]Duyu Liu,Shouming Zhong,Xinzhi Liu,Yuanqing Huang.Stability analysis for uncertain switched neutral systems withdiscrete time-varying delay: A delay-dependent method[J].Mathematics and Computers in Simulation,2009,80: 436-448. [7]Chang HuaLien,Ker WeiYu,Yeong JayChung,Yen FengLin,Long YeuChung,Jenq DerChen.Exponential stability analysis for uncertain switched neutral systems with interval-time-varying state delay[J].Nonlinear Analysis: Hybrid Systems,2009,3:334-342. [8]Xin-Ge Liu,Min Wu,Ralph Martin,Mei-Lan Tang.Delay-dependent stability analysis for uncertain neutral systems with time-varying delays[J].Mathematics and Computers in Simulation,2007,75:15-27. (责任编辑:孙强) Robust Stabilization for a Class of Switched Neutral Systems with Uncertainty MENG Jian-mei (Jinzhong Vocationa & Technical College,Jinzhong,Shanxi 030600,China) The problem of robust control stabilization for a class of switched neutral systems with uncertainty is considered based on asynchronous switching.Through constructing different Lyapunov functional,a sufficient condition for the exponential stability of the closed-loop systems is developed for switched neutral systems by the average dwell time method,the controller design method which made the system robust stabilization is given. asynchronous switching;neutral delay system;average dwell time 2013-09-01 孟建梅(1982-),女,山西文水人,助教,硕士。 TH161 A 1671-4385(2014)02-0115-04


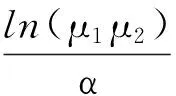

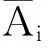
3 小结
