基于ARMA 模型的接收机钟差短期预测

梁愈高， 田克纯

(桂林电子科技大学研究生院 桂林 541004)

基于ARMA 模型的接收机钟差短期预测

梁愈高， 田克纯

(桂林电子科技大学研究生院 桂林 541004)

接收机钟差预测在辅助信号的快速捕获、辅助定位解算和接收机自主完好性监测等领域具有实际的应用意义。详细介绍ARMA模型建模的一般方法，对实测的钟差数据进行ARMA模型的建模和预测，算例结果表明：建立的ARMA模型具有较好的短期预测效果。

ARMA模型； 接收机钟差； 钟差预测

引 言

接收机钟差是接收机时钟与导航系统时钟两者之间的偏差，通过求解定位定时方程组可以解算出接收机的三维坐标和接收机钟差。当接收机的时钟频率保持稳定时，可以根据历史钟差数据建立模型并预测后续一段时间的钟差数据。接收机钟差预测能够缩小码相位的不确定范围，减小信号搜索范围，有效辅助信号的快速捕获[1]，另外，接收机钟差预测在恶劣环境下辅助接收机定位解算[2]与接收机自主完好性监测[3]等领域也有广泛应用。因此，对接收机钟差进行建模与预测具有实际应用意义。

常用的接收机钟差模型有二次多项式模型和灰色模型[4]。二次多项式模型预报的钟差误差随着时间推移有明显的累积效应，因而适用于短期的钟差预报。灰色模型使用较少的钟差数据建模，提高了建模速度，且灰色模型的短期预报精度与二次多项式模型基本相当，具有一定的优越性。但是，这两种常用模型主要是对钟差的趋势项进行建模，而没有考虑钟差的随机项。由于钟差数据经过差分处理后可以得到平稳的时间序列，因此本文利用时间序列分析理论对钟差数据进行分析，在介绍ARMA建模的一般方法的基础上，通过实测的接收机钟差数据进行建模和预测。对实验结果的分析表明，本文建立的ARMA模型在短期预测中具有比较理想的预测精度。

1 ARMA模型原理

ARMA(Autoregression and Moving Average)系列模型是研究时间序列的有效手段[5]。ARMA系列模型主要包括自回归AR(Autoregression)模型、滑动平均MA(Moving Average)模型以及自回归滑动平均ARMA模型。

ARMA(p，q)模型[6]的一般表达式为：

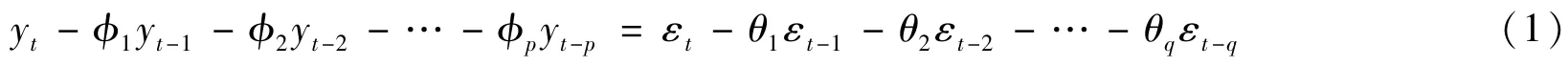
根据时间序列分析理论，用ARMA模型建模的时间序列要求为平稳时间序列，而原始的接收机钟差序列往往呈现一定的趋势或者周期特征[7]，不能直接用ARMA模型建模，因此要通过对原始钟差序列进行差分运算消除趋势性和周期性，使其变成平稳的时间序列，然后再进行ARMA模型建模。

2 ARMA模型的建立

2.1 模型的识别与定阶

模型的识别主要是根据时间序列样本的自相关函数和偏相关函数的特征来判断时间序列是AR(p)模型、MA(q)模型或者ARMA(p，q)模型。设y1，y2，…，yN是来自平稳时间序列{yt}的一个样本，¯y为样本均值，则样本的自协方差为：

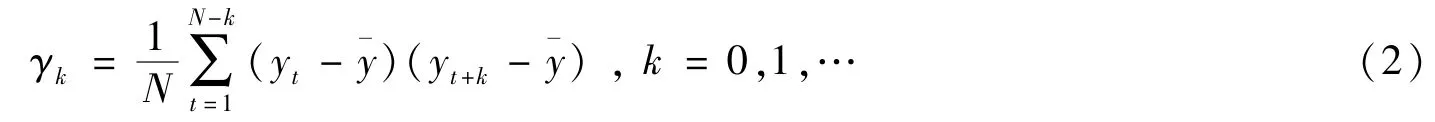
对应的样本自相关函数为：

样本的偏相关函数计算公式为：

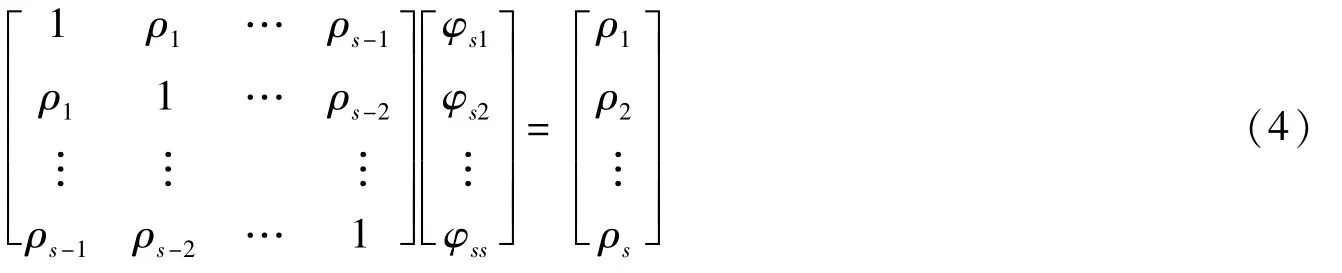
将样本的自相关函数代入式(4)，依次取s＝1，2，…，分别解出φ11，φ22，…，φss，即可得到偏相关函数的估计量。理论上平稳AR、MA和ARMA模型的自相关和偏相关函数特征如表1所示。

表1 平稳时间序列自相关和偏相关函数特征

模型的定阶[8]过程是通过考察平稳时间序列样本自相关函数和偏相关函数的性质选择合适的模型拟合观测值序列，估计自相关阶数p和滑动平均阶数q，而要获得比较准确的ARMA模型阶数通常使用BIC准则：

其中，k＝p+q为模型的阶数，σ2为残差方差，N为采用的序列长度。选择不同的p和q，对原始数据进行拟合并计算相应的BIC值，使得BIC(k)取最小值的k0即是最佳的模型阶数。

2.2 模型的参数估计

经过初步识别时间序列可能适应的模型类型后，接着对模型的参数φ1，φ2，…，φp和θ1，θ2，…，θq进行估计。本文采用矩估计法，即用样本的估计量代 替γs、ρs，从γs或者ρs与模型参数的关系中解出模型参数的估计值。ARMA(p，q)模型参数矩估计[9]计算步骤如下：

①估计自回归系数φ1，φ2，…，φp

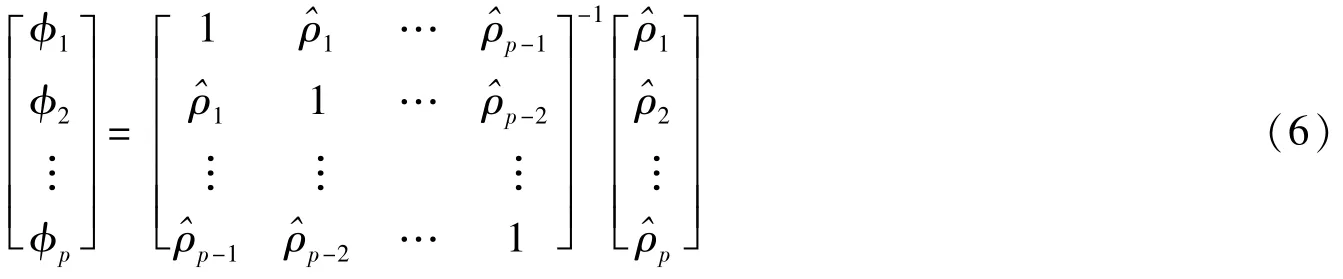
②对模型做变换，令y′t＝yt-(φ1yt-1+φ2yt-2+…+φpyt-p)，则

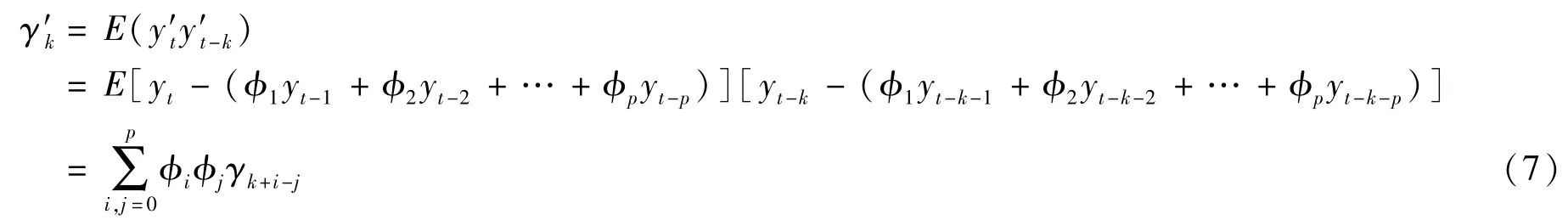
这里，φi、φj可由第①步计算得到。

③由第②步模型的变换有y′t＝εt-θ1εt-1-…-θqεt-q，则γ′k＝σ2(-θk+θ1θk+1+…+θq-kθq)， k＝0，1，…

将第②步得到的γ′代入上式，即可得到关于θ1，θ2，…，θq的非线性方程组，解非线性方程组估计出θ1，θ2，…，θq。

2.3 模型的检验

当建立的模型为ARMA(p，q)时，利用估计出的模型参数可以计算出模型的残差序列，递推关系如下：

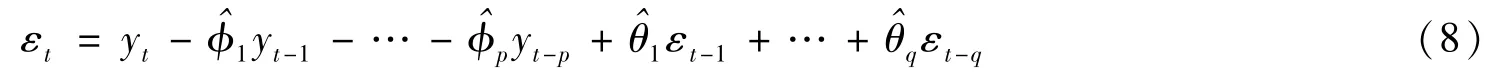
取εt＝0和yt＝0(t＜0)即可得到模型残差的样本序列ε1，ε2，…εN。

根据Box和Pierce(1970)提出的残差序列白噪声检验的统计量：

其中，ρs(ε)为残差序列的自相关函数。当ε1，ε2，…εN来自白噪声序列时，Qm渐进服从自由度为(m-pq)的χ2分布。

检验的零假设是残差序列不存在自相关，即：H0：ρ1(ε)＝ρ2(ε)＝…＝ρm(ε)＝0。

3 算例与分析

算例选取IGS提供的BJFS测站从2014年3月4日至2014年3月8日五天的接收机钟差数据进行建模和预测，其中取2014年3月4日的数据用于建模，然后用模型预测未来四天的钟差变化，并将模型的预测值和实际的测量值对比分析。2014年3月4日的钟差数据如图1所示，具有一定的趋势和周期特征，不满足ARMA模型建模对时间序列的平稳性要求[10]。本文通过差分运算把原始的接收机钟差数据变成平稳的时间序列，如图2所示。经过差分运算后原始数据的趋势和周期性得到了很好的消除，根据式(3)和式(4)计算差分后序列的自相关函数和偏相关函数如图3、图4所示。

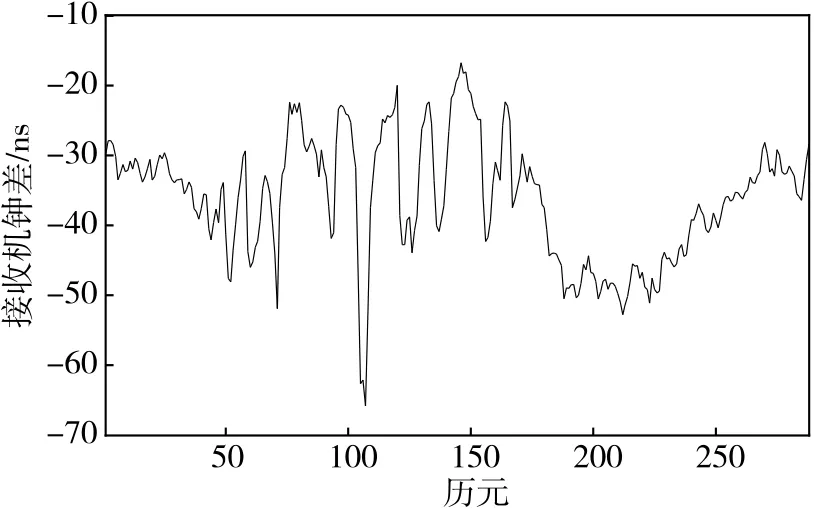
图1 接收机钟差原始数据

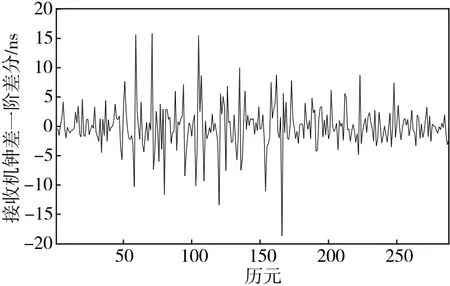
图2 接收机钟差的一阶差分

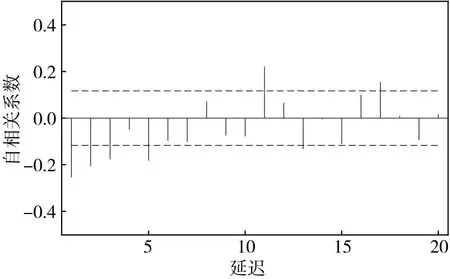
图3 自相关图

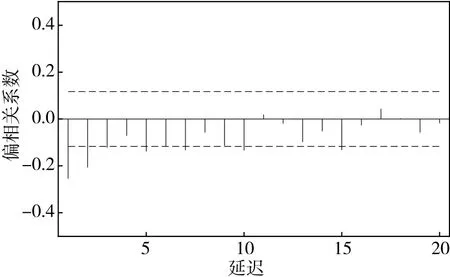
图4 偏相关图

由自相关图和偏相关图可以看出，延迟16阶仍然具有较强的相关性，可以判定为自相关和偏相关表现拖尾的性质。初步判断模型的阶数后，通过BIC准则最终确定模型为ARMA(2，2)。最后利用建立的模型预测2014年3月5日至3月8日四天的钟差变化，并将预测值和原始数据值之间的差值列于表2中，对应的预测值和原始数据值之间的差值分布如图5所示。

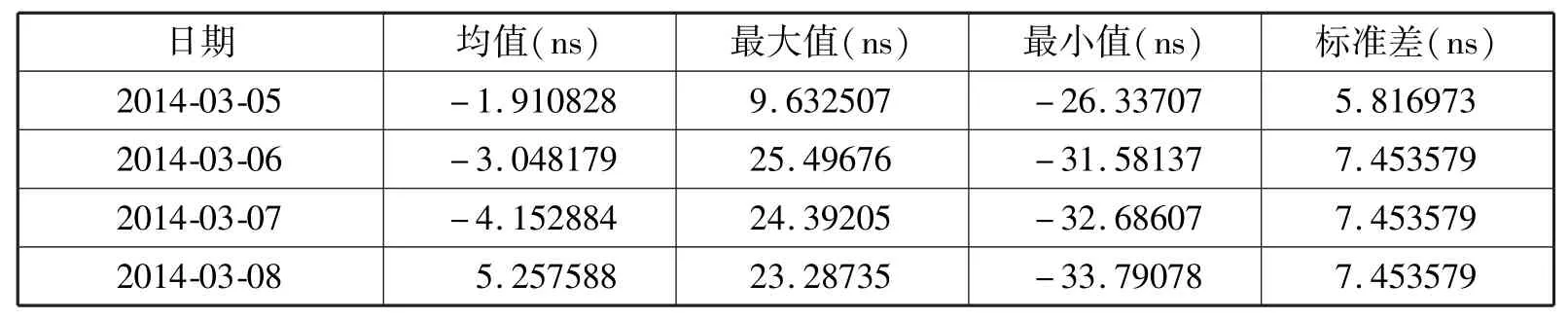
表2 预测值与原始数据的差值统计

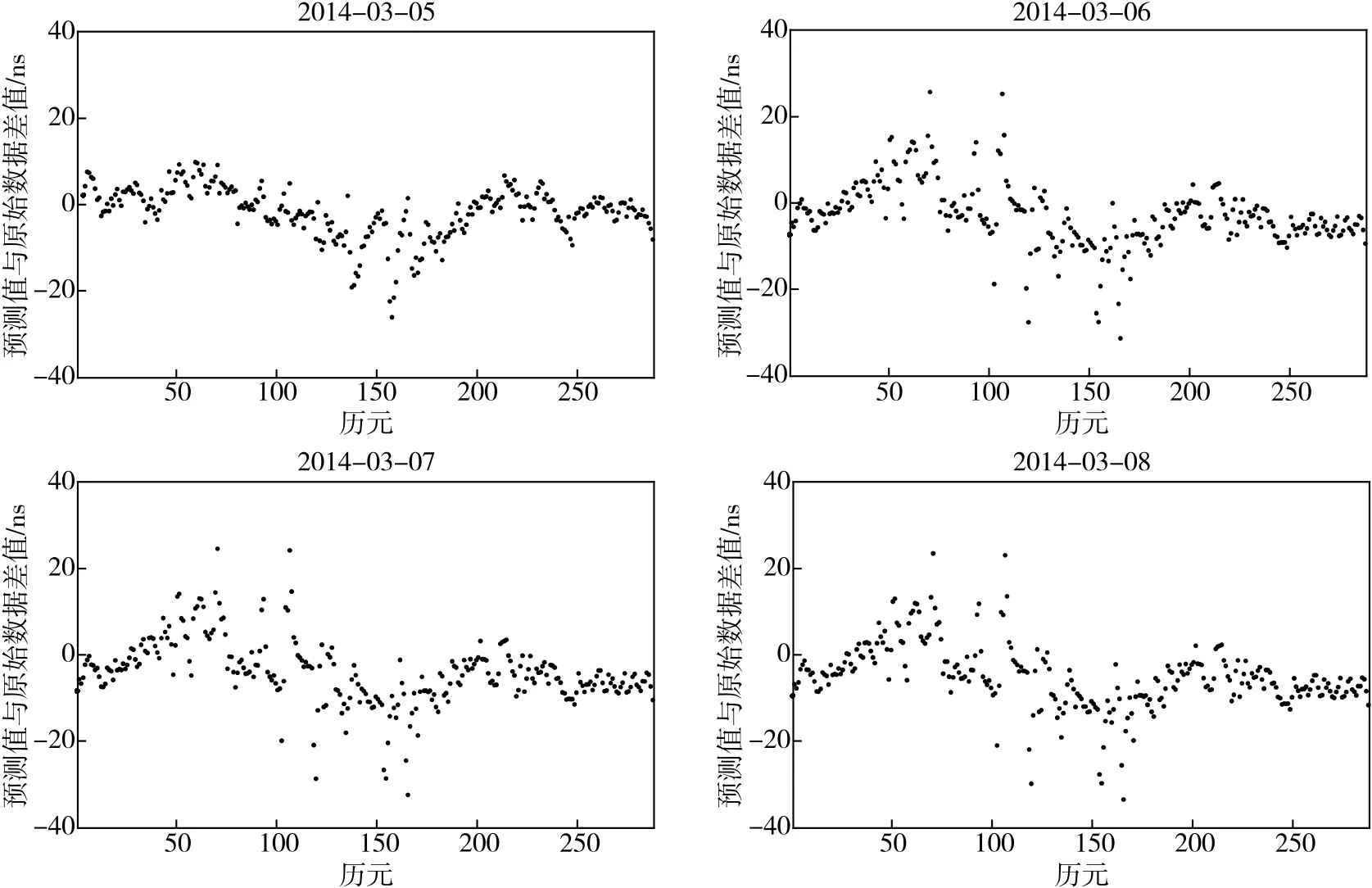
图5 ARMA模型预测值与原始数据差值分布

通过算例分析和模型预测值与原始数据差值统计表及差值分布图可以得出：

①采用ARMA模型分析接收机钟差数据，首先要判断原始钟差数据的平稳性，如果原始钟差数据不是平稳序列，则需要预先对原始钟差数据作平稳化处理才能进行ARMA模型建模。

②由差值统计表可以看出，连续四天的预测值与原始数据差值的均值都在6ns以内，说明建立的ARMA模型预测精度可以满足要求。

③随着预测天数的增加，预测值与原始数据偏差的均值逐渐增大，预测值的精度逐渐变差。因此，预测值的精度在短期预测中相对较高。

④表2中，随着预测天数的增加，最大值和最小值整体偏移，均值逐渐增大而标准差保持不变，是由于ARMA模型预测误差具有一定的累积效应，预测值有一定的偏离趋势。若要进行更长天数的预测还应当对ARMA模型作改进。

4 与相关模型比较

为了评估本文建立的ARMA模型预测效果，采用相同的数据建立二次多项式模型和灰色模型，并将这三种模型的预测效果进行比较。2014年3月5日至3月8日连续四天预测值与原始数据的差值统计示于表3，差值分布如图6所示。由差值统计表和分布图可以得出以下结论：

①ARMA模型预测差值整体平稳，而灰色模型和二次多项式模型预测差值波动比较大。相比另外两种模型，ARMA模型预测值拟合原始数据值的精度较高。

②图6中，三种模型在200个历元以内的预测误差基本相同。但是，随着时间的延长，灰色模型和二次多项式模型的预测误差均呈现出不同程度的累积效应。在实际应用中，使用ARMA模型可以获得更高的预测精度。

③二次多项式模型的预测误差具有明显的累积效应，随着预测时长的增加，预测误差越来越大，甚至有可能超过钟差本身的量级，说明二次多项式模型只适合于很短时间的预测。

表3 连续四天预测值与原始数据的差值统计

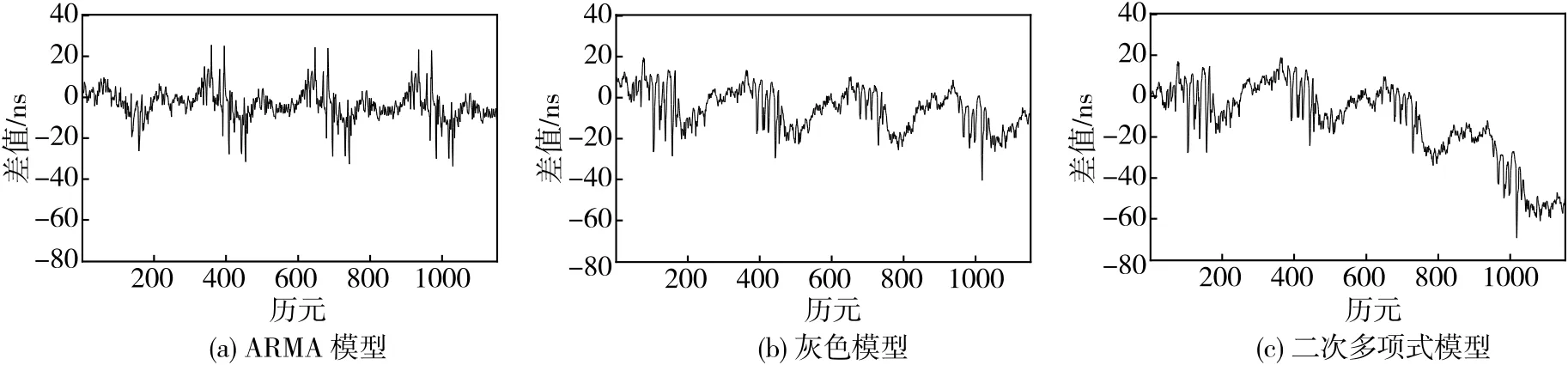
图6 三种模型预测差值分布

5 结束语

本文在介绍ARMA模型原理的基础上，详细说明了ARMA模型的识别和定阶、参数估计以及模型的检验，并用实测的接收机钟差数据进行建模，然后进行短期预测，分析表明建立的ARMA模型预测精度基本满足要求，在短期预测中具有较好的预测效果。本文还将ARMA模型与常用的两种预测模型进行了比较，进一步说明了ARMA模型在接收机钟差预测中的优越性。

[1] 王梦丽，许晓勇，王飞雪.接收机温启动状态下辅助长码快捕的钟差预测算法[J].测绘科学，2008，33(S3)：129～131.

[2] 滕云龙.GPS接收机数据处理技术研究[D].成都：电子科技大学，2011.

[3] 许龙霞，李孝辉.基于接收机钟差的GPS完好性自主检测算法[J].宇航学报，2011，32(3)：537～542.

[4] 陈 安，吴 鹏，等.短期接收机钟差预测方法及性能分析[J].全球定位系统，2013，38(4)：11～15.

[5] 陈 军.GPS接收机单向授时算法研究[D].郑州：解放军信息工程大学，2010.

[6] 史代敏，谢小燕.应用时间序列分析[M].北京：高等教育出版社，2011.

[7] 李 辉，李 隆，乔建新.基于AR模型的GPS授时分析[J].测绘技术装备，2012，14(1)：25～26.

[8] 李晓宇，杨 洋，胡晓粉，贾蕊溪.基于改进灰色ARMA模型的卫星钟差短期预报研究[J].大地测量与地球动力学，2013，33(1)：59～63.

[9] 徐文令，侯旻峡，谭 聪，崔景顺.ARMA模型的模型识别和参数估计研究[J].电源技术应用，2013，(5)：307～308.

[10] 徐君毅，曾安敏.ARIMA(0，2，q)模型在卫星钟差预报中的应用[J].大地测量与地球动力学，2009，29(5)：116～120.

Short-term Receiver Clock Bias Prediction Based on ARMA M odel

Liang Yugao， Tian Kechun

The receiver clock bias prediction has the particularly practical application value on the fast acquisition，positioning calculation of auxiliary signal and the receiver autonomous integrity monitoring.The method of ARMA modeling is described in detail，and the ARMA model is used for clock bias prediction with the actual clock biasmeasurement data.The results show that the ARMA model is valid for the short-term receiver clock bias prediction.

ARMA model； Receiver clock bias； Clock bias prediction

P228.4

A

CN11-1780(2014)05-0042-05

梁愈高 1988年生，硕士，研究方向为卫星导航定位定时技术。

2014-06-17 收修改稿日期：2014-07-07

田克纯 1950年生，教授，硕士生导师，研究方向为无线电通信技术。