一种改进的全球卫星导航系统多星故障排除方法∗

侯 冰， 张晓林， 郭九源

(北京航空航天大学电子信息工程学院 北京 100191)

一种改进的全球卫星导航系统多星故障排除方法∗

侯 冰， 张晓林， 郭九源

(北京航空航天大学电子信息工程学院 北京 100191)

分析全球卫星导航系统的多星故障排除方法，研究跳出传统模式的接收机自主完好性监测算法——随机搜索法，针对其不足之处，在奇偶矢量法的基础上研究了检测门限和排故率的关系，提出一种新的检测门限选取方法，平衡了漏检率和虚警率，明显提高了随机搜索法的整体排故率，尤其是在可见卫星数较少、故障偏差较小的情况下，排故率的提升更为显著。同时，改进算法的运算量相对于奇偶矢量法仅小幅上升。仿真实验表明，改进算法有效可行，适用于全球卫星导航系统中的多星故障排除。

接收机自主完好性监测； 多星故障排除； 检测门限选取； 随机搜索法

引 言

在卫星导航系统中，完好性异常是指不可预测的超过工作容差的距离误差，通常由卫星或控制段引起，且这种异常发生的概率很低，一般每年仅发生几次[1]，但若不加以排除，可能会导致定位精度的急剧恶化。当卫星导航接收机作为唯一导航设备时，尤其需要考虑完好性的问题，除了要向用户提供定位、授时及导航功能之外，还必须具备完好性监测功能。

接收机自主完好性监测(RAIM)是利用冗余观测信息对卫星测量值进行一致性检验的技术，在定位误差超过允许限值时，系统及时向用户发出告警。目前关于RAIM的算法大多适用于单星故障检测和排除，如奇偶矢量法[2]和最优奇偶矢量法[3]。然而随着GPS、北斗卫星导航系统、GLONASS和Galileo等卫星导航系统的发展，多系统组合导航已成趋势。随着可用于定位的卫星星座的增多，两颗甚至多颗卫星同时发生故障的概率将不能再被忽略，在进行RAIM算法研究中应予以考虑。

本文在分析现有的多星故障排除RAIM算法的基础上，对其中排故性能较好的随机搜索法进行进一步的研究和分析，针对其不足之处提出一种改进算法，提高了算法的整体性能。

1 随机搜索法

目前针对多星故障的RAIM算法主要有以下几种。分组法是一种既可以用于单星故障排除又可以用于多星故障排除的基础算法，该算法排故率高，但是运算量很大，而且在实际情况下，由于故障卫星数量未知，算法的性能会受到很大的影响[4]。Ni Junjie等[5]提出了改进最小二乘残差法用于多星故障处理，改进算法在一次迭代中可以识别两颗故障卫星，充分利用了下一代GNSS的高冗余度，通过牺牲一些正确测量值来识别故障。卢虎等[6]提出了一种新型故障卫星分离方法，考虑到北斗系统可见卫星数较少的特点，将两种奇偶相关方法和传统的分组法结合起来，虽排故率略低于分组法，但所耗时间较少。Jin Hong等[7，8]提出了一种针对特定传感器故障进行诊断的最优奇偶矢量法，然而仿真结果表明该方法运算复杂且故障识别率过低[9，10]。张强等[9～12]提出了一种多星故障识别方法，称为“假设验证法”，在故障较小(如4σ0)时，识别率有待进一步提高。Zhang Yun[13]等提出一种新的多星故障排除方法，可逐个增加预计故障卫星数，通过在每一步中逐个调低观测卫星权重并估计最小二乘总残差进行故障识别，这种方法的运算量与分组法类似。

以上可用于多星故障排除的算法的故障排除模式都是相同的，都是先通过某种方式识别出故障卫星，然后排除故障卫星以获得无故障星座。陈灿辉[14]提出一种随机搜索法RSM(Random Search Method)，利用了故障检测率比故障排除率高的特点，跳出了传统“故障识别-排除故障星-得到无故障星座”的模式，从搜索所有可见星得到含有最多无故障卫星星座的角度来实现故障排除的目的，并能获得较高的故障排除率。图1所示是RSM的排故流程图。

图1 随机搜索法排故流程

RSM算法主要过程如下[14]：

①编码：将观测卫星组合方案用二进制串编码方式表示。将每颗卫星设为一个二进制字码，数字1表示该卫星被选入，数字0表示该卫星未选入。对所有可见卫星按顺序进行编排，最低位表示第1号卫星。

②随机初始化：以随机的方式产生一个长度等于总观测卫星数n的二进制整数。由于故障检测的要求，随机二进制数中1的个数应不小于m+ 1，m是用户位置和钟差矢量增量的维数，单系统m＝4，双系统m＝5。为满足排故需要，二进制整数中1的个数也不应大于n-1。考虑到多星故障排除的需要，在观测卫星数足够多的情况下，该二进制数中1的个数以不大于n-3为宜，即假定最多可能同时存在3颗故障星。随机产生的二进制整数就对应了一种卫星组合方案。采用故障检测函数对这个卫星组合方案进行检测，若故障检测通过，则初始化工作完成。否则，继续进行初始化，直至所产生的卫星组合方案无故障。

③搜索排故：搜索排故的过程就是以②中得到的初始化无故障星座为基础，用故障检测函数，在初始无故障星座中逐步增加未选卫星，最终获得含有最多无故障卫星的星座。具体操作方式为：按先后顺序依次检测对应星座组合方案的二进制整数中的字码，若检测字码为1，则继续检测下一字码。否则，将该字码变为1，得到一种新的组合方案，利用故障检测函数对该方案进行检测。如果故障检测通过，则该字码保持为1，否则将该字码恢复为0，再继续检测下一字码。所有字码都检测完成时，就可将最终得到的二进制整数对应的星座组合方案视为含有最多无故障卫星的星座，从而完成故障排除。

由于RSM算法是以故障检测为基础来进行的，因而其故障排除率会受故障检测方法的影响。表1和表2分别给出了故障检测方法为奇偶矢量法和最优奇偶矢量法时RSM的故障排除率。其中，pbias为使漏检概率等于容许漏检率的偏差值的临界偏差，有[1]：pbias＝λσ0。λ为非中心χ2分布密度函数的非中心参数，σ0是伪距测量误差标准差。

为方便叙述，本文把故障检测方法为奇偶矢量法和最优奇偶矢量法的RSM分别简称为PRSM(parity vectormethod RSM)和ORSM(optimal parity vectormethod RSM)。

表1 PRSM的故障排除率(%)

表2 ORSM的故障排除率(%)

根据文献[14]的仿真结果，在单星故障排除方面，PRSM排故性能和奇偶矢量法相当，而ORSM排故性能和最优奇偶矢量法相当。在多星故障检测与排除方面，PRSM的排故性能明显优于其他算法，ORSM的排故性能则更好。

2 改进的RSM算法

2.1 RSM算法的不足之处

故障检测方法分别为奇偶矢量法和最优奇偶矢量法时，RSM算法的运算时间如表3和表4所示。由表中数据可见，RSM算法的运算时间总体上随故障大小和故障卫星数量的增大而减小，随可见卫星数量增大而增大。两个表格数据对比可见，ORSM的运算时间至少为PRSM的2.5倍，最多可能达到其27倍以上。而且显然随着可见卫星数的增多，运算时间的差距逐渐增大。

表3 PRSM的运算时间(ms)

表4 ORSM的运算时间(ms)

在当前多系统联合导航的趋势下，可见星数量越来越多，这也就导致将RSM应用于多星故障排除时，ORSM反应时间会很长。虽然PRSM的运行时间相对较短，且随可见卫星数量的增多运行时间增长较为缓慢，但其排故率不尽如人意。因此，亟待寻找一种新的故障检测方法，以期在较短的运行时间内获得较好的排故性能。

2.2 门限选取

本节首先介绍奇偶矢量法的门限选取方法[10]。在采用线性化方法进行导航定位求解时，可将观测方程描述为：

其中，y表示伪距预测值与测量值之差，y∈Rn，n为可见卫星数；Δx表示由用户位置和接收机钟差的增量组成的矢量，称为状态量增量，Δx∈Rm，m表示未知量个数，m＝3+nsys，nsys表示卫星系统个数；H是Δx和y之间的线性关联矩阵，也称为方向余弦矩阵，H∈Rn×m；ε为伪距测量误差矢量。

通过方向余弦矩阵H的QR分解来获得奇偶矩阵，进而得到奇偶矢量。设

式中，Q为正交矩阵，Q∈Rn×n；R∈Rn×m，有

式中，Rx为上三角阵，Rx∈Rm×m。令

其中，Qx∈Rm×n，Qp∈R(n-m)×n。因为Q为正交阵，故有：

从而，Qp为奇偶空间矩阵，其性质为：各行相互正交，大小归一，并与H的各列相互正交。定义奇偶矢量p如下：

根据式(1)并利用QpH＝0的性质，可得

在奇偶矢量法中采用pTp作为检验统计量，可用FSSE来表示pTp，即

作二元假设：

在无卫星故障时，检测结果应正常，若出现告警信息，则为虚警。给定虚警概率PFA，根据上面的分析，可根据式(10)确定门限值TD。

根据TD可确定统计量＾σ所对应的检测门限σT：

表1的仿真实验证明，根据上述方法确定的检测门限TD导致了较大的漏检率，整体排故率有待进一步提高。本文将从检测门限选择方法入手，试图提高RSM的排故性能。

检测门限的选择受到多方面因素的影响，其中主要考虑的参数是虚警率与漏检率[15]。由虚警率与漏检率关系可知，增大检测门限，对应的虚警率减小，漏检率增大；减小检测门限，虚警率增大，漏检率减小。可见，虚警率和漏检率是一对相互矛盾的指标，不能同时降低。

由于RSM算法主要是基于故障检测方法完成排故，因而降低漏检率不仅可使排故前的故障检测率提高，而且能提高故障排除过程中的故障检测算法性能，从而提高排故率。但另一方面，虚警率的提高不仅表现在系统无故障时，故障检测报告有故障；还会在故障排除过程中，误将无故障卫星判断为有故障，不加入无故障卫星组合中，从而导致算法性能的降低。

为了有效降低奇偶矢量法的漏检率，进而提高RSM算法的排故率，本文首先引入调整系数K[4]，将实际的检测门限改为：T′D＝TD×K，且0＜K≤1。由于随着故障量级的增大，漏检率降低[16]，因此本文在故障偏差较小(0.8pbias)的情况下针对K取不同值的双星故障排除率进行了仿真，结果如表5所示。

表5 故障偏差0.8pbias情况下K取不同值的PRSM双星故障排除率(%)

从表5中可以看出，随着K值下降，排故率首先呈上升趋势，这主要是由于门限值的降低导致漏检率的降低，使得故障排除过程中的故障检测算法性能有所提高，从而使得排故率显著提高。但当K值降低到一定值后，排故率出现下降趋势。这主要是由于门限值过低，使得虚警率上升，导致在故障排除的过程中将无故障卫星判断为有故障而不加入无故障卫星组合中，从而致使排故率降低。换言之，也就是虚警率提升带来的性能下降会逐渐抵消掉漏检率下降带来的性能提升。因此，我们需要找到最优门限值，使RSM算法达到最佳性能。

从表5中我们还可以发现最优门限值和观测卫星数之间的关系，即每一列中最高排故率对应的K值随着观测卫星数的增加而增大，并且呈线性关系。这是因为随着卫星的增多，卫星伪距中的随机噪声的增多削弱了故障对系统的影响，使系统对故障检测不敏感，造成漏检率上升，因而最优门限值也随之上升。

根据以上仿真结果和分析，我们提出取K＝0.5+(nsl-13)×0.025，可以使PRSM算法性能达到最优，其中nsl为观测卫星数。本文下一节将对此进行进一步仿真验证。

3 仿真实验

为了对本文改进算法与RSM算法进行性能对比，本文设置与参考文献[14]相同的仿真条件，即以北斗卫星导航系统和GPS双系统为参考，分别以检测与排除1颗、2颗和3颗故障卫星为例进行仿真实验验证。采用含有北斗卫星系统和GPS的导航信号模拟器作为信号源来产生卫星信号，并以随机选取故障卫星的方式施加相应的故障大小，观测卫星数分别设置为13、15、17、19、21、23六种情形，并采用Monte Carlo方法进行仿真，每种情形均进行了一万次仿真实验。而在故障检测函数中，参考国际民间航空组织(ICAO)对导航性能的要求[17]，设定虚警率PFA为10-5/h，漏检率PMD为0.001。对伪距测量误差的标准差σ0，参考文献[18]的相应参数，取为6m。施加的故障大小以临界偏差pbias作为参考。仿真结果如表6、表7所示。

为了更清晰对比改进前后RSM算法性能的变化，将表6分别与表1和表2的数值相减，得到图2和图3。

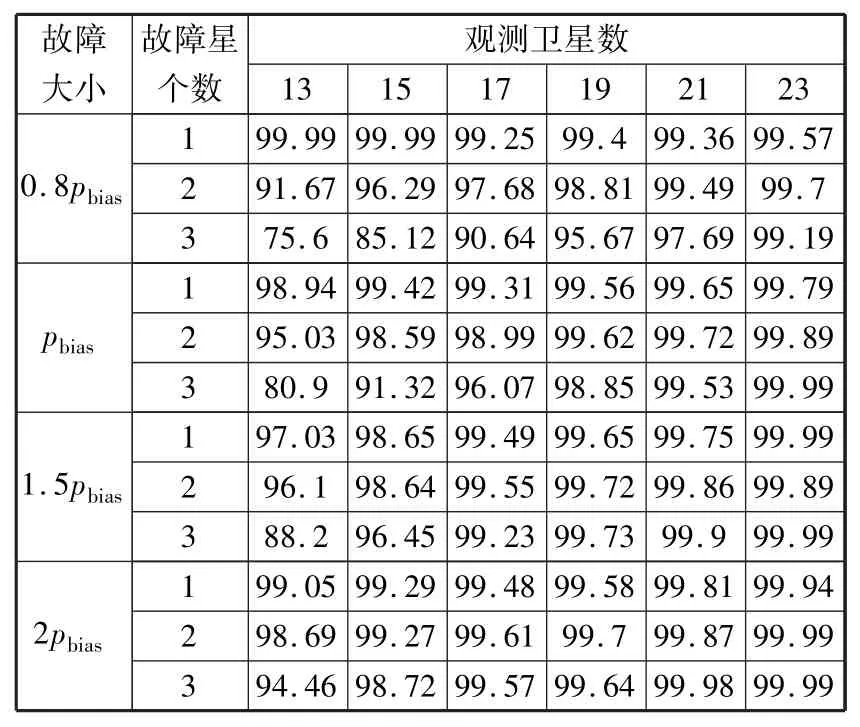
表6 改进的RSM的故障排除率(%)

表7 改进的RSM的运算时间(ms)

图2 相对PRSM改进的RSM排故率的提高

图3 相对ORSM改进的RSM排故率的提高

从图2和图3可以看出，改进的RSM排故率性能总体上有明显提升，尤其在可视卫星数少、故障较小时，改进故障检测方法的RSM的性能甚至优于ORSM。在故障大小为0.8pbias的双星故障条件下，改进RSM的排故率较PRSM和ORSM分别提高了46.05和31.67个百分点。而在可见卫星数多、故障偏差大时，改进RSM的排故率与RSM基本持平。此外，改进RSM的故障排除率对于故障数的变化更加稳定，这有利于故障卫星数未知时的多星故障排除。

在运算时间方面，改进的RSM运算时间和PRSM处于同一量级，在可见卫星数少、故障较小时其运算时间略高于PRSM，但是仍远远小于ORSM。因此，改进的RSM算法综合性能更加优越。

4 结束语

本文研究了非传统模式的RAIM算法——随机搜索法，针对其两种故障检测方法——奇偶矢量法和最优奇偶矢量法分别具有排故率不高和运算量大的缺点，在奇偶矢量法的基础上提出一种新的检测门限选取方法，明显提高了随机搜索法的整体排故率，尤其是在可见卫星数较少、故障较小的情况下，排故率的提升更为显著。同时，改进算法的整体运算量较奇偶矢量法仅小幅上升，仍远小于最优奇偶矢量法。因此，本文改进算法的整体性能更为优越，是卫星导航系统中用于多星故障排除的简单有效的方法。

[1] Elliott Kaplan.GPS原理与应用(第二版)[M].寇艳红，译.北京：电子工业出版社，2007.

[2] Ahmed IA，Li C，Tan Z Z.The Study of RAIM Performance by Simulation[J].CADDM，2006，16(2)：58～64.

[3] 杨 静，张洪钺.卫星故障诊断的最优奇偶向量法[J].航空学报，2002，23(2)：183～186.

[4] 程思天.卫星导航接收机自主完好性监测方法的研究与实现[D].北京：北京航空航天大学，2012.

[5] Ni Junjie，Zhu Yongxin，Guo Wei.An Improved RAIM Scheme for Processing Multiple Outliers in GNSS[C].21st International Conference on Advanced Information Networking and ApplicationsWorkshops(AINAW'07)，2007：840～845.

[6] 卢 虎，廉 杰.北斗用户机自主完好性监测研究[J].空军工程大学学报(自然科学版)，2010，11(3)：53～57.

[7] Jin Hong，Zhang Hongyue.Failure Detection Using Optimal Parity Vector Sensitive to Special Sensor Failure[C]. Proceedings of the 1996 IEEE/SICE/RSJ International Conference on Multisensor Fusion and Integration for Intelligent Systems，1996：55～61.

[8] Jin Hong，Zhang Hongyue.Optimal Parity Vector Sensitive to Designated Sensor Fault[J].IEEE Transactions on Aerospace and Electronic Systems，1999，35(4)：1122～1128.

[9] 张 强，张晓林，常啸鸣.用于卫星导航多星故障识别的新方法[J].航空学报，2008，29(5)：1239～1244.

[10] 张 强.GPS和BD2双模接收机基带结构及解算软件技术研究[D].北京航空航天大学，2010.

[11] Zhang Qiang，Zhang Xiaolin，Chang Xiaoming.Research on RAIM Algorithm under the Assumption of Simultaneous Multiple Satellites Failure[C].Eighth ACIS International Conference on Software Engineering，Artificial Intelligence，Networking，and Parallel/Distributed Computing，2007：719～724.

[12] 张晓林，张 强，常啸鸣，等.基于多星故障识别的GNSS接收机自主完整性监测方法：中国.ZL200610165465.8 [P].2007-7-11.

[13] Zhang Yun，Wu Falin，IsshikiH.New Cascade Method for Detecting GPSMultiple Outliers Based on Total Residuals of Observation Equations[C].Position Location and Navigation Symposium(PLANS)，2012 IEEE/ION，2012：208～215.

[14] 陈灿辉，张晓林.全球导航卫星系统多星故障排除新方法[J].北京航空航天大学学报，2011，37(12)：1479～1483.

[15] Salos D，Martineau A，Macabiau C，Bonhoure B，Kubrak D.Receiver Autonomous Integrity Monitoring of GNSS Signals for Electronic Toll Collection[J].IEEE Transactions on Intelligent Transportation Systems，2014，15(1)：94～103.

[16] 彭兴钊，黄国荣，郭 创，程洪炳.奇偶矢量RAIM算法的故障检测研究[J].弹箭与制导学报，2011，31(6)：199～202.

[17] Feng Shaojun，Washington Y Ochieng，David Walsh，et al.A Measurement Domain Receiver Autonomous Integrity Monitoring Algorithm[J].GPSSolution，2006，10(2)：85～96.

[18] Pratap Misra，Per Enge.全球定位系统——信号、测量与性能(第二版)[M].罗鸣，等，译.北京：电子工业出版社，2008.

An Im proved M ethod of M ulti-satellite Faults Exclusion for GNSS

Hou Bing， Zhang Xiaolin， Guo Jiuyuan

Methods of multi-satellite faults exclusion for GNSS are analyzed，and an unconventional receiver autonomous integritymonitoring(RAIM)algorithm called random searchmethod(RSM)is studied.For the shortcomings of RSM，the relationship between the detection threshold and fault exclusion rate is studied based on the parity vectormethod.A novelmethod of detection threshold selection is proposed to raise the fault exclusion rate by balancing the missing detection rate and false alarm rate，especially on the conditions of little visible satellites and small fault bias.Meanwhile，the computation of the improved method just increases slightly compared with the parity vectormethod.Simulation results show that the improvedmethod is effective and feasible to themulti-satellite faults exclusion for GNSS.

RAIM； Multi-satellite faults exclusion； Detection threshold selection； Random Search Method

TN967.1

A

CN11-1780(2014)05-0023-07

侯 冰 1986年生，在读博士研究生，研究方向为卫星导航接收机基带处理算法。

国防科工局航天民用专项；北京市重点学科基金资助项目(No.XK100060525)

2014-05-22 收修改稿日期：2014-06-30

张晓林 1951年生，博士，教授，博士生导师，研究方向为信息与通信工程、集成电路设计、飞行器遥测遥控、航空航天电子系统、卫星导航系统。

郭九源 1992年生，在读博士研究生，研究方向为卫星导航、深空探测。