TDDM 信号的非对等广义差分捕获算法

李少玮， 孙 迅， 张荣兵

(北京遥测技术研究所 北京 100076)

TDDM 信号的非对等广义差分捕获算法

李少玮， 孙 迅， 张荣兵

(北京遥测技术研究所 北京 100076)

时分数据调制(TDDM)信号已经得到广泛使用，但现有的TDDM信号高灵敏度捕获算法主要依靠非相干累加提升灵敏度。为了实现弱信号环境下的TDDM信号捕获，提出一种非对等广义差分捕获算法。该算法对数据码和导频码的相关运算结果分别进行不同次数的广义差分相干累加，并将结果以非相干的方式合并，具有高灵敏度、高频域捕获分辨率的特点，适用于TDDM信号的高灵敏度捕获。通过建立MATLAB平台进行算法仿真，仿真结果表明该算法捕获灵敏度在数据长度为80ms时比常规算法高约1dB，数据长度为200ms时比常规算法高约1.5dB。

时分数据调制； 高灵敏度捕获； 非对等广义差分捕获

前 言

时分数据调制TDDM(Time Division Data Modulation)是新一代卫星导航系统中的一种信号调制方式，它以时分的方式交替发送有数据调制的数据码和无数据调制的导频码[1]，主要应用于GPS的L2C信号中，正在建设的北斗系统也可能采用这种数据调制方式。目前对TDDM信号的捕获算法研究较多，但均以捕获常规条件下TDDM信号的算法为主，对弱信号环境下(如室内、深空等)TDDM信号的捕获算法研究较少。因此，研究TDDM信号的高灵敏度捕获算法具有重要意义。

现有的TDDM信号高灵敏度捕获算法中，往往采取提高相干累加或非相干累加次数的方式。然而，相干累加受到导航数据翻转、残留多普勒频率等多个因素制约，累加长度受限；非相干累加存在“平方损失”[2]，累加增益较小。Shanmugam S.K.提出的广义差分相干累加[3]，增益高于非相干累加，同时具有频域搜索范围大、分辨率高的优点，更适用于高灵敏度累加。

本文首先介绍TDDM调制方式和合路捕获算法，分析比较非相干累加和广义差分相干累加的优缺点，然后利用TDDM信号中导频码无数据调制的特点，提出适用于TDDM信号高灵敏度捕获的非对等广义差分捕获算法，最后通过MATLAB建模并进行蒙特卡洛仿真，对非对等广义差分捕获算法的捕获性能进行验证。

1 TDDM信号及现有捕获算法

1.1 TDDM调制

TDDM调制以时分的方式将有数据调制的数据码和无数据调制的导频码调制为一个信号。TDDM信号的奇数位码片为数据码的码片，偶数位码片为导频码的码片，TDDM调制后码速率为数据码/导频码的两倍，TDDM调制如图1所示。

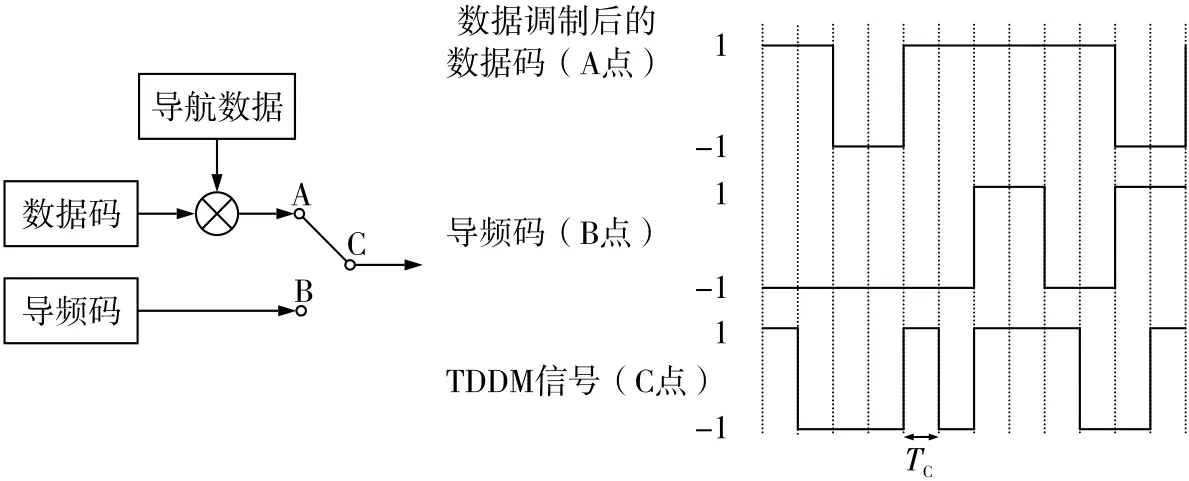
图1 TDDM调制示意图

图1中TC表示TDDM信号的码片宽度。

TDDM调制信号的表达式为：

其中，P为信号能量，sin(2πft+θ)为载波，cD(t)为数据码的码片，d(t)为卫星数据，cP(t)为导频码的码片。

由于导频信号无数据调制，因此可以通过增加相干累加长度得到更高增益，同时在跟踪时可以采用纯锁相环(PLL)进行载波跟踪。纯PLL增益比科斯塔斯环高6dB，虽然这种方法会造成3dB信号能量损耗，但仍将有3dB净增益[4]。

TDDM信号的性能相比常规信号有一定优势，但是其特殊的数据调制方式导致原有捕获算法不再适用。在不考虑相关运算内出现数据翻转的情况下，非TDDM信号的捕获相关峰不受导航数据影响，仅与码片延迟有关，但是用传统捕获算法捕获TDDM信号时，相关峰可能受到导航数据影响而消失。因此在捕获TDDM信号时需要消除导航数据的影响，或者将数据码和导频码分开捕获，这就对捕获算法提出了新的要求。

1.2 TDDM信号捕获算法

现有的TDDM信号捕获算法主要分为单独捕获导频或数据码[5～7]和同时捕获两路信号[8]两种方法。单独捕获数据或导频码将损失3dB信号能量，因此同时捕获两路信号的捕获算法更适合高灵敏度捕获。本文仅对同时捕获两路信号的捕获算法进行讨论。

合路捕获[8]是一种同时捕获两路信号并进行非相干累加的TDDM信号捕获算法。它产生两个本地伪码序列，分别与接收信号进行相关运算。两个本地伪码的数据码分别与“1”和“-1”相乘，导频码不变。接收信号经过下变频和降采样预处理后与两路本地信号分别进行相关运算，将两个相关运算结果非相干合并、累加后判决。合路捕获的结构如图2所示。

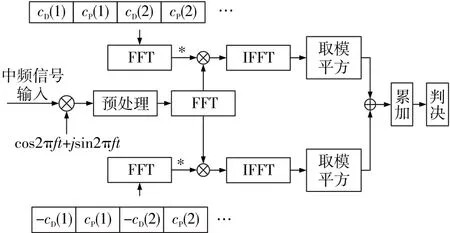
图2 合路捕获结构图

图2中，cD(i)表示本地产生的数据码，cP(i)表示本地产生的导频码，i＝1，2，3…L/2，L为相关运算长度，cos2πft+j sin2πft表示本地载波。

两个相关运算结果非相干合并后的结果可以表示为：

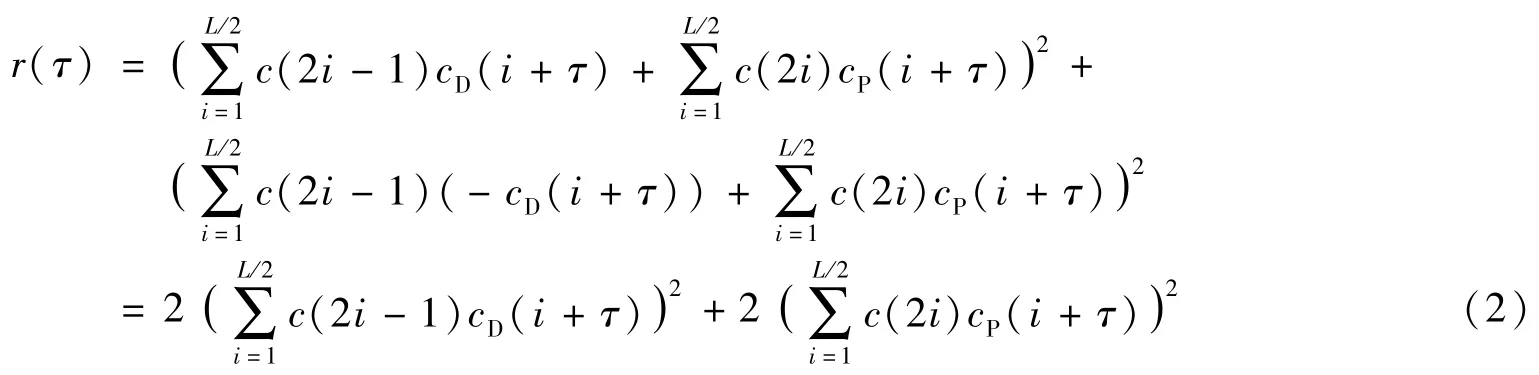
其中，c(j)表示接收信号的伪码，j＝1，2，…L，τ为码片延迟个数。由式(2)可以看出，合路捕获等效为将导频码和数据码分别进行相关运算后再非相干合并，消除了导航数据的影响，适用于TDDM信号的捕获。但由于合路捕获采取非相干的方式合并，因此累加方法只能采用非相干累加，致使灵敏度受限。

2 非相干累加与广义差分相干累加

2.1 非相干累加

非相干累加是一种常用的累加方法，它可以缓解残留多普勒频率导致的衰减，并消除非TDDM信号的导航数据。当不考虑噪声时，接收信号c(t)与本地信号c′(t)的相关运算结果为[2]：

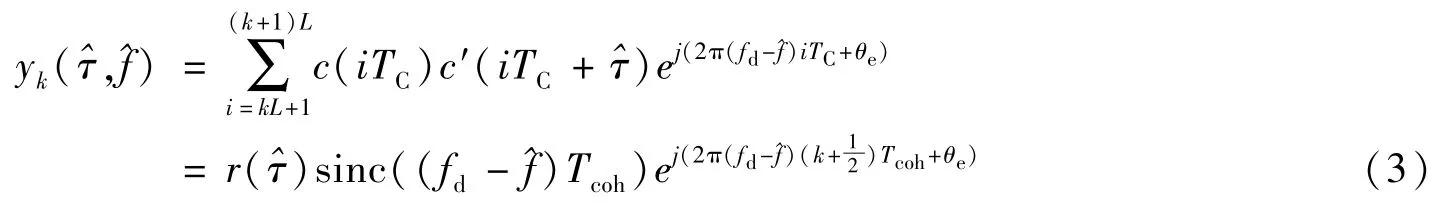
由式(3)可以看出，相关运算时接收信号载波与本地载波的频率差会引入值为sinc的损耗，这会减小捕获结果中的信号能量，从而降低捕获灵敏度。为了限制频差带来的损耗，搜索间隔一般为2/(3Tcoh)，当相关时间Tcoh＝10ms时，搜索间隔为66Hz。

经过NR次非相干累加后的检测值为：

由式(4)可以看出，非相干累加消除了载波相位信息，增加非相干累加次数不会加剧载波频差导致的损耗。

但是非相干累加也存在不足，在非相干累加时，噪声自身进行了平方运算，增加了噪声能量，降低了信噪比，这些信噪比损失通常被称为“平方损失”。要想弥补这些损失就需要增加非相干累加的次数，增加信号长度。

2.2 广义差分相干累加

广义差分相干累加通过累加不同延迟的差分相干累加结果达到提高捕获灵敏度的效果。在满足NRTcoh＞MTcoh，即NR＞M的条件下，最大延迟为M时广义差分相干累加的表达式为[3，9]：

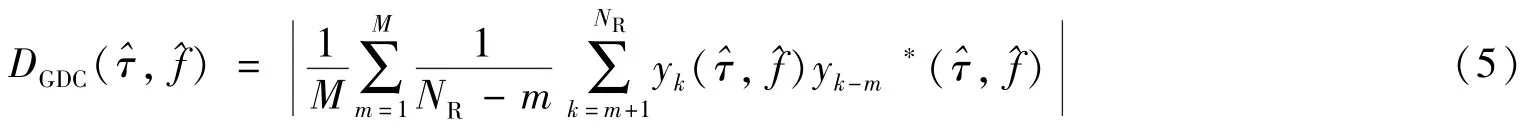
改变加法顺序，同时定义y0和y-1等负数项的值为0，式(5)可以近似写为：

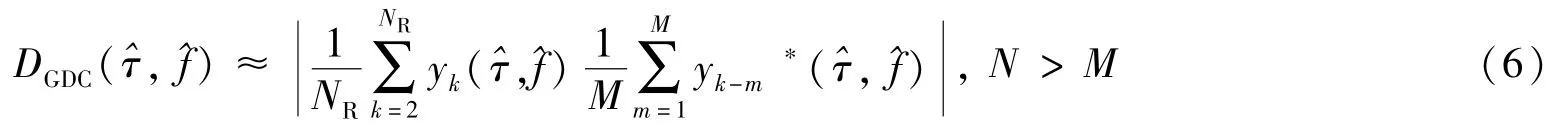
式(6)中将NR-m近似为NR，由于在高灵敏度捕获中往往有NR≫M，因此这种近似是合理的。从式(6)中可以看出，广义差分相干累加可以等效为将一段相关运算的结果与之前M段的结果之和进行差分相干运算，相关运算时间等效为MTcoh。因此，增加M的取值可以增加等效相干时间，提高捕获灵敏度，但同时也意味着更陡峭的载波频差损耗，更严重的数据翻转衰减。在只考虑多普勒频差的情况下，广义差分相干累加的检测值为：

从式(7)可以看出，残留多普勒频率对广义差分相干累加增益的限制与MTcoh有关，MTcoh越大，多普勒衰减越剧烈。FFT可以作为一种累加方式代替M次累加运算，并且在累加的同时进行频域捕获。

这种基于FFT的广义差分相干累加结构如图3所示。

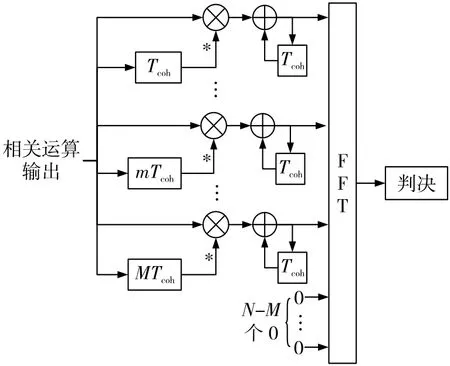
图3 基于FFT的广义差分相干累加

这种频率估计方法的频带范围ΓBW和分辨率ΓRES分别为[3]：

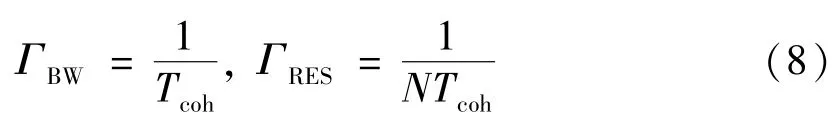
例如，当相关时间长度为1ms、FFT点数为16时，FFT捕获带宽为±500Hz，分辨率为62.5Hz。虽然当残留多普勒频率在FFT的捕获范围之外时，FFT结果会产生周期性模糊，但是可以通过扫频拼接FFT捕获范围的方法去除模糊度。可见，这种基于FFT的广义差分相干累加可以稳健地实现高灵敏度捕获和高分辨率频域捕获。

3 非对等广义差分捕获算法

为了充分利用导频码无数据调制的特点，本文提出了适用于TDDM信号的非对等广义差分捕获算法。该算法对导频码和数据码分别进行相关运算和广义差分相干累加，将两个伪码的捕获结果用非相干的方法合并后判决。其中导频码的累加次数为α，数据码的累加次数为β，α≥β并且α可变。

本文算法将下变频后的信号降采样至伪码速率2.046Mb/s。由于降采样时存在码相位的模糊度，直接降采样至伪码速率可能出现降采样累加起点位置在接收信号码片中间的情况，造成信噪比损失，因此本文将产生两组降采样数据来降低这种跨码片累加导致的损失。两组数据的降采样起点相差半个码片，其中一组的降采样起点与接收信号码片起始位置相差不超过半个码片。对两组数据分别进行捕获，在捕获相关峰中选最大值作为捕获结果，这种降采样方法等效于半码片步进。

降采样后的数据按照奇偶位分离为奇位数据和偶位数据。对于降采样起始位置与码片起始位置相差小于半个码片的一组数据，降采样后一个数据可以表示一个接收信号码片，因此奇偶数据的分离也意味着奇偶码片的分离。图4为其中一组降采样数据的奇偶数据分离示意图。

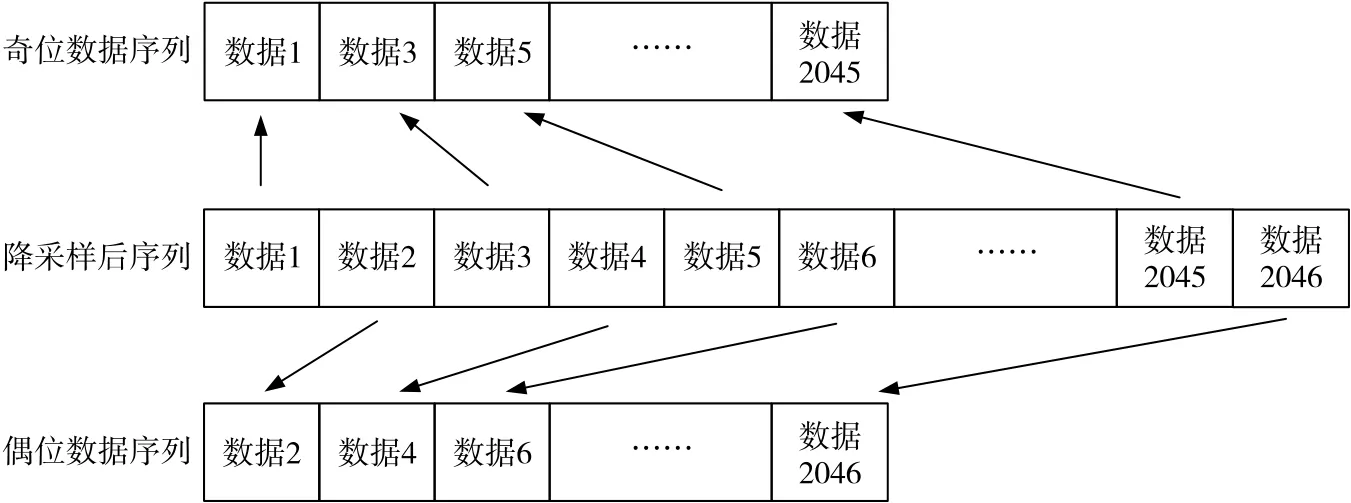
图4 奇偶码片分离示意图

由于信号的伪码相位未知，因此仅能确定奇位码片和偶位码片分别与导频码和数据码之一相对应。为了确定四者之间具体的对应关系，奇位码片和偶位码片都要与导频码和数据码进行相关运算。非对等广义差分捕获结构如图5所示。

图5 非对等广义差分捕获结构

由于接收信号的数据码码片在导频码码片之前，当接收到的偶位码片为数据码时，奇位码片为导频码，而前者的捕获相关峰位置比后者提前一个码片相位，因此与偶位码片进行相关运算的数据码需延后一个码片相位。

对于数据码，增大累加次数β会在提高灵敏度的同时增加数据翻转对捕获结果的损耗，当β≥20时会出现数据翻转导致的频谱分裂。图6所示为无噪声时，不同β值下非对等广义差分捕获算法的频域捕获结果。相关时间为1ms，数据长度100ms，α＝20。为了使曲线更光滑，FFT点数N＝1000。

图6 不同β值下非对等广义差分捕获算法的频域捕获结果(无噪声)

从图6中可以清晰地看出，当β＝10时，频谱正常；当β＝16时，频域捕获曲线出现明显分裂，频谱主瓣中心出现塌陷；当β＝20时，频谱中心塌陷严重，频谱分裂为两个主瓣。这种数据翻转导致的频谱分裂限制了β的取值。

对于无数据调制的导频码，增大α值不会导致频谱分裂，同时残留多普勒频率可以通过FFT进行捕获，因此在满足α＜NR的条件下增加α值不会带来损失。虽然差分运算的延迟越大，相关运算结果之间的相关性越差，导致α增加到一定的程度将不再提高捕获灵敏度，但是较高的α值仍然会带来高灵敏度和频域高分辨率的优势。

非对等广义差分捕获的相关运算长度Tcoh＝1ms，累加次数α＝20，β＝10，为了获得较宽的FFT捕获范围和较高的频域分辨率，同时考虑到FFT运算的效率，取FFT点数N＝32。根据式(8)，本算法的FFT频域捕获的有效捕获范围为1000Hz，分辨率为31.25Hz。

非对等广义差分捕获采用扫频法和FFT结合的方式进行频域捕获。扫频法将多个FFT的带宽拼接在频域搜索范围内，搜索间隔为660Hz。与常用于高灵敏度捕获的相关时间长度为10ms的合路捕获相比，本算法搜索次数降低到十分之一，频域分辨率提高了一倍，大大减少了相关运算次数，提高了捕获速度。

4 仿真验证与分析

为了验证非对等广义差分捕获算法的可行性，本文使用MATLAB搭建平台进行蒙特卡洛仿真，并与采用非相干累加的合路捕获算法进行比较。仿真采用TDDM+BPSK(2)信号，采样率为12.276MHz，中频频率为3MHz，伪码速率为2.046MHz，无载波多普勒频率，数据码和导频码采用长度为1023的不同C/A码，数据速率为50b/s。非对等广义差分捕获的相关运算时间为1ms，导频码累加次数α＝20，数据码累加次数β＝10，FFT点数N＝32；合路捕获的相关时间长度为10ms。仿真噪声系数为2dB。

仿真采用最大值检测，即设定一个门限，将超过门限的最大峰值判定为信号。最大峰值的位置即为捕获结果，当捕获结果与接收信号相同时捕获成功。

本文首先在载噪比为19～26dB-Hz的区间内每隔0.5dB-Hz进行200次蒙特卡洛仿真，每次仿真生成80ms信号，分别采用两种算法对信号进行捕获，并对捕获概率进行统计。统计结果如图7所示。

从图7中可以看出，信号长度为80ms时，非对等广义差分捕获的捕获概率明显高于合路捕获。如果以90%捕获概率为标准，非对等广义差分捕获可以捕获到载噪比约24dB-Hz的信号，与合路捕获比较优势达到1dB左右。

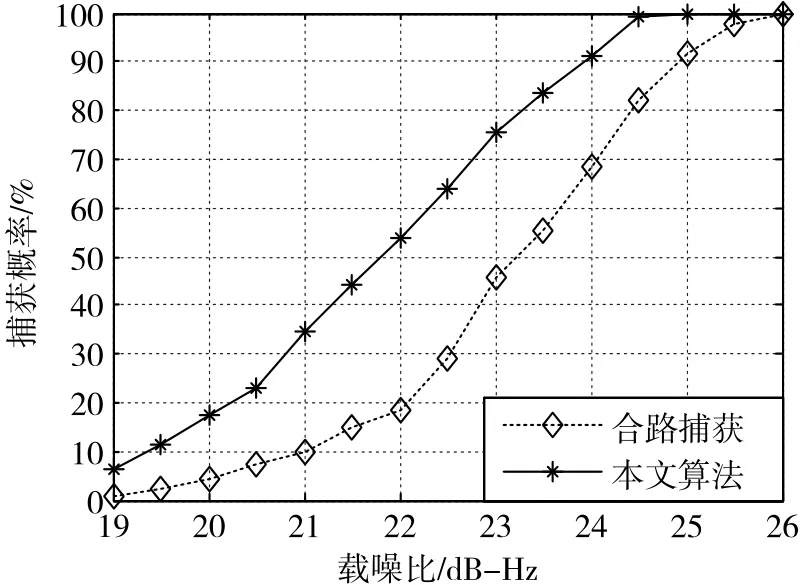
图7 不同载噪比条件下80ms数据捕获概率

其次在载噪比为17～24dB-Hz的区间内每隔0.5dB-Hz进行200次蒙特卡洛仿真，每次仿真生成200ms信号，分别采用两种算法对信号进行捕获，并对捕获概率进行统计。统计结果如图8所示。

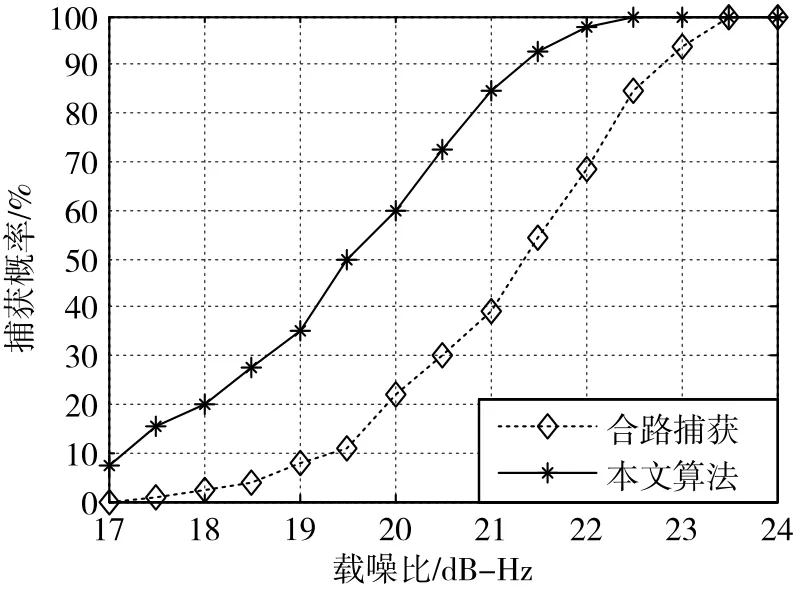
图8 不同载噪比条件下200ms数据捕获概率

从图8中可以看出，对200ms数据进行捕获时，非对等广义差分捕获可以捕获到载噪比低于21.5dB -Hz的信号，与合路捕获比较优势达到1.5dB左右。

对图7和图8进行比较还可以发现，将信号长度由80ms提高到200ms后，合路捕获灵敏度提高约2dB，非对等广义差分捕获的灵敏度提高约2.5dB，高于合路捕获。可以预见，增加信号长度可以使非对等广义差分捕获拥有更大优势。

5 结束语

本文介绍了TDDM信号的调制方式，比较了高灵敏度捕获常用的累加算法，针对TDDM信号的导频码无数据调制的特点提出了非对等广义差分捕获算法。该算法适用于TDDM信号的高灵敏度捕获，同时还可以实现高分辨率频域捕获，为跟踪环节提供更精确的多普勒频率估计值，频域分辨率提高2倍以上，频域搜索次数缩小10倍以上，大大减少了相关运算次数，提高了捕获速度。仿真结果表明，非对等广义差分捕获可以实现TDDM信号的高灵敏度捕获，其捕获灵敏度明显优于合路捕获，且增加累加长度获得的增益高于合路捕获。

[1] 谢 钢.全球导航卫星系统原理[M].北京：电子工业出版社，2013.

[2] 谢 钢.GPS原理与接收机设计[M].北京：电子工业出版社，2009.

[3] Shanmugam S K，et al.Enhanced Differential Detection Scheme for Weak GPS Signal Acquisition[C].ION GNSS 2007，USA：FortWorth，TX，2007，Sep.，26～29.

[4] Kaplan Elliott D，Hegarty Christopher J主编，寇艳红译.GPS原理与应用(第二版)[M].北京：电子工业出版社，2007.

[5] Moghaddam Ahmad R A et al.Exploiting the Orthogonality of L2CCode Delays for a Fast Acquisition[C].ION GNSS 19th International Technical Meeting of the Satellite Division，FortWorth，TX，2006，Sep，26～29.

[6] 胡晓峰，等.基于相位折叠的串行GPSL2C快速捕获算法[J].计算机仿真，2013，30(10)：95～98.

[7] 孙 亮.GPSL2C信号的捕获跟踪算法及软件实现[D].清华大学，2010.

[8] 刘 芳.新一代卫星导航信号的同步新机理研究[D].南京理工大学，2009.

[9] 韩 帅.GNSS系统弱信号捕获方法研究与应用[D].哈尔滨工业大学，2011.

Asymmetric Generalized Differential Coherent Acquisitio of TDDM Signals

Li Shaowei， Sun Xun， Zhang Rongbing

The Time Division Data Modulation has been widely applied in the Global Navigation Satellite System，but themajor high sensitivity acquisition algorithms of TDDM signals use noncoherent integration to improve the sensitivity.In order to acquire weak TDDM signals，an Asymmetric Generalized Differential Coherent Acquisition(AGDCA)algorithm is proposed in this paper. In the proposed algorithm，the correlation results of data code and pilot code are integrated different timeswith the genera differential coherent integration and combined with the noncoherent integration.The proposed algorithm has high sensitivity and high accuracy in frequency acquisition.The simulation resultswith MATLAB reveal that the proposed algorithm has1dB higher sensitivity than the conventional algorithm with data of 80ms，and 1.5dB higher sensitivity than the conventional algorithm with data of 200ms.

TDDM； High sensitivity acquisition； Asymmetric Generalized Differential Coherent Acquisition(AGDCA)

TP391.9

A

CN11-1780(2014)05-0036-06

李少玮 1989年生，硕士，主要研究方向为卫星导航技术。

2014-04-18 收修改稿日期：2014-05-19

孙 迅 1974年生，研究员，主要研究方向为卫星导航技术及抗干扰技术。

张荣兵 1980年生，高级工程师，主要研究方向为卫星导航信号处理及导航芯片设计。