解一道竞赛题的“通性通法”

●

(衢州高级中学何数思维工作室 浙江衢州 324006)

解题教学，我们教的不是解题技巧，而应该是解题的通性通法(“通性”是概念所反映的数学基本性质，“通法”是概念所蕴含的思想方法)．培养学生解题的通性通法，有利于培养学生普遍联系的观点和辩证思维的能力．

2014年浙江省高中数学竞赛于4月13日结束，在研究最后一题解题方法的过程中，笔者发现标准答案给出的是竞赛题的解题思路，方法自然，但因技巧性强，对培养学生的思维能力不是很好．就题目本身而言，肯定是培养学生思维能力的一道好题．那么，在解题教学中，我们应该怎样发挥它应有的作用呢？从基本概念、基本原理及其联系性出发，寻找题目所蕴含的数学方法，即所谓解题的“通性通法”，这才是根本．“通性”是概念所反映的数学基本性质，本题可以转化为解三角形问题，而解三角形问题的通性是正弦定理、余弦定理的应用；也可以应用求解几何问题的通性，就是转化为代数问题求解；还可以应用解方程组的通性，降次、消元、整体代换等．“通法”是概念所蕴含的思想方法，解三角形问题的通法是利用正弦定理或余弦定理进行边角互化；也可以考虑把代数问题转化为几何问题，应用坐标法求解；还可以应用消元法，方法自然，解法简洁，通俗易懂．

例1设正实数a,b,c满足

求a,b,c的值．

解法1(构造法)如图1，以O为出发点，作长度为a,b,c的3条线段OA,OB,OC,使得

∠AOB=90°，∠AOC=120°,

则

∠COB=150°.

由余弦定理知

于是

∠CAB=90°.

在Rt△ABO中，由正弦定理知

从而

在△ACO中，由正弦定理知

从而

因为

∠ABO=∠CAO,

所以

代入a2+c2+ac=4和a2+b2=3，求得

评注应用正弦定理和余弦定理求解三角形，是解三角形问题的通法．

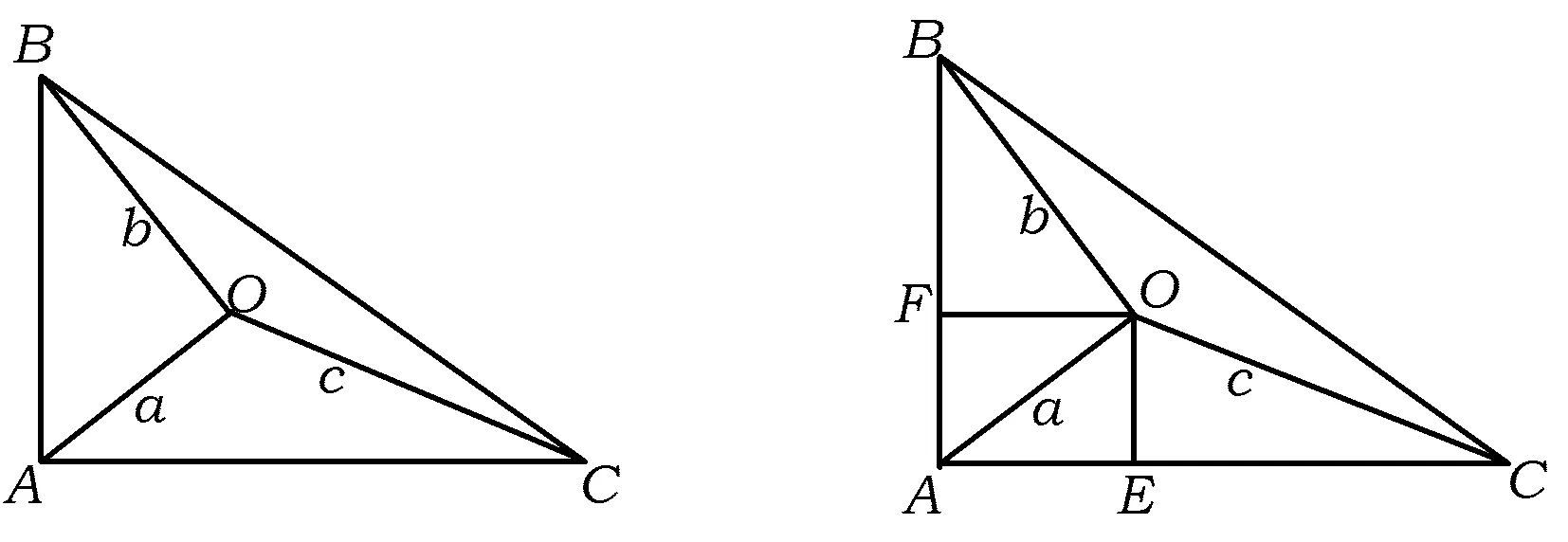
图1 图2

解法2(坐标法)如图2，以O为出发点，作长度分别为a,b,c的3条线段OA,OB,OC,使得

∠AOB=90°,∠AOC=120°，

则

∠COB=150°.

由余弦定理知

于是

∠CAB=90°.

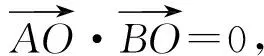
(1)

又直线AO和CO的夹角是120°，利用(到角)公式

得

(2)

联立方程(1)和(2)，求得

利用两点间的距离公式，求得

评注坐标法是以坐标系为桥梁，把几何问题转化成代数问题，通过代数运算研究几何图形性质的方法．它是解析几何中最基本的研究方法之一．其实，许多几何问题都可以应用坐标法．本题应用坐标法，把复杂的运算问题简单化．另外，本题也可以利用夹角公式求解．

解法3(消元法)因为3+4=7，所以

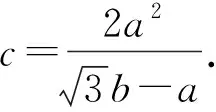
(3)

由a2+c2+ac=4,得

4-a2=c(a+c),

(4)

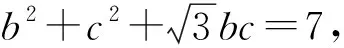
(5)

式(4)除以式(5),得

(6)

联立方程(3)和(6)，消去c，得

因为a2+b2=3，所以

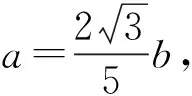
评注利用常规的求解三元二次方程组的消元法，结合降次、整体代换等解题的通性通法完成解题．另外，从该解题方法我们可以看出，题目的已知条件“正实数a,b,c”可以推广到“实数a,b,c”(答案作相应的调整，此处略)．

在解题教学中，注重基本概念、基本原理及其联系性，把握解题的通性通法，不仅是培养学生思维能力的根本，而且也是发展学生思维能力的正道．

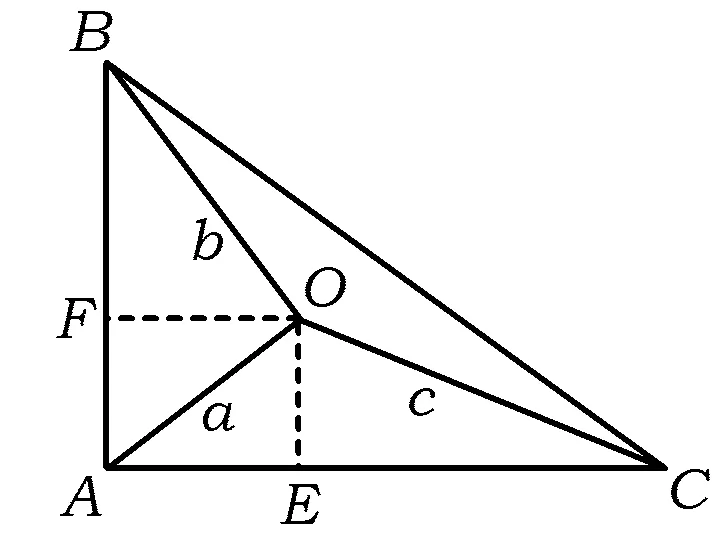
图3

另附标准答案：如图3，以O为出发点，作长度为a,b,c的3条线段OA,OB,OC,使得

∠AOB=90°,∠AOC=120°,

则

∠COB=150°.

由余弦定理知

于是

∠CAB=90°.

过点O作OE⊥AC,OF⊥AB,设AE=m，OE=n,由∠ABO=∠OAE,得

即

又∠AOC=120°,得

即

于是

从而

参 考 文 献

[1] 章建跃．什么是好数学教学[J]．中小学数学(高中版)，2011(7/8)：封底．

[2] 章建跃．注重通性通法才是好数学教学[J]．中小学数学(高中版)，2011(11)：封底．

[3] 章建跃．注重课堂生成才是好数学教学[J]．中小学数学(高中版)，2011(12)：封底．