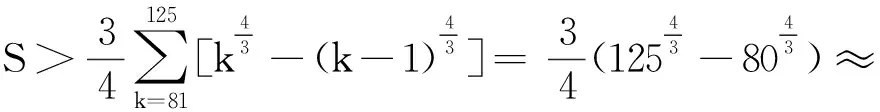基本功显内力 创造力解新题
——例析导数背景下如何证明与正整数有关的不等式问题
2014-08-08
●
(黄陂一中盘龙校区 湖北武汉 430312)
在导数问题背景下证明含有正整数的不等式问题,一般都设置有几个小题,最后证明不等式.这类问题一般可以用数学归纳法或者不等式适当放缩进行证明.命题者通常还有一个重要意图是利用前几个小题中已经得出的结论,充分发挥学生的创造力,把函数中的变量x用含有n的式子进行替换,再通过适当变形证明不等式.但是如何替换及变形对学生来说是难点,应该怎样突破呢?下面归类分析,帮助学生解决这个问题.
1 证明含有二元正整数的不等式

(1)求实数a的值;

分析(1)a=1.
(2)g(x)的单调增区间为(0,1),(1,+∞).

亦即
得
因为m>n>1,由第(2)小题可知g(x)在(1,+∞)上单调递增,所以
g(m)>g(n),
即
点评含2个变元的不等式,通过变形(2边取对数、取倒数等),把它变形为一个函数f(x)背景下2个函数值的大小f(m)≥f(n)(或f(m)≤f(n))形式,再根据函数的单调性得出结论.
2 证明含有一元正整数的不等式
2.1 直接替换,再求和

(1)当a=2时,试比较f(x)与1的大小;
分析(1)当a=2时,
①当x>1时,f(x)>1;
②当0 ③当x=1时,f(x)=1. (2)根据第(1)小题的结论,当x>1时, 即 从而 又 于是 点评含有一元正整数不等式的证明,且是求和形式,可联想 分析(1)实数k的取值范围为(-∞,2]. (2)由第(1)小题,当x≥1时, 即 从而 将以上不等式2边分别相加,得 但与所证结果有“距离”,再从右边观察推理,需将替换后的式子进行一次放缩,即 再2边求和,不等式得证. 例4已知函数f(x)=ex-ax-1(其中a>0,e为自然对数的底数). (1)求函数f(x)的最小值; (2)若f(x)≥0对任意的x∈R恒成立,求实数a的值; (3)在第(2)小题的条件下,证明: 分析(1)f(x)的最小值为 f(lna)=elna-alna-1=a-lna-1. (2)f(x)≥0对任意的x∈R恒成立,即在x∈R上,f(x)min≥0,易得a=1. (3)由第(2)小题知,因为a=1,所以对任意实数x均有 ex-x-1≥0, 即 1+x≤ex. 得 e-(n-1)+e-(n-2)+e-(n-3)+…+e-2+e-1, e-(n-1)+e-(n-2)+e-(n-3)+…+e-2+e-1+1= 此时“顺序颠倒”着出现结果,不等式得证. (1)用a表示b,c; (2)若f(x)≥lnx在[1,+∞)上恒成立,求实数a的取值范围; (2010年湖北省数学高考理科压轴题) 解得 其中x≥1,当x=1时取到等号.当x>1时, 即 依次令k=1,2,3,…,n,得 … 各式相加得 原不等式得证. 2边求和得到不等式 例6已知函数g(x)=x2-(2a+1)x+alnx. (1)当a=1时,求函数g(x)的单调递增区间; (2)若函数g(x)在区间[1,e]上单调递增,求a的取值范围; (3)在第(1)小题的条件下,设f(x)=g(x)+4x-x2-2lnx,证明: (参考数据:ln2≈0.693 1.) (2)函数g(x)在区间[1,e]上单调递增,则a≤1. 由x∈[2,+∞),h′(x)<0,得 即 又 k-f(k)=lnk, 此时右边如何得到是难点.从要证明的结果分析,要“善”变形,如 也即 “巧”构造函数 例7设n是正整数,r是正有理数. (1)求函数 f(x)=(1+x)r+1-(r+1)x-1 (其中x>-1)的最小值; (2)证明: (2013年湖北省数学高考理科压轴题) 分析(1)f′(x)= (r+1)(1+x)r-(r+1)= (r+1)[(1+x)r-1], 从而f(x)在(-1,0)上单调递减,在(0,+∞)上单调递增,得 f(x)min=f(0)=0. (2)由第(1)小题知:当x>-1时, (1+x)r+1>(r+1)x+1(伯努利不等式), 所证不等式即为 若n≥2,则 nr+1-(r+1)nr<(n-1)r+1, 从而 (1) 因为 所以 故式(1)成立. 若n=1,则nr+1-(r+1)nr<(n-1)r+1显然成立.由 nr+1+(r+1)nr<(n+1)r+1, 得 (2) 因为 所以 故式(2)成立.原不等式成立. (3)由第(2)小题可知:当k∈N*时, 210.225, 210.9, 于是 [S]=211. 再用叠加法求和. 在导数背景下含正整数的证明问题,作为压轴题其解答方法虽然很多,但是在高考中能新颖别致、颇具创意地完整解答的学生很少,大部分学生会采用通性通法.压轴题的命题思路,往往是环环相扣,“递进”式设问,既能考查学生的功力,又能考查学生的灵性,让优秀的学生能脱颖而出.但是在高考有限时间内真正能做对做全的学生极少,学生常常在关键位置“迷路”.因此教师应加强对压轴题的研究,帮助学生逐步掌握解答压轴题的策略,学生也就不会望而生畏,更不会果断放弃.学生在平时的备考复习中要增强信心,多思考、多积累,从而提高压轴题的得分率.
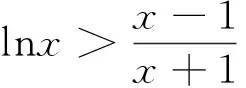
2.2 替换,放缩,再求和
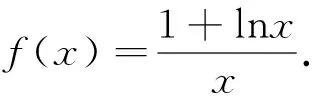
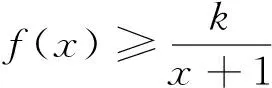
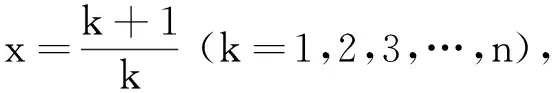


2.3 “巧”替换,“活”变形,再求和
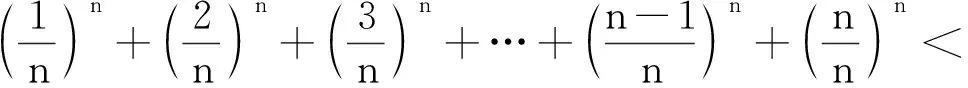
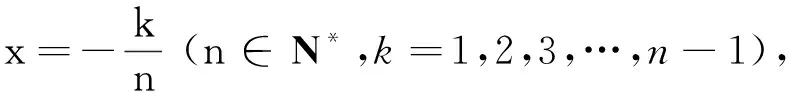



2.4 替换,变形,添(减)项
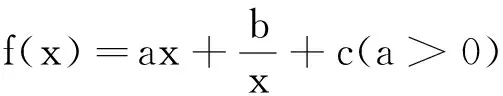

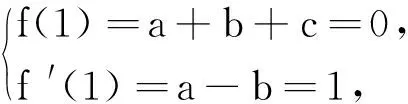


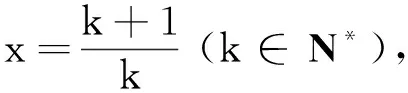
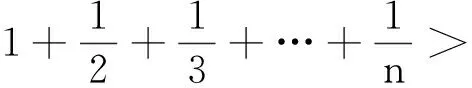

2.5 执果索因,恰当替换,“活”变形,“巧”构造

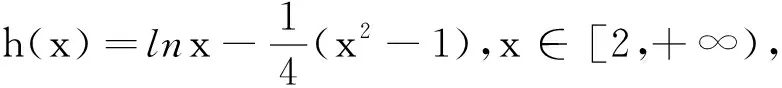
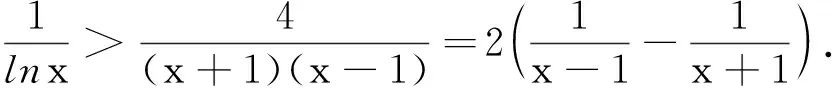

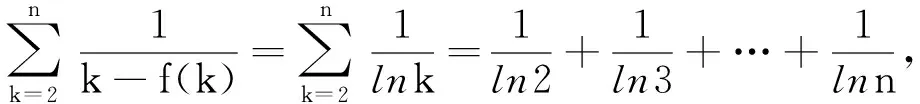
2.6 “灵活”变形,“恰当”赋值,“叠加”求和