让解法来得更自然一些
2014-08-08
●
(芷兰实验学校初中部 湖南常德 415000)
每年的中考题不乏优秀的智慧题,但由于这类题型要么是填空题,要么是选择题,即使是解答题,也往往只要求直接写出结果,使得研究它们解法的观点高、解法巧,甚至长篇大论的文章层出不穷.这既不是命题者最初的动机,也不是学生能轻易吸收、经常使用的.笔者认为让解法更自然一些,会更适合学生模仿、跟进与创新!
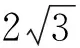
原解法文献[1]中先引进参数,后消参,最后用平面上两点间距离公式求解,大多是高中的知识和方法,更有大量的逻辑演绎推理,不适合学生阅读.
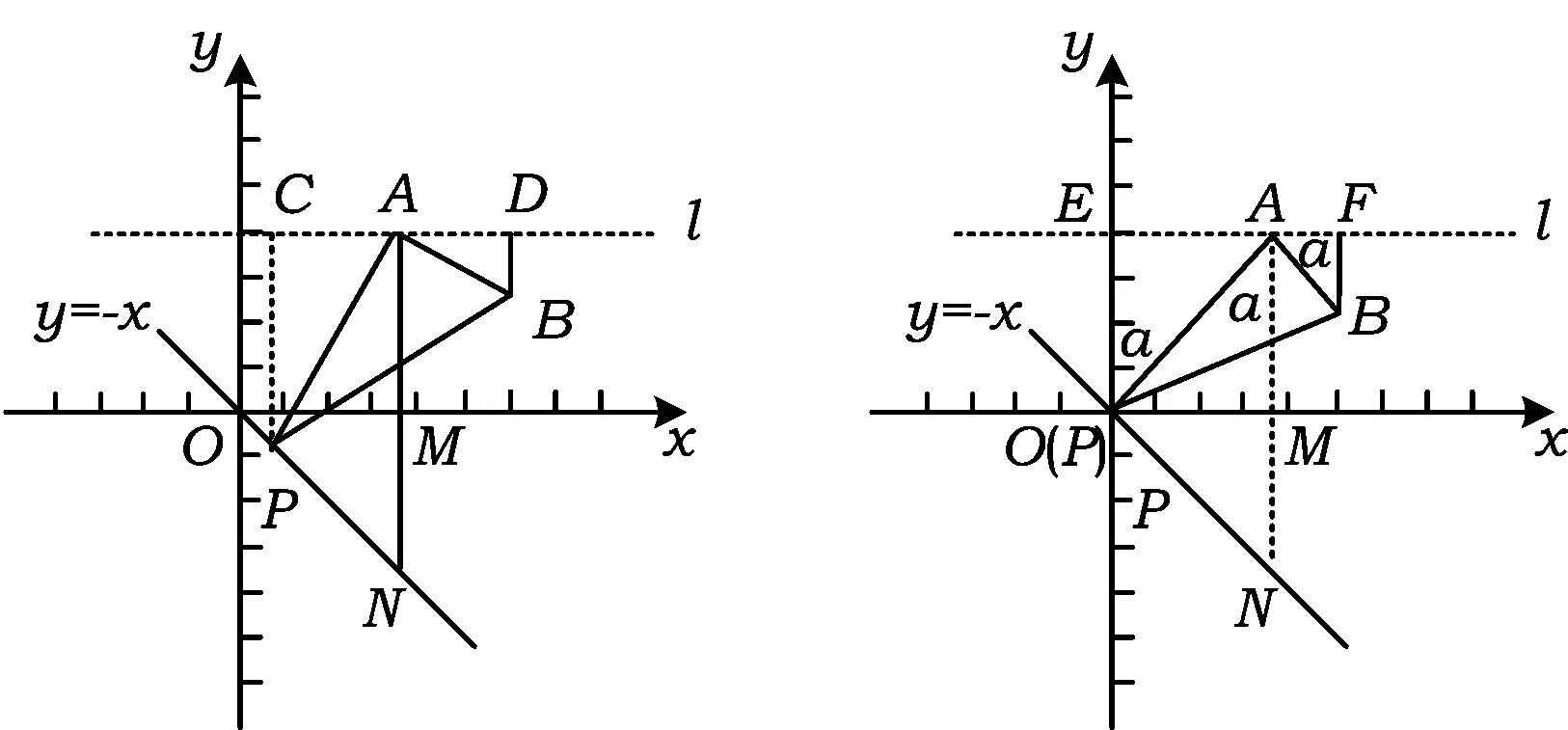
图1 图2
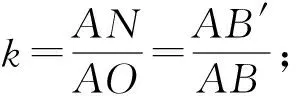
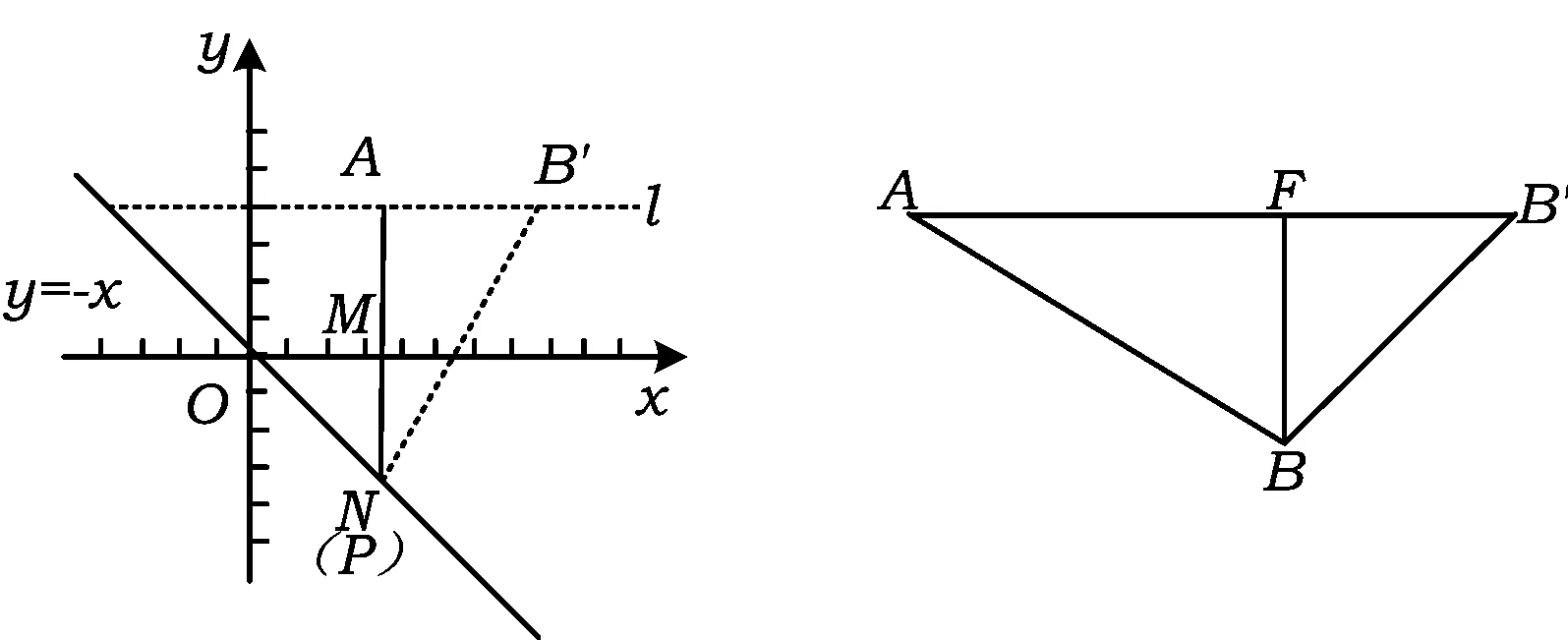
图3 图4
令∠EOA=∠OAM=∠BAF=α,由旋转知AO,AB绕点A逆时针旋转α得到AN,AB′,此时OA,AB放大k倍得到AN,AB′,从而
在Rt△AMO中
在Rt△ABO中
于是
此时为求BB′分离出图4,其中
于是
最后在Rt△BB′F中
即为点B的运动路径长.
例2如图5,在平面直角坐标系xOy中,已知正△ABC的边长为2,点A从点O开始沿x轴的正方向移动,点B在∠xOy平分线上移动,则点C到原点O的最大距离是______.
原解法文献[2]可谓引经据典,文献[3]给出了一个更“高级”的辅助圆法,可谓精彩纷呈,这又让人疑惑是说给老师听还是给学生看.

图5 图6
笔者分析几何问题常法:变中寻不变.正△ABC的边长AB在移动过程中不变,其面积也不变,于是由所求量“距离”联想到面积法.

显然此时
OC≥CM+ON.
当CM(高)=CP(斜边)时,正△ABC面积有最大值,此时ON(高)=OP(斜边),△OAB面积也有最大值,于是CO⊥AB且CO平分边AB,此时有OB=OA=x(如图6).
在Rt△ABF中,
BF2+FA2=AB2,
即
从而
又
即
得
于是点C到原点O的最大距离为
解题教学建议教解题方法、写解题文章,拓展也好,变式也罢,笔者认为教或写的着力点是引领,是把复杂的东西简单化,难理解的东西通俗化,而不仅仅是更高级的发挥:解题是给别人认可的,不是孤芳自赏的.作为教师,我们更应该少一些纸上谈兵、多一些实用性,因此笔者认为:让解法更自然,才更适合学生.
参 考 文 献
[1] 马先龙.探明路径后求其长[J].中学数学杂志(初中),2014(2):60-61.
[2] 朱玉祥.一道填空题的高零分率引发的思考[J].中学数学教学参考(中旬),2014(4):59-60.
[3] 仝会军.由质疑引发的思考[J].中学数学教学参考(中旬),2014(6):66-67.
