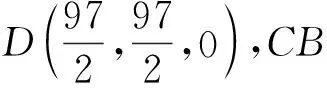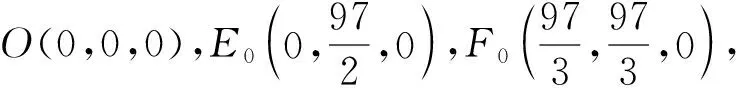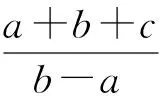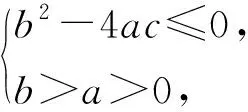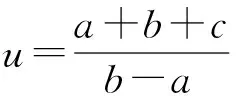巧用降维策略 破解数学难题
2014-08-08
●
(北仑中学 浙江宁波 315800)
1 从一道高考试题谈起
2014年浙江省数学高考结束后,绝大多数考生觉得试题太难了,有许多高中数学教师也认为它是浙江省近5年数学高考试题中最难的一套试题.事实上,其中的解答题没有特别难的地方,考生感到难的主要原因是有几道选择题和填空题不是很“厚道”,其中的第10题(选择题压轴题)成了许多考生的“滑铁卢”,有的考生花费了很多时间,但是答案还是“千呼万唤不出来”;有的考生经过漫长的推算,最后终于得到正确答案,但由于耗时过多,影响了后面试题的解答.文献[1]中介绍了对这一试题的2种解法,但这2种解法都要经过大量的推算才能得到结论,也是许多考生在考场上所采用的解法.笔者认为这2种解法都不是命题教师所希望看到的解法.
等价转化思想是中学数学中最重要的数学思想方法之一.许多所谓的数学难题,一般可以通过等价转化的方法,把它化归为相对简单的问题;其中数学难题之所以是难题的一个重要原因是参变量的个数太多,即“维数”太高所致;若能通过合法、有效的途径减少参变量的个数,把“三维”问题“二维”化,“二维”问题“一维”化,则往往能找到解题的通途.
对于这道选择题压轴题,事实上只要考察所涉及的函数图像在y轴上的投影,即把“二维”问题“一维”化,问题就很容易解决了.也许这才是命题教师所希望看到的解法!
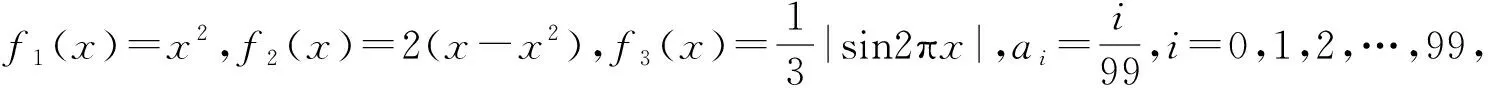
( )
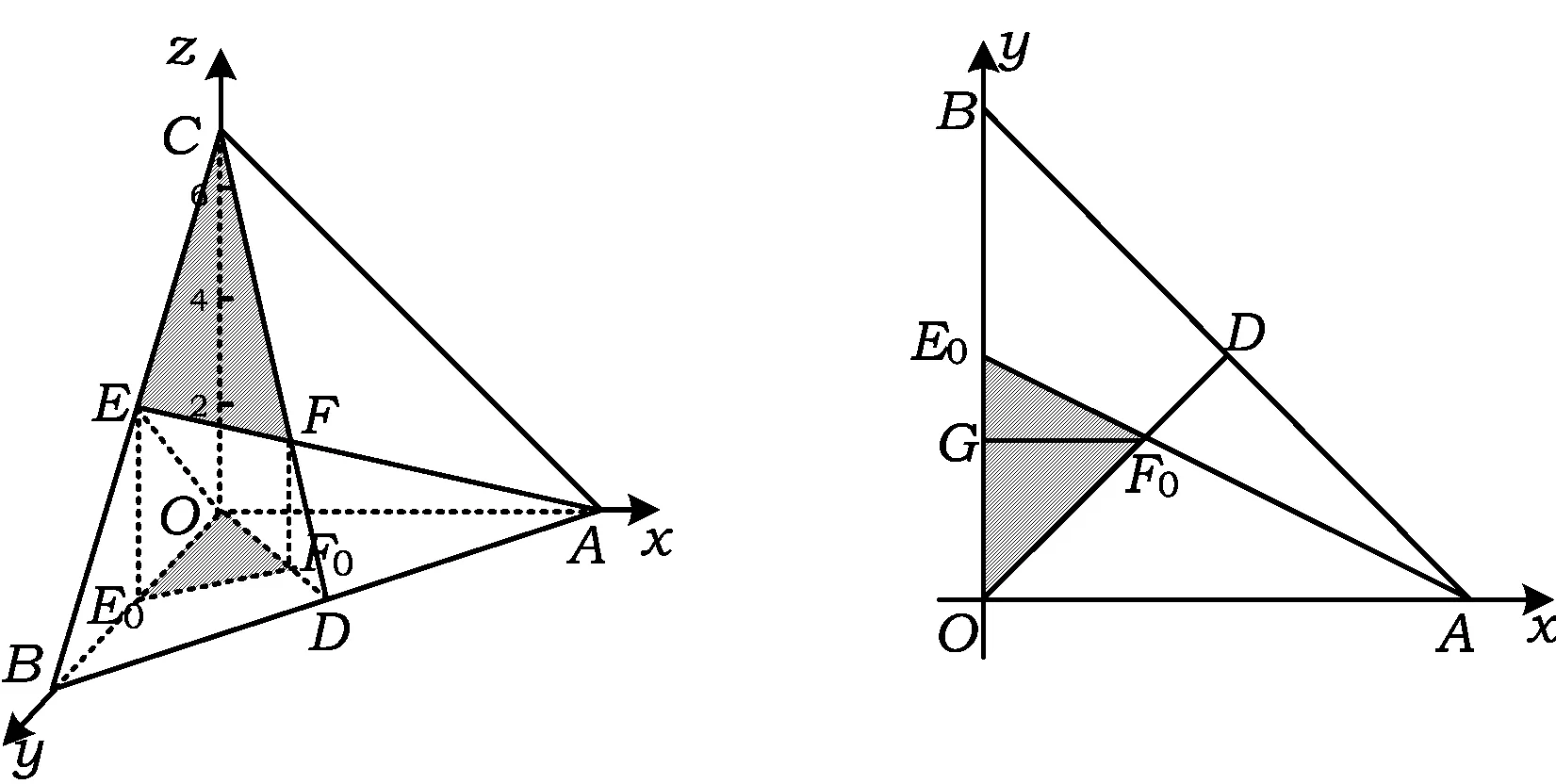
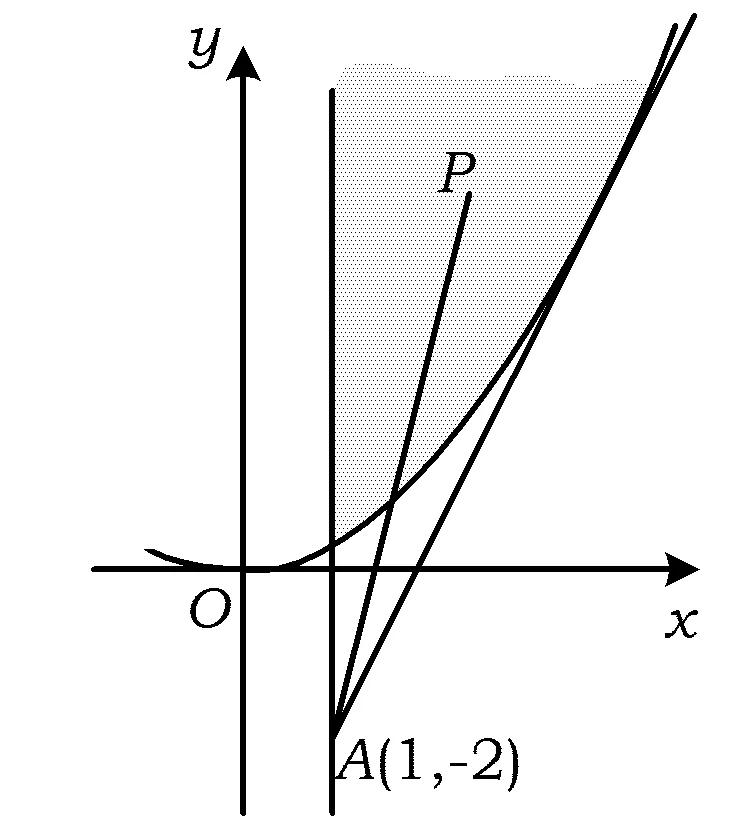
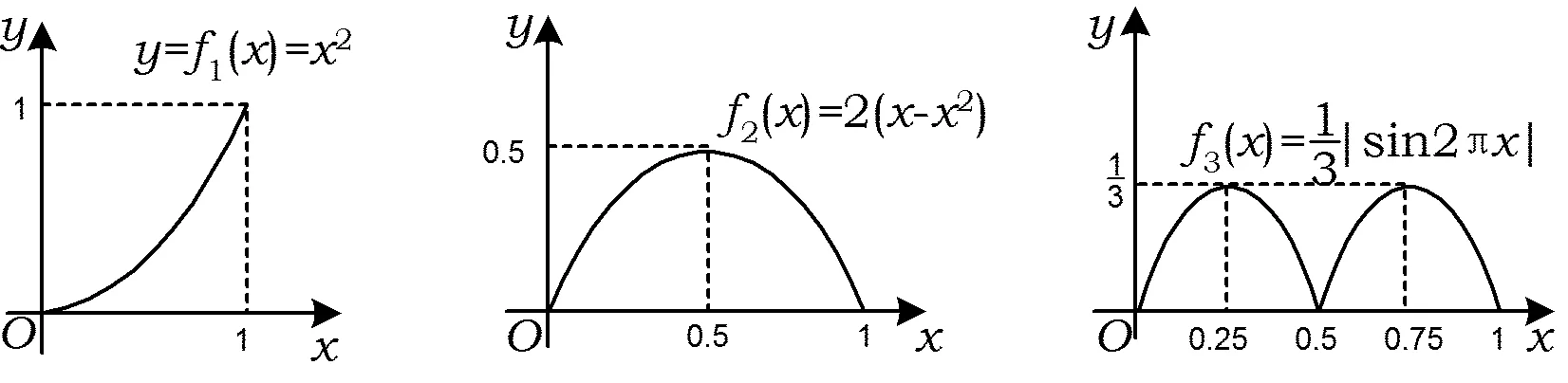
A.I1 C.I1 (2014年浙江省数学高考理科试题第10题) 图1 (1)由于f1(x)=x2是[0,1]上的增函数,因此I1=u1=1. 综上所述可得I2 例2以正100边形的顶点为顶点的两两不全等的三角形的个数为______. 解(第1次转化)正100边形的顶点将其外接圆分成100等份,设三角形的3个顶点之间的弧分别含x,y,z等份,则x+y+z=100,且原问题等价于不定方程x+y+z=100(x≤y≤z)的正整数解(x,y,z)的个数,也等价于不定方程x+y+z=97(x≤y≤z)的非负整数解(x,y,z)的个数. (第2次转化)如图2,在空间直角坐标系中,设A(97,0,0),B(0,97,0),C(0,0,97),则平面AB的方程为 x+y+z=97, 图2 图3 (计算答案)如图3,作F0G⊥OB于点G,则△OGF0内(包括边界)中整点的个数为 则△E0GF0内(包括边界)中整点的个数为 △OE0F0内部(包括边界)中整点的个数为561+272=833,因此不全等的三角形的个数为833个. 评注当问题化归为:“求不定方程x+y+z=100(其中x≤y≤z)的正整数解(x,y,z)的个数”以后,也可通过代数方法解决,但对运算能力的要求较高,且较难验证结论的正确性.本解法运用数形结合的思想,把问题化归为“求△CEF内部(包括边界)中整点的个数”(在三维空间中),再化归为“求△OE0F0内部(包括边界)中整点的个数”(在二维空间中),最终得到结论,思路自然、过程清晰、形象直观. 分析本题是一个关于a,b,c的三元函数最值问题,因此把条件化归为关于a,b,c的不等式组后,若能化为二元函数,甚至是一元函数的最值,问题就容易解决了. 图4 设过点A(1,-2)的曲线x2=4y的切线的斜率为k(k>0),则其方程为y=k(x-1)-2,代入x2=4y整理得 x2-4kx+4k+8=0. 由Δ=16k2-16(k+2)=0(其中k>0),得k=2,从而kAP的最小值为2,故umin=3. 看不清试题的本质所在是造成解题困难的重要原因之一.若能通过等价转化的方法,剥去问题的“过度包装”,显露其本质所在,再注意减少问题的参变量个数,即注意降维策略的使用,则往往能使问题“柳暗花明”. 参 考 文 献 [1] 徐丽华.2014年浙江省高考数学理科卷选择题压轴题解析[J].数学通讯,2014(7)(下半月):52-54.
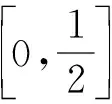
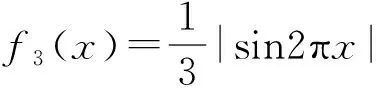
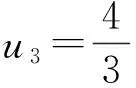
2 降维对策的应用举例