关于数学命题的一些想法

●

(稽山中学 浙江绍兴 312000)

命题能力是高中数学教师必须具备的专业素质之一，它是课堂教育、教学辅导、解题研究等能力所不能替代的重要的教师基本功之一，也是教学水平、教师素养、专业功底和教学研究能力的综合体现.从现阶段的高中数学教学实际情况分析，许多高中数学教师的命题能力是不够的，其中的重要原因是忽视了命题能力的重要意义，很少把命题作为教学研究、业务培训和专业发展的重要内容.在现有的教育教学研究书刊上也很少涉及有关命题的问题.本文通过命题实践的一些想法来说明命题过程实质上是研究数学本质、数学思想、数学知识、数学问题和解题方法之根本的过程.期望能引起高中数学教师对命题的重视.

命题主要包括命题设计和编制试卷，同时要考虑评价过程和效果分析.

1 命题的题型

1.1 从命题的作用和目的分

从命题的作用和目的分，一般有以下几种题型：

1.1.1 知识题

考查知识点的掌握程度.一般来说，这类题目直接来源于数学知识，比较直观和简单.

(2014年浙江省数学高考理科试题第12题)

1.1.2 知识应用题

考查理解、掌握知识的程度.这类题目要求应用的知识点比较明确，方法直接，技巧能力和运算能力要求不高.

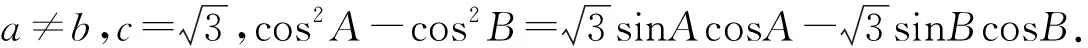
(1)求角C的大小；

(2014年浙江省数学高考理科试题第18题)

1.1.3 能力题

在知识点的基础上，考查数学基本思想、基本思维、基本方法、基本能力等数学学习和解决问题的能力，重在数学能力的体现，属于较高要求的题型.

(2014年重庆市数学高考理科试题第15题)

1.1.4 计算题

在数学知识的基础上，考查数学的重要能力——运算能力，包括数字运算、字母运算和数学式运算等.这类题目对数学其他能力要求一般，重在体现运算能力(包括方法、技巧和运算的逻辑性、严谨性).在每年的数学高考卷中一般都有出现.

图1

(1)已知直线l的斜率为k，用a,b表示点P的坐标；

(2)若过原点O的直线l1与l垂直，证明：点P到直线l1距离的最大值为a-b.

(2014年浙江省数学高考理科试题第21题)

1.1.5 讨论题

讨论题是体现数学思维能力较高要求的一类题.在数学知识的基础上考查数学思维、运算、演绎、逻辑推理能力,区分不同条件下分类讨论和解题书写表达的能力.

例5已知函数f(x)=x3+3|x-a|(其中a∈R).

(1)若f(x)在[-1,1]上的最大值和最小值分别记为M(a)，m(a),求M(a)-m(a)；

(2)设b∈R,[f(x)+b]2≤4对x∈[-1,1]恒成立，求3a+b的取值范围.

(2014年浙江省数学高考理科试题第22题)

1.1.6 探索题

在数学知识、能力的基础上考查一定的数学创新、探索、研究能力，属于较高要求的题型.此类题目在以往高考题中常有出现,由于在限定时间内探索研究的时间难以把握，近几年的高考中出现较少.

1.1.7 技巧题

考查数学解题的一些典型、特殊的方法和解题技巧，体现创造能力、数学潜力和数学才智.但新课标考纲中明确指出数学高考要求通性通法，因此专门考查技巧的题型在高考中已较少出现，一般都在能用通法解决的一些客观题上体现一下特殊的方法技巧.当然，在平时的教学和练习时，设计一些技巧题，还是很有必要的，这对于激发学生学习兴趣、体现数学灵活性、培养学生数学智慧是很有意义的，而且典型、特殊的方法技能对于快速、正确地解题，尤其是解决客观题，或者是检验通性通法的结论是很有益处的.

例7设实数x，y满足

求x+y的值.

1.1.8 应用题

根据新课标要求，数学应用题是作为一种应用能力来要求的，考查能否将实际问题转化为数学问题，建立数学模型，利用数学知识、数学思想进行分析并解决.在实际命题中，由于对应用题的背景信息的合理性、公平性很难把握，近几年的数学高考试题中应用题出现的也比较少.

1.2 从命题的形式分

从命题的形式分，一般有3种题型:

1.2.1 选择题

国内高中数学的选择题一般采用的是单选题，解答要求方法简捷、灵活，能快速、正确解答.与解答题的解法要求不同，选择题不需要写出详细的演绎、推理、运算过程，因此命题设计和解答方法更显灵活多样.

选择题的4个选项设计，除了正确答案，其他3个选项一般是来源于由于审题不清、忽视隐含条件、计算错误、增根或漏解等产生的错误，也称为设置“陷阱”，也是选择题的特点之一.在平时练习时，这种“陷阱”可以提醒学生养成认真、仔细、严谨的数学学习习惯，但在考试时容易使粗心的考生造成非知识能力因素的失分，尤其当“陷阱”设计在第1个选项时，考生更容易上当.近几年的高考一般避免故意设计“陷阱”的做法.如果其他3个选项回避了易错的情况，考生只要会做，即使失误，也可以自觉找出错误而正确解答.这对考查考生的数学知识和能力来说是有利而公平公正的.当然这样也就失去了这一设计选择题的特有方法.

对于演绎、推理、计算繁杂，书写困难或花费时间，解答过程评改判分难以把握的问题，也可以用选择题的形式呈现，有利于评改时的客观、公正，这也是选择题作为客观题的意义之一.

判断类型的问题，如图像形状、图形关系、大小关系、类比关系、命题判别等也需要用选择题的形式呈现.如2014年浙江省数学高考理科第2,4,7,8,9,10题，比较恰当的呈现方式就是选择题.

需要用一些特殊技巧方法解决而又难以表述时，也可以采用选择题.

选择题的特点是解法比解答题更多样灵活.除了通性通法，有些选择题能较好地体现考生数学方面的学习能力、数学智慧、数学自觉和数学潜能，或者说是数学“天赋”.

选择题的解法经常用到数形结合、合理猜想、类比判断、极端情况、特殊赋值、筛选排除等，正确的解法往往符合选择题的特点和命题意图，从而事半功倍.

经常可以看到，对于命题教师设计的有相当难度的选择题，有些聪明的考生用合理的“投机取巧”的方法能很快得到正确答案.他们的“方法”回避了命题设计的意图和考点，使难点并不存在，这或许是选择题的一种特色.

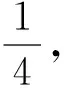
1.2.2 填空题

填空题与选择题一样属客观题，除了没有选择题的4个选项设计外，基本与选择题一样.但它避免了考生猜测答案的情况，比选择题更合理、公平和客观.因此现在有的省市高考已不再采用选择题，而全用填空题作为客观题，如2014年江苏省数学高考就采用了14个填空题.

但是填空题同样有一个考生规避命题意图难点的问题.比如，像变量情况下的定值问题，一定可以由特殊点得到该定值.

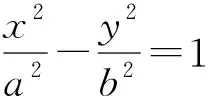
此题意图采用平面几何、三角形内切圆性质和双曲线焦点、定义相结合的解题方法，是一个设计很好的命题.但若考虑到点P无限接近于右顶点时，△F1PF2的内切圆心必然是右顶点，则内切圆心的横坐标必须是a，这样就规避了命题的考点.

(2014年浙江省数学高考理科试题第13题)

事实上，一般的线性规划问题，都可以用3条边线的交点代入解决.

由此可见，现有的选择题、填空题作为客观题，其客观性主要反映在评判的过程中.是否能客观体现出命题设计的考点和意图还需要在命题时深入思考.

1.2.3 解答题

相对于选择题、填空题来说，它要求呈现完整的解题方法、步骤，在书写过程中体现出数学思想、知识掌握、方法运用、演绎推理、运算求解的能力以及认真严谨的数学态度.因而，除了答案，其解题过程也是重要的考查要求和评价依据.在评改时，容易带有评改人的主观因素，也考验了评判的合理、准确、公平和公正性.这些都是解答题的特点.

2 命题的来源

命题要以数学基础知识、基本方法为依据，突出主干知识、重要内容、通性通法和数学思想、数学能力、创造性思维.

编制题目一般可以从以下几个方面设计相应的题型.

(1)从数学知识点出发，以概念、定义、公理、定理、公式、常识结论及应用为目标进行设计.

(2)从易忽视、易模糊、易产生错误的问题设计.

(3)以数学思想、常用解题方法为依据设计命题，考查数学思想方法的掌握和解决问题的能力.

(4)以数学基本能力和重要技能为基础设计命题,考查数学能力和重要技能的掌握及在解题中的应用，体现学习数学的能力和智慧.

(5)以教材中的例、习题和思考、探究性问题为核心延伸、拓展、改变设计命题.

(6)以各类知识间的类比设计命题,如数形之间，函数与数列之间，方程根、图像交点与函数零点之间，平面几何、解析几何、立体几何之间的类比等.

( )

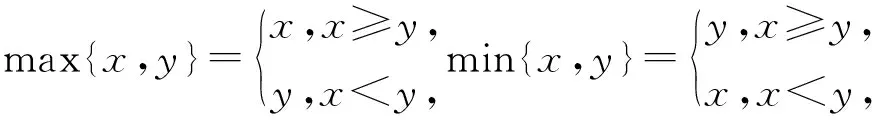
A.min{|a+b|,|a-b|}≤min{|a|,|b|}

B.min{|a+b|,|a-b|}≥min{|a|,|b|}

C.min{|a+b|2,|a-b|2}≥|a|2+|b|2

D.min{|a+b|2,|a-b|2}≤|a|2+|b|2

(2014年浙江省数学高考理科试题第8题)

此题就是由平行四边形的对角线平方之和等于4条边平方之和这一结论类比成向量问题而来的.

(7)以变换设计命题.如代数式变换、图形变换、函数变换、方程变换、常量变量变换等.

图2

此题是依据三角形两边之和大于第三边而来，由立体几何中的三棱锥(如图2)构造出底边三角形的3条边.

如果把三棱锥的3条侧棱长和3个顶角变动一下，得到的3条边长就是另外形式了.但是大小关系仍然成立，可以得到新的命题.

再如，命题“已知二次函数f(x)=4x2-2(a-2)x-2a2-a+1，当x∈[-1,1]时至少有一个值c，使得f(c)>0，求a的取值范围.”就是由“对任意x∈[-1,1]恒有f(c)≤0，求a的值”正反转化而来.

有的则是从解题思维的正反转换来设计命题.

例12设k∈R，关于x的方程x4-2kx2+k2+2k-3=0有实根，求其实根的取值范围.

(8)以小题综合成大题，或以大题分解成小题设计命题.

(9)以相关知识的联系和组合设计命题.

3 命题设计的注意点

设计数学命题相对于其他学科的命题，有其自身学科的特点，在命题时应重视并体现.

要体现数学学科的特点——精简、明确、严谨;要把握核心内容、主干知识、基本方法(通性通法)、典型问题;要反映数学思想、数学方法、数学能力和学习数学的素质潜能;要区分3类题型的特性，在解题方法、能力、技巧和时间、难度上有所区别;要考虑综合解答题的解题过程、步骤、中间环节对整体解决和结论的影响，重视分题意义和前后小题的关联.比如前面一个数据算错，是否会影响整体解答.如果是考查数学思维方法能力的命题，由于前面计算粗心而使后面即使思维方法正确也无法继续解答的，这种命题设计就难以达到考查数学思想方法能力的目的.

4 编制试卷

命题设计是单个的，要把设计好的命题编织成一份试卷，是综合设计的过程.

(1)明确试卷测试的目的，根据测试目的，设计试卷内容和要求.一般来说，日常教学中有3类试卷.

第1类，单元内容检查.重点在于检查本单元的知识、方法和相应数学思想能力的掌握，根据单元的教学要求设计，不必在于难易度.考后可针对相应问题分析、点评、反馈，以查漏补缺、巩固提高.

第2类，学期阶段评估.如期中期末考、毕业考等.这是一类学业水平等级评估考核，考查相关知识、思维、方法、能力等，根据教学目的要求设计试卷.设计时要考虑相关的因素，如学生情况，测试时间、难度系数、考核各档次的成绩、合格分和通过比例等.

第3类，模拟选拔训练.在现在的高考制度下，针对高考选拔的模拟测试训练是必不可少的，这类试卷的目的就是根据教学目的、高考要求,反复训练，巩固提高，适应高考.设计时要准确把握高考要求、高考信息，体现主干知识、重要内容、数学思想、数学能力、数学方法及灵活综合运用的技能.

(2)编制试卷应考虑的因素.

①明确设计的是哪一类试卷;

②把符合这类试卷的相应命题按知识、方法、题型和难易度分类、分层、分档;

③按考试时间、考试要求、知识分布、题量结构、分值比例，在分好类的命题中选择相应题目编制试卷;

④编制好后，试做一遍，对完成时间、评卷标准、难点、易错点和分数档次等有所预测;

⑤注意题号顺序、难度梯次、知识点、面覆盖和避免重复;

⑥谨慎使用偏题、怪题和技巧特别的难题;

⑦控制好计算量、讨论量、作图量和解答过程中书写的时间量.

有些所谓的好题，往往是方法巧妙、思维新颖、能力要求高、容易犯错类的命题，如果把教师认为的这类好题过多地编制在同一份试卷中，往往是一份过难的、不恰当的试卷，从而不能很好地体现这份试卷考查的目的和意义.

命题涉及的内容还有许多，命题过程实际上是数学教学的分析、研究、总结过程，也是数学教学的重要环节和组成部分.我们可以把某份高考试卷当做范本，认真透彻地分析研究，从中学习并体会命题的方法和意义.