一种稳健的格基规约非线性预编码算法

康桂华，潘坤贝

（河海大学物联网工程学院，常州213022）

·微机网络与通信·

一种稳健的格基规约非线性预编码算法

康桂华，潘坤贝

（河海大学物联网工程学院，常州213022）

为解决THP预编码在信道矩阵不理想情况下误码率较高的问题，提出了一种在MMSE准则下改进的格基规约THP预编码算法。该算法在原有格基规约THP算法基础上进一步改造用户信道矩阵，使其尽可能满秩，从而增加系统鲁棒性。仿真结果表明，该算法相对原有算法在10dB信噪比之后误码率性能得到提升，性能提升了约3dB。

模代数预编码；格基规约；最小均方误差

1 引 言

近年来，预编码技术被广泛应用于无线通信领域中大容量和高可靠性传输等方面。预编码是一种在发送端利用已知信道状态信息，对发送数据进行预处理，使其能够适应相应信道环境的技术。预编码技术分为线性预编码和非线性预编码两大类，尽管线性预编码无需求模等非线性处理，具有实现简单、复杂度低等优点，但是它没有充分挖掘信道潜力。非线性预编码一定程度上补足了线性预编码的弱点，使系统在信道容量上逼近理论值。

非线性预编码有脏纸编码，THP（Tomlinsonharashima precoding）预编码等。但脏纸编码算法复杂度高，实现困难，而THP预编码在性能和复杂度上具有较好折中。因此在发送端已知信道状态信息的情况下，THP预编码常用于系统性能提升。

THP预编码主要包括连续干扰消除和模运算两部分［1］。文献［2］提出在降低误码率性能方面，基于MMSE（最小均方误差）准则比基于ZF（迫零）准则下的THP预编码算法性能表现良好。已有文献［3］提出将格基规约与THP预编码结合相比一般THP预编码性能进一步提升。文中提出的预编码算法是在MMSE准则下，以文献［3］算法为基础，同时对用户信道矩阵进行处理和向量选择，最后对该方案的性能进行仿真分析。

2 系统描述

假设基站有Nt个发送天线，同时发送数据给K（K≤Nt）个分布在基站周围的用户，其中每一个用户配备一个接收天线。这里假设信道为随机高斯信道，且不考虑信号散射。非线性预编码下的MIMO（Multi－Input Multi－Output）系统结构图如图1所示。

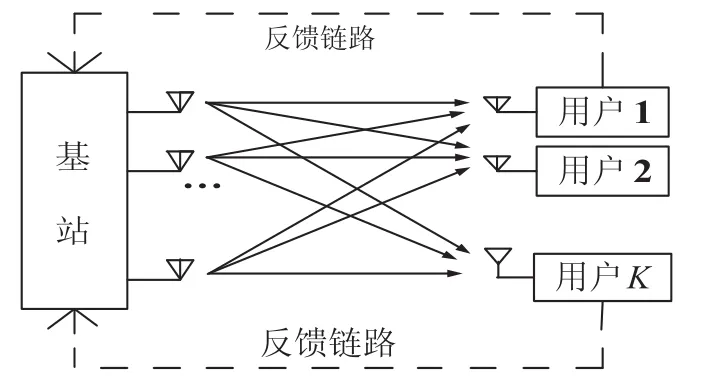
图1 MIMO系统结构图

采用矩阵表示法［4］，则接收信号可以用经典的MIMO模型表示为：

式（1）中y（t）＝［y1（t），…，yK（t）］H包含用户的接收信号，x（t）＝［x1（t），…，xNt（t）］H包含基站天线发送信号，n（t）＝［n1（t），…，nK（t）］H包含用户接收信号伴随的高斯随机噪声，白高斯随机噪声方差为，且，H＝［hk，l］是K×Nt的信道矩阵，hk，l是其第k行l列的元素，满足标准高斯正态分布。不失一般性，假定信道矩阵在确定时间内是恒量，且信道之间相互独立。

3 预编码方案设计

3.1 传统THP预编码

传统THP预编码［5－6］系统模型如图2所示。

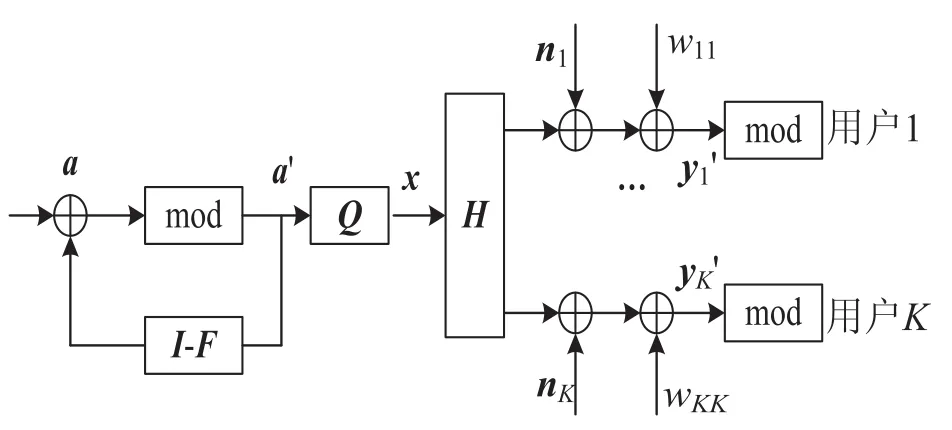
图2 传统THP预编码方框图

图2中发送信号经过M－QAM调制被映射成信号向量a，信号向量经过求模（mod）和反馈运算被约束在边长为的正方形区间内，其中m表示完全平方数。

求模步骤如下：

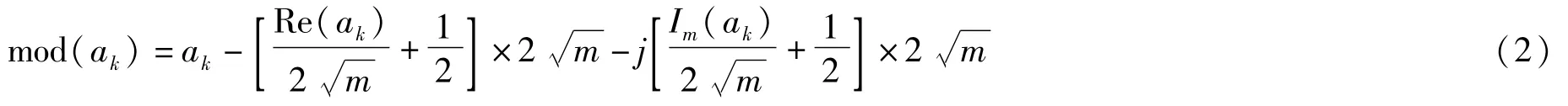
式（2）中，ak表示信号向量，Re（.）表示取实部，Im（.）表示取虚部，?.」表示向下取整。

反馈和求模递归形式为：

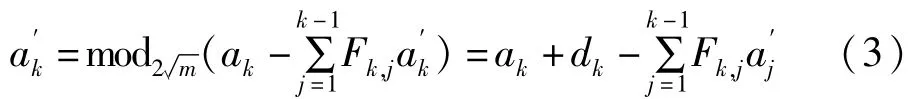
式（3）中Fk，j代表反馈矩阵F第k行j列的元素，。

式（3）矩阵表达式为：

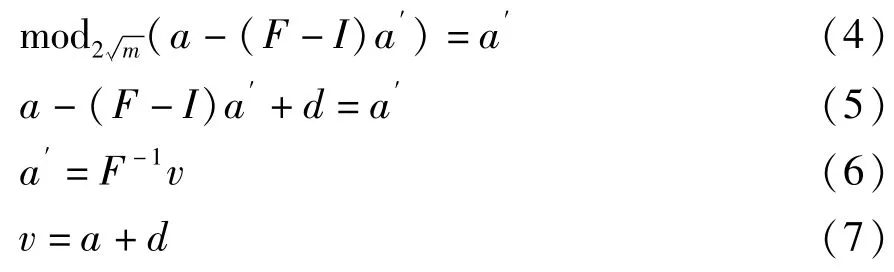
式（7）中v代表等效信号向量。

信号向量a经过反馈和求模处理之后获得发送向量a′，结合式（6），由图2得到

式（8）中y′表示用户的接收信号向量，W表示加权矩阵，Q表示前馈矩阵，H表示信道矩阵，H可进行QR分解，使其满足：

式（9）中U为酉矩阵，可以赋给Q，V为上三角矩阵，V矩阵中对角线元素的倒数作为对角矩阵赋给W，反馈矩阵F由加权矩阵W与上三角矩阵V的乘积得到，即：接收端再经过与发送端一致的求模运算即可恢复出信号向量。

3.2 改进的格基规约THP预编码

格基规约（LR）近年来在通信领域已得到广泛应用［7］。设B＝（b1，…，bn）是一组线性无关向量，CZn代表复整数集合，格L由式（11）定义［8］。

如果T为幺模矩阵，那么B和BT产生相同的格，即满足：

格基规约优化格的产生矩阵，使得矩阵BT产生的格图相比矩阵B产生的格图更加正交且缩短了欧氏距离，从而使经过格基规约操作后的等效矩阵奇异性得以改善。

格基规约THP算法应用幺模矩阵T改善信道矩阵奇异性，等效为：

式（13）中H～为经过改善后的信道矩阵，由于格基规约改善了信道矩阵，使它更加正交，减少了用户间的干扰，因此将格基规约与THP预编码相结合比不结合格基规约的预编码方案在降低误码率性能方面得到了提升。

在进行THP预编码时，基于ZF准则下的THP预编码文献［9］已描述；所谓MMSE准则就是使接收端接收到的数据与发射端发送的数据之差最小，即：

式（7）、（8）代入式（14）得到：

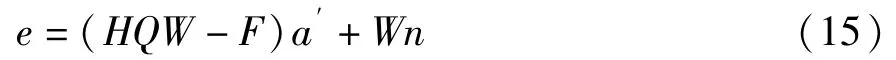
式（15）需满足一定的约束条件，即：

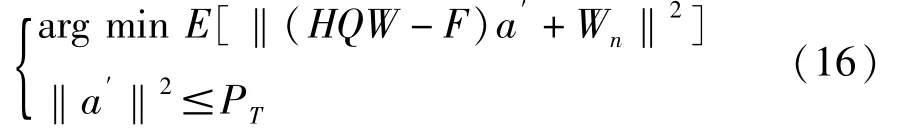
式（16）中，PT为总的发送功率。根据正交原理，最小均方误差满足：

式（8）、（14）代入式（17）得到：

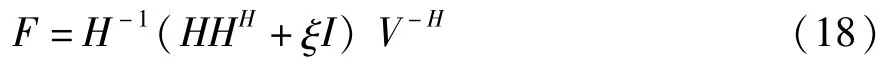
由式（18）可见基于MMSE准则下的预编码方案引入了ξI，综合考虑到了天线间干扰和噪声影响。从整体来看，发送基于MMSE准则的预编码方案要优于发送基于ZF准则的预编码方案，因此文中提出的算法就是在MMSE准则下进行的。

式（9）提到对信道矩阵H进行QR分解，已知式（10），即：

因此矩阵H的构成决定了矩阵V的构成，矩阵V影响了反馈矩阵F及加权矩阵W，进而影响了整个预编码方案性能。

由矩阵论知识可知，当矩阵V对角元素值趋于0时，会使矩阵F和矩阵W的构成不稳定，由式（8）知，这会严重降低THP预编码方案的干扰移除能力。要避免这种不良情况的发生，需使矩阵V对角元素值接近1，然而通常情况下，不理想的信道矩阵H会导致矩阵V对角元素值接近0。可见，传统格基规约THP预编码算法使信道矩阵奇异性得以改善，但并未满足矩阵V对角元素值接近1这一条件。基于此，文中提出了一种改善信道矩阵的方案，通过再次对信道矩阵H进行处理，使矩阵V的对角元素值接近1，提高了THP预编码方案的干扰移除能力。

具体处理过程如以下所示。

信道矩阵H＝［H1，...，HK］T；令

根据施密特正交原理有：

发送端从A0中选择具有最强信道向量的用户作为初始用户［10］，即：

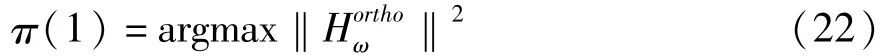
其中A0＝｛1，2，…，K｝，ω∈A0，π（1）代表初始用户序号。

当第i个用户选择后，第i＋1个用户选择规则如下：

其中ω∈Ai，j，i满足1≤j≤i，ε是用来限定不同用户信道向量空间最大相关度的参数，因为这里选择具有最强信道向量的用户作为初始用户，所以通常情况下Ai非空，故不用考虑ε的选择。

根据线性代数理论，发送端通过以上过程可以构造出一个满秩的信道矩阵H。

改进后的格基规约THP预编码系统模型如图3所示。

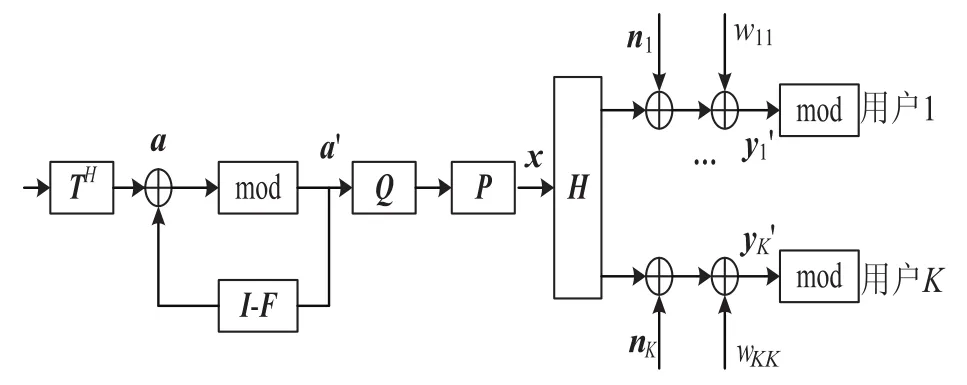
图3 改进后的格基规约THP预编码方框图

图3中TH代表格基规约算法矩阵，P是文中提出的用户信道矩阵处理和向量选择算法矩阵。通过发送端的预处理，构造出一个满秩的等效信道矩阵：

式（25）使矩阵V的对角元素值接近1，改善了传统格基规约THP预编码算法式（13）中由于信道矩阵不理想而导致V对角元素值趋于0的情况，从而增加了系统鲁棒性。

4 仿真结果与分析

在下行链路仿真中，假定基站有4个发射天线，发射天线发送信号功率归一化为1，基站周围分布着4个用户，每个用户有1个接收天线，调制方式为4－QAM调制，采用4×4MIMO系统，仿真次数设为10000，MIMO信道采用随机高斯信道，分别对ZF准则下的THP预编码、MMSE准则下的THP预编码和MMSE准则下的传统格基规约THP预编码以及改进的格基规约THP预编码进行仿真。

从图4的仿真结果看，出对于两种基于不同准则的THP非线性预编码来说，MMSE准则下的预编码考虑到噪声对系统的影响，在设计预编码矩阵时进行相应处理；而ZF准则下的预编码虽然在接收端无需通过复杂的处理即可通过解调获得原始的发送信号，但放大了噪声。因此MMSE准则相比ZF准则下的THP预编码，虽然牺牲了一定的复杂度，但并没有放大噪声，整体性能要优于ZF准则下的预编码，且性能提升了约2dB。MMSE准则下的传统格基规约THP预编码相比同一准则下的非格基规约THP预编码在10dB信噪比之后性能提升。

图4 传统格基规约THP预编码与非格基规约THP预编码误码性能比较

从图5仿真结果可以看出，文中所提出的MMSE准则下改进的格基规约THP预编码相比同一准则下传统格基规约THP预编码在10dB信噪比之后性能得到提升，性能提升了约3dB。由于本算法改善了高信噪比时信道状态不稳定的情况，因此在高信噪比时文中所提出的算法能达到较好的降低误码率目的。

5 结束语

改进的格基规约THP预编码方案结合格基规约并对用户信道矩阵进行处理和向量选择，构造出一个满秩的信道矩阵，使原有算法更加稳定，并通过仿真验证了本算法相比原有算法在降低误码率性能方面具有优越性，从而进一步逼近了MIMO系统容量理论值。

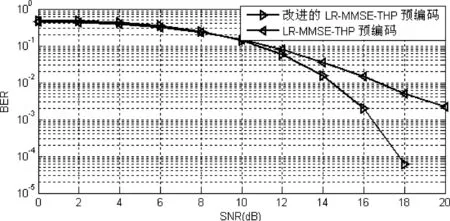
图5 改进后的格基规约THP预编码与改进前的格基规约THP预编码误码性能比较

［1］H Harashima，H Miyakawa.Matched－transmission technique for channels with intersymbol interference［J］.IEEE Trans on Commun，Aug.1972，20：774－779.

［2］Jia Liu，Witold A.Krzymien，Improved Tom linson－Harashima precoding for the downlink of multi－user MIMO systems［J］.Can.Elect.Comput.Eng.，Summer 2007，32（3）：133－144.

［3］Clemens Stierstorfer and Robert F.H.Fischer，Lattice Reduction Aided Tomlinson Harashima Precoding for Point－to－Multipoint Transmission［C］.AEU Int.Electron.Commun，2005.

［4］Fischer，R FH，Windpassinger C.Real－vs Complexvalued equalization in V－BLAST systems［J］.Electronics，Marz 2003，39：470－471.

［5］Fischer，R.F.H.，et al.Space－time transmission using Tom linson Harashima precoding［C］.ITG FACHBERICHT，2002：139－148.

［6］Michael Joham，Johannes Brehmer，Andreas Voulgarelis，Wolfgang Utschick.Multiuser Spatio Temporal Tomlinson Harashirna Precoding for Frequency Selective Vector Channels［J］.ITG Workshop on Smart Antennas，2004：208－215.

［7］E Agrell，T Eriksson，A Vardy，et al.Closest point search in lattices［J］.IEEE Trans on Inf.Theory，2002，48：2201－2214.

［8］DWubben，D Seethaler，JJalden.Lattice Reduction［M］.IEEE Signal Processing，2011，20（4）：70－91.

［9］Q Spencer，A Swindlehurst，M Haardt.Zero－forcing methods for downlink spatial multiplexing in multiuser MIMO channels［J］.IEEE Trans on Signal Processing，February，2004，52：461－471.

［10］Saeed Moradi，Glenn Gulak.A Robust RAM－THP Architecture for Downlink Multiuser MISO Transmission with User Scheduling［J］.IEEE Trans on Commun，2011：334－339.

A Robust Nonlinear Precoding Algorithm Based on Lattice Reduction

KANG Gui－hua，PAN Kun－bei
（College of Internet of Things Engineering，Hohai University，Changzhou 213022，China）

An improved THP precoding algorithm with lattice reduction under MMSE criterion is proposed in this paper，which intends to solve the problem of high bit error rate when the channelmatrix is in bad condition.The user＇s channel vectormatrix is furthermodified by this algorithm，which is based on the original THP precoding algorithm with lattice reduction，and this proposed onemakes the channel matrix full rank as possible and increases the robustness of the system.Simulation results show that the proposed algorithm can improve the BER performance and make the signal－to－noise 3dB higher than the original one after 10dB SNR.

Tomlinson－harashima precoding（THP）；Lattice Reduction（LR）；Minimum Mean Square Error（MMSE）

10.3969／j.issn.1002－2279.2014.06.008

TN929.5

：A

：1002－2279（2014）06－0022－04

康桂华（1963－），男，汉族，江西吉安人，博士，副教授，硕士生导师，主研方向：无线移动通信。

2014－03－07