一种改进的NAS-RIF水下图像盲复原算法

曲李虎，林善明

（1.河海大学物联网工程学院，常州213022；2.河海大学传感网与环境感知重点实验室，常州213022）

一种改进的NAS-RIF水下图像盲复原算法

曲李虎1，2，林善明1，2

（1.河海大学物联网工程学院，常州213022；2.河海大学传感网与环境感知重点实验室，常州213022）

提出一种基于空域自适应加权因子的NAS-RIF图像盲复原算法，算法通过在原NAS -RIF算法代价函数中引入空域自适应加权因子，以改善图像复原的逼真和平滑。实验结果表明，改进后的算法信噪比改善增益可以提高2.39dB，复原后图像细节和清晰度有了一定程度的改善。

图像复原；非负支撑域受限递归逆滤波算法；加权因子；正则化；

1 引 言

经典的图像复原算法如维纳滤波、逆滤波等是基于退化系统的点扩散函数PSF已知的前提下进行的，而在实际水下场景应用中退化系统的PSF是传感器、光学衍射、水下环流等因素共同作用的结果，通常无法获知，所以经典图像复原算法不适合应用于此场景中。图像盲复原方法不依赖于图像的先验知识，也不需要准确预知退化系统的PSF，因而在实际水下场景中得到了广泛应用。

目前最具有代表性的图像盲复原算法有迭代盲目反卷积［1］（Iterative Blind Deconvolution，IBD）、递归逆滤波盲目反卷积算法［2］（Nonnegativity and Support constraint Recursive Inverse Filtering，NASRIF）。IBD算法缺乏可靠性，解的唯一性和算法收敛性不能确定，而且对于PSF的初始估计值比较敏感，复原效果通常不佳。

NAS-RIF算法的计算复杂度较低，具有较好的收敛性，而且复原算法仅需预知退化图像的支撑域范围，其代价函数为凸函数［3］，可以保证解的唯一性。但NAS-RIF算法在低信噪比时会带来噪声放大现象［4］，从而导致图像复原效果不佳。针对上述缺点，提出一种基于空域自适应加权因子的NAS-RIF图像盲复原算法。

2 NAS-RIF原理简介

NAS-RIF算法是一种基于递归滤波器的盲复原算法，算法模型如图1所示。图中，g（x，y）为退化图像，u（x，y）是逆滤波器，表示估计图像，NL是非线性函数，功能为约束图像的支撑域范围，是满足NL约束条件在真实图像空间上的投影，e（x，y）为的差值。

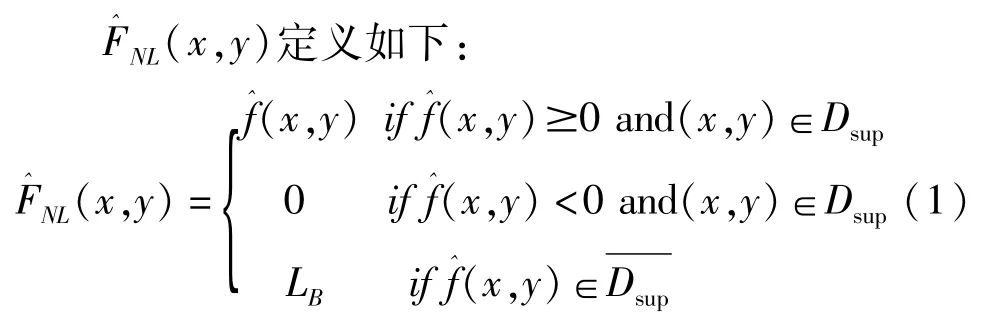
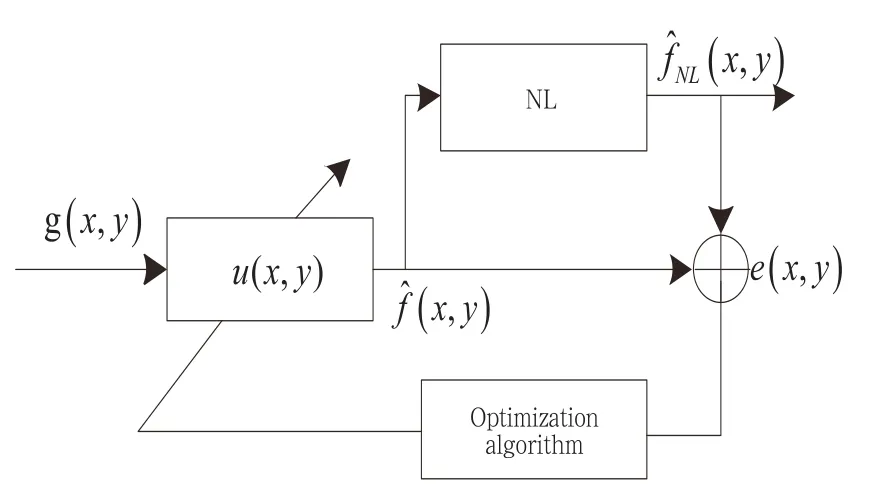
图1 NAS-RIF算法模型

上式中Dsup为图像的目标支撑域，为背景区域，LB为背景区域像素均值。

NAS-RIF算法原理：退化图像g（x，y）通过一个二维可变系数的滤波器u（x，y）进行卷积运算得到原始图像的估计值，估计图像通过非线性约束函数映射得到投影图像，然后通过与的差值来动态调整滤波器系数e（x，y），经过多次迭代可以得到复原图像。在复原过程中，NAS-RIF算法的代价函数定义为：

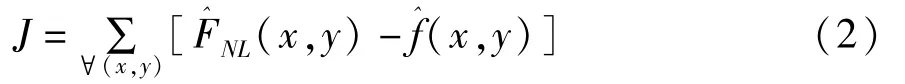
上式等价于：

其中，sgn（f）为符号函数，若逆滤波器u（x，y）出现系数全为零的解，此时复原出图像是全黑的，复原出的图像没有任何意义，所以需要在代价函数中增加关于u（x，y）的约束项来避免此种情形，常用的约束项为，修正的代价函数J为：

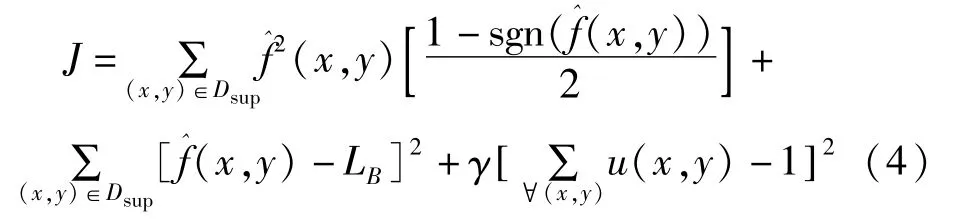
其中，γ为常数，当背景像素不为全黑时γ＝0，反之，γ≠0，通常为了减小代价函数，取值不宜过大。NAS-RIF算法的代价函数为凸函数，因此存在全局最优解。

3 改进NAS-RIF盲复原算法原理

NAS-RIF算法［5-7］在低信噪比时会造成噪声放大，从而导致图像复原效果不佳。而水下图像通常具有信噪比较低、噪声干扰严重、图像对比度较低等特点，会加剧NAS-RIF算法的性能退化。如果在原始的NAS-RIF算法代价函数中增加空域自适应加权因子和正则化约束项，便可以很好的改善图像复原效果，改进后NAS-RIF算法的代价函数表达式为：

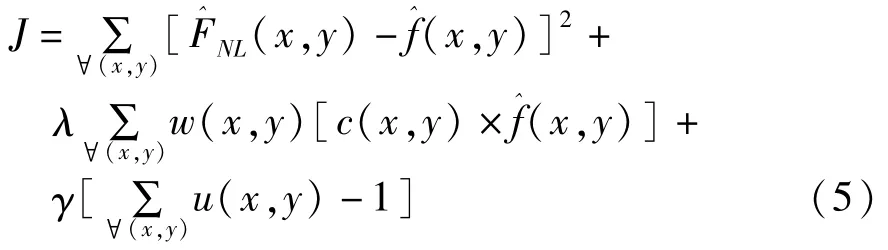
上式中，w（x，y）、c（x，y）、λ分别为空域加权因子、正则化算子和正则化参数，c（x，y）选取高通滤波器，算子的支持域为3×3，支持域太大容易造成边缘振铃效应，故c（x，y）选取为：

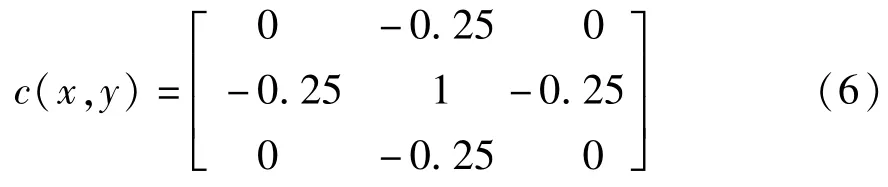
λ可以通过图像的局部方差与图像的噪声方差（Noise Variance，NV）计算获得，选取方法为：

mg（x，y）为退化图像的局部均值，数学表达式为：

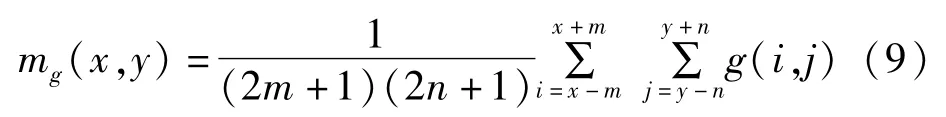
图像的局部方差和均值通过矩形窗口计算得到，m、n取值为m＝n＝1。图像噪声方差估计为：

空域加权因子w（x，y）选取的表达式为：

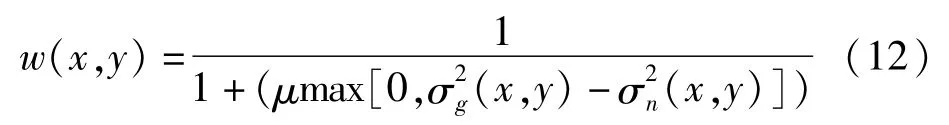
参数μ一般与图像具有较大的相关性，通常选取为：

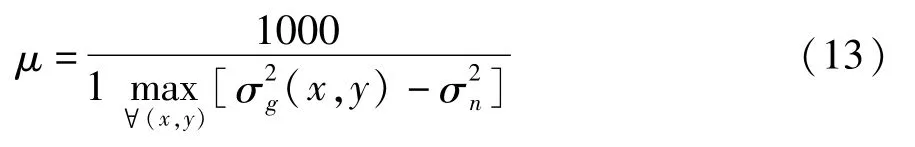
4 实验结果与分析

如何评估一个图像复原算法的效果是一个未解决的难题，目前还没有找到一个客观的评判标准能与人的主观判据相一致。在图像复原的算法研究中为了定量分析评价复原效果，常用的评价准则为图像信噪比增益：

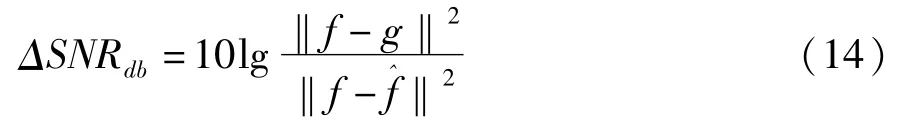
其中f是未退化的图像，g是退化图像，f＾为复原后图像，ΔSNR越大表明复原后的图像越接近原始未退化图像，从而表明算法的性能越好。对于实际的图像复原问题，信噪比改善增益是无法计算得到的，因此上述准则仅用于模拟实验分析，更多的利用人的主观视觉分析。

由于实际环境中获取的水下光学图像，其原图像和退化函数的参数无法预知，所以只有对图像标准库中的circuit图像进行测试，分析所提出的算法性能。图2（a）为原图像，2（b）为模糊图像，退化模型为线性移动降晰函数，降晰函数长度d＝10，其机理是图像获取时水下摄像机和场景之间存在均匀线性运动，图2（c）为采用NAS-RIF盲卷积复原的图像，图2（d）为采用改进算法复原的图像。

图2 普通图像复原实验

由图2可以看出，原始的NAS-RIF算法复原效果图有轻微的模糊效应，改进算法复原图像较为清晰，主观视觉优于原始算法，采用客观评价指标进行定量分析，可以看出改进的算法信噪比改善增益可以比原始NAS-RIF算法高出2.39dB。

表1 改进算法与NAS-RIF算法复原对比

对真实水下图像进行实验，如图 3所示，图3（a）为原图像，原始NAS-RIF算法复原如图3（b）所示，改进算法复原图像如图3（c）所示。

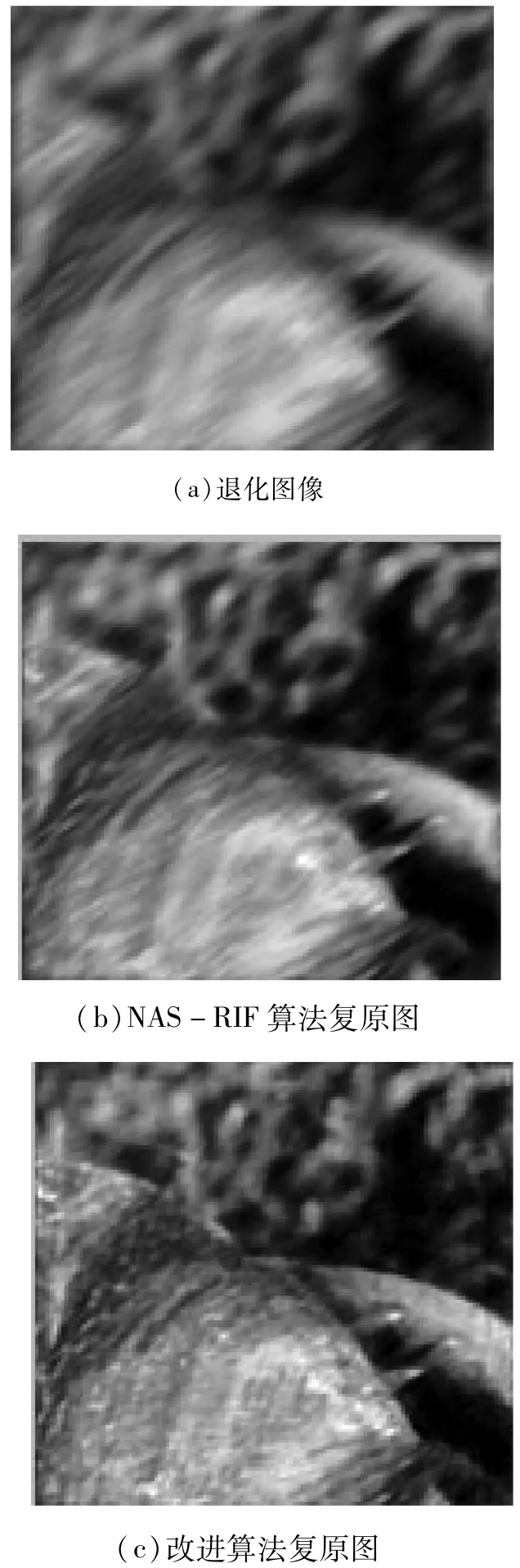
图3 水下图像复原实验

从图3中可以看出，改进的NAS-RIF算法可以有效改善复原后图像的效果，复原后的图像细节较为清晰，算法可以较好的抑制噪声对水下图像复原的影响，复原效果优于原始的NAS-RIF算法。

5 结束语

针对原始的NAS-RIF算法在图像低信噪比时会造成噪声的放大，从而导致算法性能急剧恶化的缺点，提出一种改进的NAS-RIF图像盲复原算法，在代价函数中引入了空域自适应加权因子和正则化约束项来改善复原图像效果。实验结果表明，所提出的算法可以改善水下退化图像质量，复原图像的客观质量和主观视觉效果都有了明显改善。

［1］Ayers Gr，Dainty JChristopher.Iterative blind deconvolution method and its applications［J］.Optics letters，1988，13（7）：547-549.

［2］Kundur Deepa，Hatzinakos Dimitrios.A novel blind deconvolutionscheme for image restoration using recursive filtering［J］.IEEE Transactions on Signal Processing，1998，46（2）：375-390.

［3］KUNDUR D.Blind deconvolution of still images using recursiveinverse filtering［D］.M.A.Sc thesis，University of Toronto，Department of Electrical and Computer Engineering，1995.

［4］黄德天，吴志勇.基于非负支撑域受限递归逆滤波的自适应图像盲复原［J］.光学精密工程，2012，9（20）：2076-2086.

［5］张航，罗大庸.图像盲复原算法研究现状及其展望［J］.中国图象图形学报，2004，9（10）：1145-1152.

［6］郭永彩，王婀娜，高潮.空间自适应和正则化技术的盲图像复原［J］.光学精密工程，2008，16（11）：2263-2267.

［7］KUNDER D，HATZINAKOSD.Blind image deconvolution［J］.IEEE Signal Processing Magazine，1996，13（3）：43-64.

An Im proved NAS-RIF Blind Image Restoration Algorithm

QU Li-hu1，2，LIN Shan-ming1，2
（1.Internet of Things Engineering College，Hohai University，Changzhou 213022，China；2.Key Laboratory of Sensor Networks and Environmental Sensing，Hohai University，Changzhou 213022，China）

This paper presents an adaptiveweighting factor spatial NAS-RIF blind image restoration algorithm，the cost function spatial adaptive weighting factor is introduced in the original NAS-RIF algorithm to improve image restoration realistic and smooth.The experiment results show that the improved algorithm can improve the signal to noise ratio improvement gain 2.39db，and the detail and clarity of the restored image have improved to some extent.

Image restoration；Non-negativity and Support constraint Recursive Inverse Filtering algorithms；Weighting factor；Regularization

10.3969／j.issn.1002-2279.2014.04.020

TP391.4

：A

：1002-2279（2014）04-0062-04

曲李虎（1987-），男，江苏连云港人，硕士研究生，主研方向：信号检测与处理。

2013-10-28