六角形格林函数节块法

安 萍，姚 栋

(中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610041)

近二十多年来，求解多维中子扩散方程的粗网格计算方法得到广泛发展，其中矩形先进节块方法的发展和应用尤为成功。Lawrence等[1-2]成功发展了矩形节块格林函数方法(NGFM)，并通过大量例题验证了理论及程序的正确性和高效性。随着采用六角形几何的快堆的发展和俄罗斯VVER型压水堆的应用，六角形节块法的研究也日益得到重视，将先进矩形节块法推广到六角形节块有非常重要的意义。

Chao等[3]研制的六角形节块扩散程序ANC-H是目前公认的国际上精度最高的六角形节块程序。程序采用保角变换思想将六角形几何变换为矩形几何。本文采用该保角变换将六角形节块变换为矩形节块，对变换后的矩形节块扩散方程进行横向积分。并应用第二类边界条件的格林函数法，建立六角形节块各表面净中子流为未知量的空间耦合方程，采用剩余权重源迭代方法进行求解。研制三维多群六角形格林函数堆芯程序NACK，采用大量基准题对其进行验证，并与国际上相应程序的计算结果进行比较。

1 保角变换

保角变换是一种特殊映射，它保持任一点邻域内变换前后的伸缩性和旋转角不变，并保持角的定向。存在六角形到矩形的保角变换因子f[3]。图1示出变换前后对应点的关系，其中a和b为矩形长和宽。拉普拉斯算子在保角变换下形式不变，即：

(1)

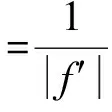
图1 六角形节块到矩形节块的保角变换

三维六角形节块扩散方程(式(2))经保角变换为矩形节块扩散方程(式(3))。

(x,y,z)+

(2)

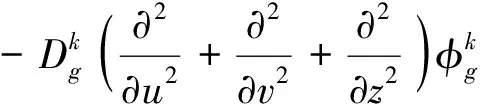
(3)

±

(4)

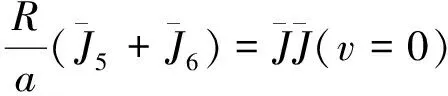
(5)

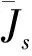
2 六角形格林函数程序模型

对式(3)沿v、z两个方向积分，得到横向积分方程：

(6)

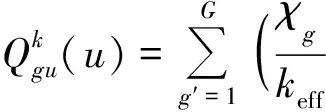
(7)

(8)

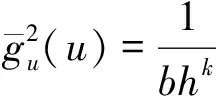
(9)

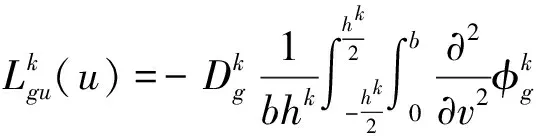
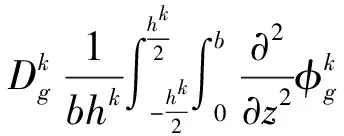
(10)

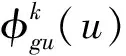
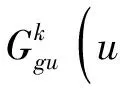
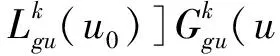
(11)

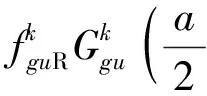
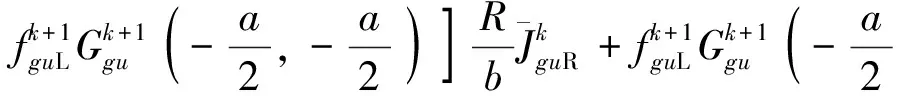
(12)

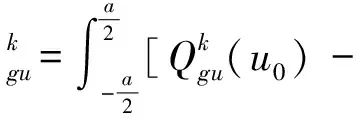
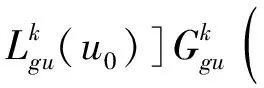
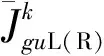
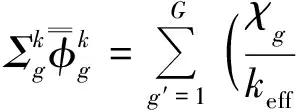
(13)

采用剩余权重法求解上式，将偏中子通量密度和横向泄漏项在节块内用二阶Legendre正交多项式Pn-1(u)(n=1,2,3)展开，有：

(14)

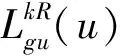
(15)

则中子源项为：

(16)

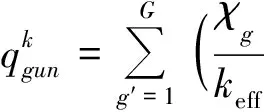
3 数值验证

3.1 不带反射层的二维VVER-1000基准题

不带反射层的二维VVER-1000基准题[4]的堆芯有8圈燃料组件，全堆芯共插25束控制棒，堆芯1/6旋转对称，组件的对边距为23.6 cm，燃料组件外的反射层未参与计算。采用两种反照率β=0.6和0模拟“真实边界”和“真空边界”。

图2分别示出在β=0.6和0两种情况下，NACK程序计算所得的有效增殖因数和堆芯归一化功率分布(参考值由细网差分程序DIF3D-FD[4]计算得到)。表1为各程序对该基准题计算结果的比较。其中，AFEN程序由Cho等[5]研制，采用解析基函数节块展开法；HEXNOD23程序由Grundmann[6]开发，也采用解析节块法，将中子通量密度展开成三角函数和贝塞尔函数乘积；SIXTUS-2程序是Arkuszewski[7]基于对称性原理开发的六角形解析节块程序。计算结果显示，NACK计算结果良好，与ANC-H精度相当。

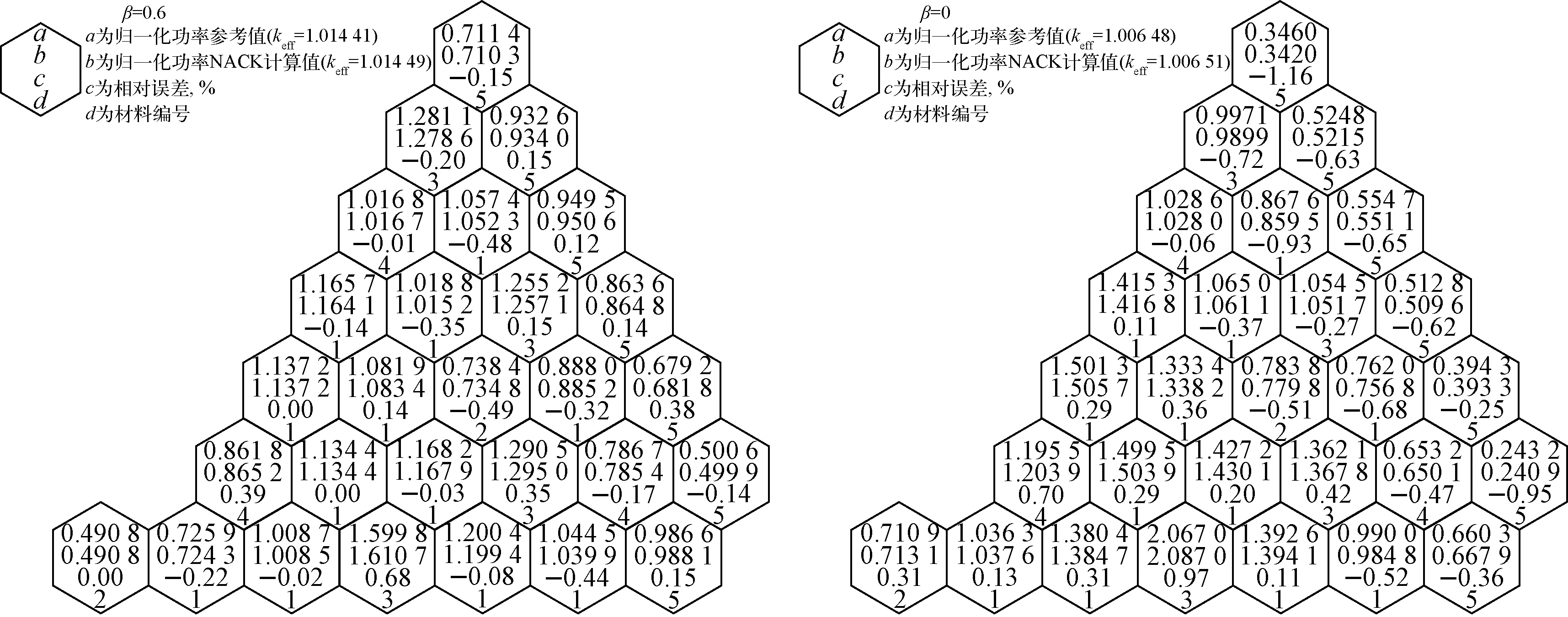
图2 NACK计算的不带反射层VVER-1000基准题的堆芯功率分布

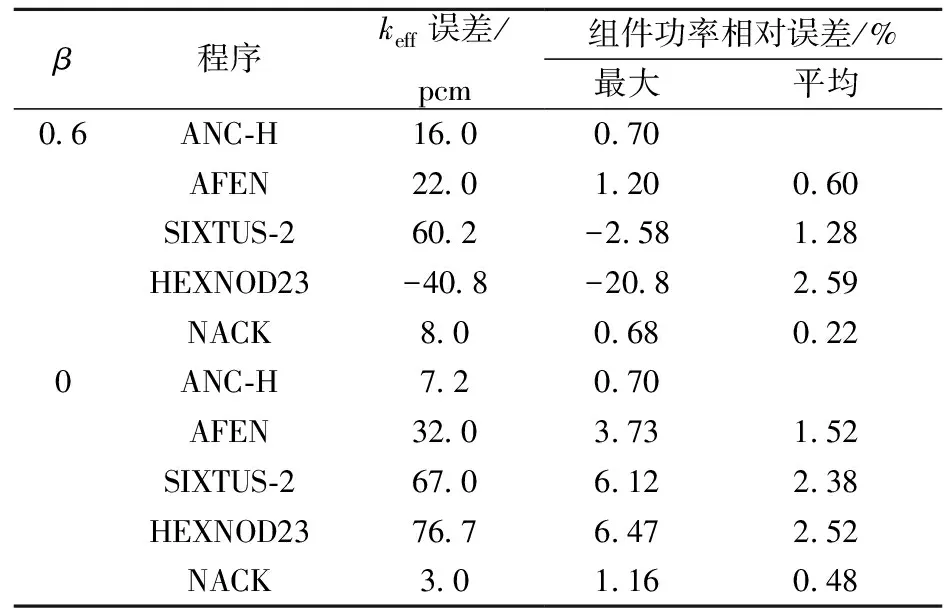
表1 不带反射层VVER-1000基准题各程序计算结果的比较

3.2 三维VVER-440基准题

三维VVER-440基准题[8]是二维VVER-440基准题的扩展。堆芯高度为250 cm，在堆芯的顶部和底部分别加25 cm厚的反射层。另外，堆芯内的所有控制棒均上提到堆芯中部。堆芯外边界全部为真空边界。

图3为NACK程序计算所得的有效增殖因数和堆芯归一化组件功率分布(参考值由细网差分程序DIF3D-FD[4]计算得到)。表2为针对该基准题各程序计算结果的比较，可看出，NACK程序与这些程序的计算精度相当。其中，GTDIF-H是张少泓[8]利用六角形几何对称性和群论方法研制的节块法程序，GTDIF-H数据来自文献[8]，ANC-H和AFEN的数据来自文献[9]。

图3 NACK计算的三维VVER-440基准题的堆芯功率分布

3.3 带不连续因子的二维基准题

带不连续因子的二维基准题[10]有151个燃料组件，带水反射层，组件对边距22.4 cm。燃料组件含有UO2和MOX燃料。该堆芯的布置为1/12反射对称，采用零通量密度边界条件。

图4为程序NACK计算所得的keff和堆芯功率分布(阴影部分为MOX燃料)。其中，参考值是细网差分程序VENTURE的计算结果，是将每个六角形节块剖分成1 352个子节块计算得到的。表3列出各程序计算结果的比较(表中AFEN、HEXMED数据取自文献[11])。HANDF[10]为带不连续因子的解析节块法。

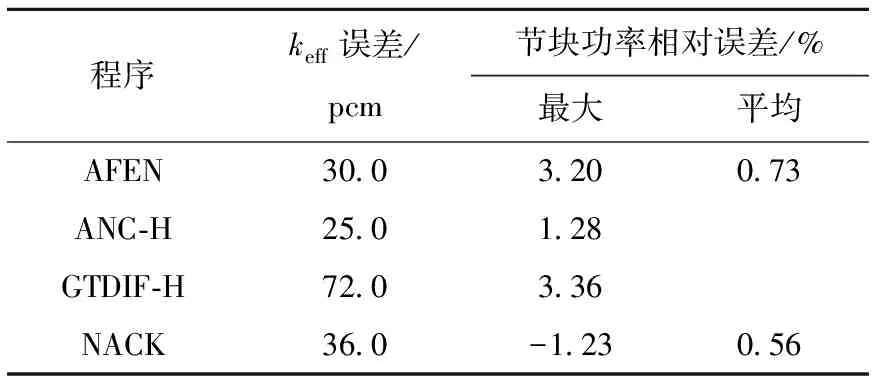
表2 三维VVER-1000基准题各程序计算结果的比较

图4 NACK计算的含不连续因子的基准题的堆芯功率分布

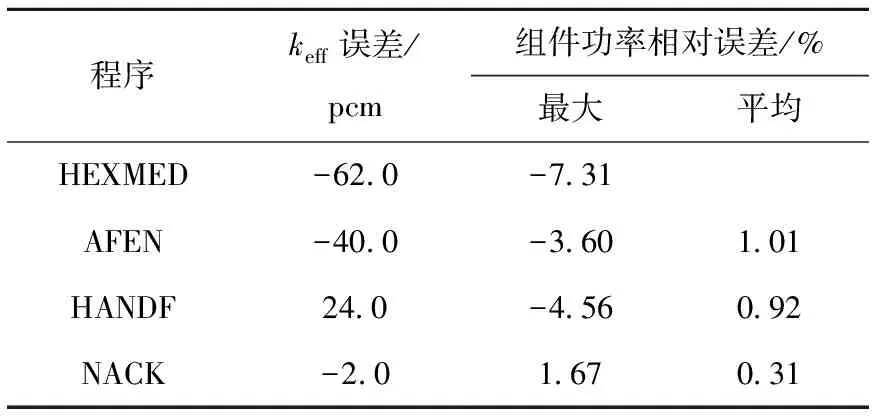
表3 带不连续因子的基准题各程序计算结果的比较

4 结论

本文根据保角变换思想和格林函数法，提出了新型带不连续因子的三维多群六角形节块方法模型，将格林函数节块法成功应用于六角形几何，并根据理论模型编制了三维多群稳态中子扩散程序NACK，通过基准题的计算，验证了理论模型和程序的正确性。下一步将实现NACK程序的加速计算和功率重构功能，并编制相应的时空动力学瞬态程序。

感谢上海交通大学赵荣安教授在程序模型研究中提供的帮助和指导。

参考文献：

[1] LAWRENCE R D. A nodal Green’s function method for multidimensional neutron diffusion calculations[D]. US: University of Illinois, 1979.

[2] 胡永明，赵险峰. 第二类边界条件先进格林函数节块法[J]. 清华大学学报：自然科学版，1998，38(4)：17-21.

HU Yongming, ZHAO Xianfeng. Advanced nodal Green’s function method on neumann boundary condition[J]. Journal of Tsinghua University: Science and Technology Edition, 1998, 38(4): 17-21(in Chinese).

[3] CHAO Y A, TSOULFANIDIS N. Conformal mapping and hexagonal nodal methods, Ⅰ: Mathematical foundation[J]. Nucl Sci Eng, 1995, 121(2): 202-211.

[4] CHAO Y A, SHATILLA Y A. Conformal mapping and hexagonal nodal methods, Ⅱ: Implementation in the ANC-H code[J]. Nucl Sci Eng, 1995, 121(2): 212-225.

[5] CHO N Z, KIM Y H. Extension of analytic function expansion nodal method to multi-group problems in hexagonal-Zgeometry[J]. Nucl Sci Eng, 1997, 126(3): 35-47.

[6] GRUNDMANN U. HEXNOD23: A two and three dimensional nodal code for neutron flux calculation of thermal reactors with hexagonal geometry, ZFK-557[R]. [S. l.]: [s. n.], 1985.

[7] ARKUSZEWSKI J J. SIXTUS-2: A two-dimensional multi-group diffusion code in hexagonal geometry[J]. Progress in Nuclear Energy, 1986, 18(2): 123-130.

[8] 张少泓. 六角形节块三维多群时-空中子动力学方程组的数值解法及群论在六角形节块方法中的应用研究[D]. 西安：西安交通大学，1997.

[9] CHO J Y, KIM C H. Polynomial expansion nodal method for hexagonal core analysis[J]. Tran Am Nucl Soc, 1995, 73(1): 179-185.

[10] 倪东洋，咸春宇. 应用不连续因子修正的六角形解析节块方法[J]. 核动力工程，2010，31(2)：1-5.

NI Dongyang, XIAN Chunyu. Analytic function expansion nodal method for hexagonal geometry corrected by discontinuity factors[J]. Nuclear Power Engineering, 2010, 31(2): 1-5(in Chinese).

[11] CHO N Z, NOH J M. Analytic function expansion nodal method for hexagonal geometry[J]. Nucl Sci Eng, 1995, 121(3): 245-253.