考虑性能退化和多级保障的核动力系统可用度分析

尚彦龙，蔡 琦，赵新文，赵宇光

(海军工程大学 动力工程学院，湖北 武汉 430033)

核动力系统在使用过程中，随着工作时间的增加，设备性能会不断发生退化，同时还会伴随随机故障的发生，即设备具有性能退化故障和随机突发故障的双重特性。核动力装置的维修保障通常采用三级维修机构，即基层级、中继级和基地级。核动力系统在任务周期内的故障，需视情况由基层级进行现场维修或返回基地由中继级或基地级实施维修。同时，基于对系统性能恢复的考虑，在其性能退化到一定程度时，中继级和基地级维修机构会对其进行预防性维修。因此，考虑性能退化和多级保障条件下的核动力系统可用度分析是较为复杂和困难的问题。

传统基于二元逻辑的可靠性分析方法仅关注设备成功与否，对考虑设备性能退化的系统可用度分析缺乏合适的评判依据和建模手段。对于发生性能退化的系统可用度分析，合适而有效的建模工具是基于多状态系统理论的可用度分析方法。目前，用于多状态系统可靠性或可用度分析的方法[1]主要有：1) 布尔模型的扩展方法；2) Monte-Carlo仿真方法；3) Markov过程方法；4) 通用发生函数(UGF)方法。其中，前两种方法在分析结构复杂和状态数目较多的复杂系统时存在建模和计算方面的困难。而Markov过程方法能用于描述因退化、失效和维修引起的设备状态改变，计算得到设备在相应状态下的概率。UGF方法利用发生函数的复合运算能量化设备性能和状态概率对系统性能和状态概率的影响，在多状态系统可靠性、可用度分析方面表现出较强的优势[2-3]。因此，针对该类问题，理论上可将二者相结合，对考虑退化和复杂维修条件下的多状态系统进行可用度分析。

基于以上考虑，本工作研究将通用发生函数理论与Markov过程方法相结合的方法，对考虑性能退化和多级保障条件下的核动力系统进行可用度分析。

1 基于UGF的系统可用度算法模型

采用UGF进行系统可用度分析时，描述系统性能分布的基本信息是各设备的性能分布向量gj、pj(j=1,2,…,n)和系统的性能结构函数Φ(G1,G2,…,Gn)，n表示组成系统的设备数目。任意设备j的性能Gj都有mj种不同的离散状态，各状态的性能值及相应的状态概率分别通过gj=(gj1,gj2,…,gjmj)和pj=(pj1,pj2,…,pjmj)表示。系统性能结构函数Φ建立了系统性能与各设备性能之间的函数关系，基于此可对复杂多状态系统进行可用度分析。

1.1 系统性能分布发生函数

基于UGF理论可得设备j的性能分布发生函数[2]：

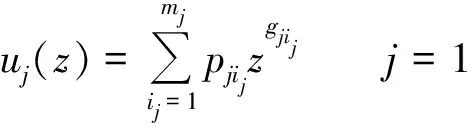
(1)

在系统各设备统计独立的情况下，对代表不同设备性能分布的发生函数作复合运算，即得到描述系统性能分布的系统发生函数：

U(z)=ΩΦ(u1(z),…,un(z))=

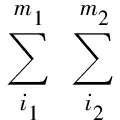
(2)

记为：

,2,…,M

(3)

式中：ΩΦ为复合算子符；z为辅助变量；u为设备的发生函数。

运算时，设备发生函数各项系数相乘，而指数的运算规则由Φ确定。对于由n个独立设备串联组成的多状态系统，其性能等于瓶颈设备(性能最低的设备)的输出性能值，其性能结构函数可表示为：

Φ(G1,G2,…,Gn)=ΩΦs(G1,G2,…,Gn)=

min(G1,G2,…,Gn)

(4)

n个独立设备组成的并联系统的性能等于各设备性能值之和，其性能结构函数可表示为：

Φ(G1,G2,…,Gn)=

(5)

式(1)～(5)中，设备各性能状态的概率可用可靠度或可用度代替，以分别用于系统的可靠性或可用性分析。

1.2 系统可用度计算模型

基于UGF的系统可用度计算，是在满足实际性能需求值w的情况下对式(3)各项系数进行条件求和[2]。即系统可用度A(w)可表示为：

A(w)=Pr{G(t)≥w}=

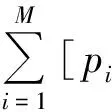
(6)

式中，1(·)为示性函数，当(gi-w)≥0时等于1，否则等于0。

2 考虑性能退化和多级保障的设备可用度模型

2.1 假设条件

假设条件为：1) 系统在完好状态和失效状态之间具有多个性能水平的退化状态，其对应不同的离散性能值；2) 系统可随机地从任何运行状态发生故障，实施的维修为最小维修；3) 状态转移时间服从指数分布；4) 设备当前性能状态可通过监测得到，且监测时间忽略不计；5) 忽略等待备件的延误时间。

2.2 模型建立

定义设备的以下状态。

Ai：性能状态，对应性能值为g，i=1,…，k,…，n(1≤k≤n-1)，n为性能状态总数目。其中：A1为设备的名义性能状态，An为故障状态，Ai(i=2,3,…,k,…,n-1)为中间性能状态；Ai′(i′=2,3,…，k+1)为可接受退化状态；Ai″(i″=k+2,k+3,…，n-1)为不可接受退化状态。

Bj：现场可修故障状态。其中，j=1,2,…,k+1。

Cj：现场不可修故障状态。

Dj：发生现场不可修故障，送达维修场所。

定义以下符号：λ2k-1为状态Ak到Bk的转移率；μ2k-1为状态Bk到Ak的转移率；λ2k为状态Ak到Ck的转移率；μ2k为状态Dk到Ak的转移率；σk为状态Ck到Dk的转移率；βk为状态Ak+1到Al的转移率，其中，l=1,2，…，k，1≤k≤n-1；αi为状态Ai到Ai+1的转移率，i=1,2，…，n-1。

根据以上描述，建立的系统状态转移图如图1所示。

由图1可知，核动力装置在服役过程中，随着工作时间的增加，设备性能将会由状态Ak(k=1,2,…,n-1)以转移率αk退化至下一降级状态Ak+1，或设备自身发生随机故障。设备发生随机故障时，或以故障率λ2k-1转移至现场可修故障状态Bk，或以故障率λ2k转移至现场不可修故障状态Ck，即设备状态的演绎是随时间缓慢退化和随机故障相结合的过程。

一般地，发生随机故障的主体通常为执行控制功能的电子器件或机械类易损件，这类故障修复后设备功能得到恢复但整体性能并不能得到改善。因此，可将这类修理视为最小维修(即设备性能和故障率恢复至故障前一时刻的状态)。设备进入故障状态Bk后，由于可现场维修，经基层级修理后会以维修率μ2k-1进入失效前状态Ak；发生状态Ck的故障模式，由于不能实施现场维修，设备将会以转移率σk返回修理场所即进入状态Dk，经中继级或基地级维修后以维修率μ2k转移至失效前状态Ak。

故障修复后的设备会在当前状态下继续演绎退化与随机故障过程，直至设备性能退化至不可接受状态Ak+d(d=2,3,…,n-k-d)。假设一旦发现设备处于最后一个可接受状态Ak+1，则立即进行预防性维修，使设备性能恢复到更高一级的状态，这类维修任务通常在维修场所由中继级和基地级共同参与完成。根据预防性维修效果的不同，系统性能恢复程度相异，如果为最小程度的维修，则认为设备性能恢复至上一退化状态Ak；如果是最大程度的维修(即完美预防性维修)，设备性能恢复至名义性能状态A1；否则，系统性能恢复至二者之间的中间状态。

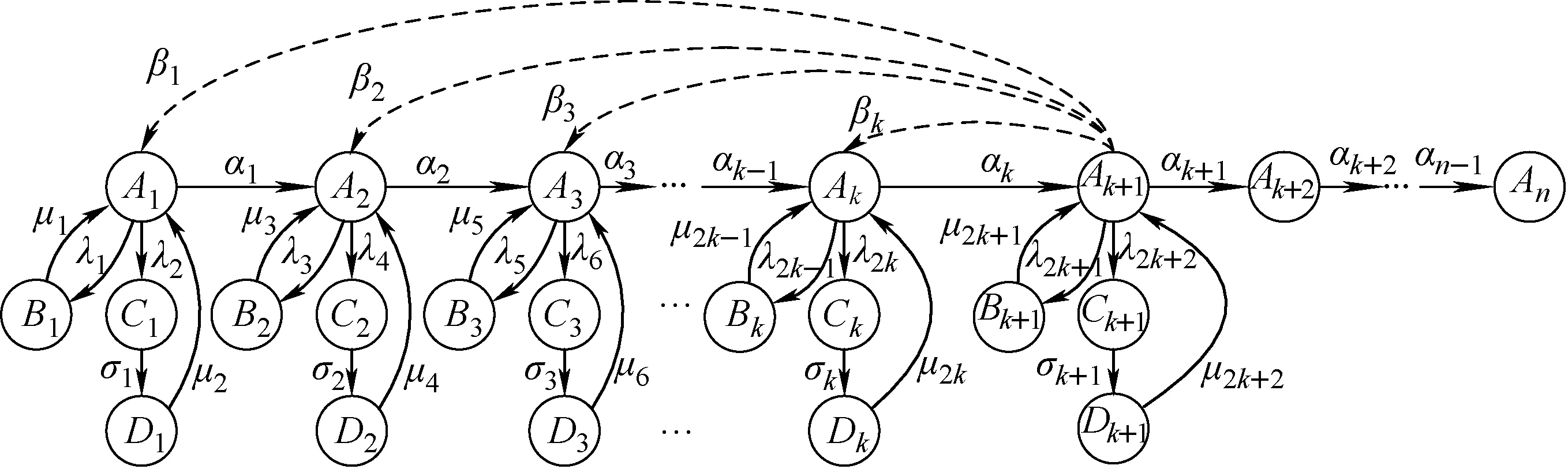
图1 设备状态转移图

根据图1，建立系统的状态转移方程：

(7)

初始条件为：

pA1(0)=1

pA2(0)=p(0)=…=pAn(0)=0

pX1(0)=pX2(0)=…=

pXk+1(0)=0X=B,C,D

并满足完备性：

其中：p为概率；t为时间。

通过求解式(7)，可得到设备在不同性能条件下的状态概率，进而代入系统的性能分布发生函数，得到系统在不同性能需求条件下的可用度。

2.3 故障率参数估计

一般情况下，船舶核动力装置缺少用于可用度计算的故障率数据，为此，需借鉴电站核动力设备的通用故障数据。由于电站核动力装置与船舶核动力装置在维修上的差异性，导致电站核动力设备故障率通用数据无法直接用于船舶核动力装置可用度计算。为此，定义可修率ν作为获取可修故障率与不可修故障率的统计参数，即发生可修故障次数与故障总次数的比值，可通过对历史故障数据进行极大似然估计得到。假设状态Ak(1≤k≤n-1)的随机故障率为λ(k)，可修率为νk，则有：

λ2k-1=λ(k)·νk

(8)

λ2k=λ(k)·(1-νk)

(9)

3 实例分析

图2所示的核动力装置由冷却剂泵(P)、蒸汽发生器(SG)和汽轮机(ST)等相关功能设备组成，其功能主要是为平台系统提供动力。考虑设备发生退化和随机故障，则可知该装置为多状态系统，通过设备性能之间的不同组合，系统具有多个性能输出。系统可用度分析的目标可归结为基于系统性能需求，在综合考虑设备性能退化和多级保障条件下定量评估装置特定时间区间(本文选取1 a)内的可用度。

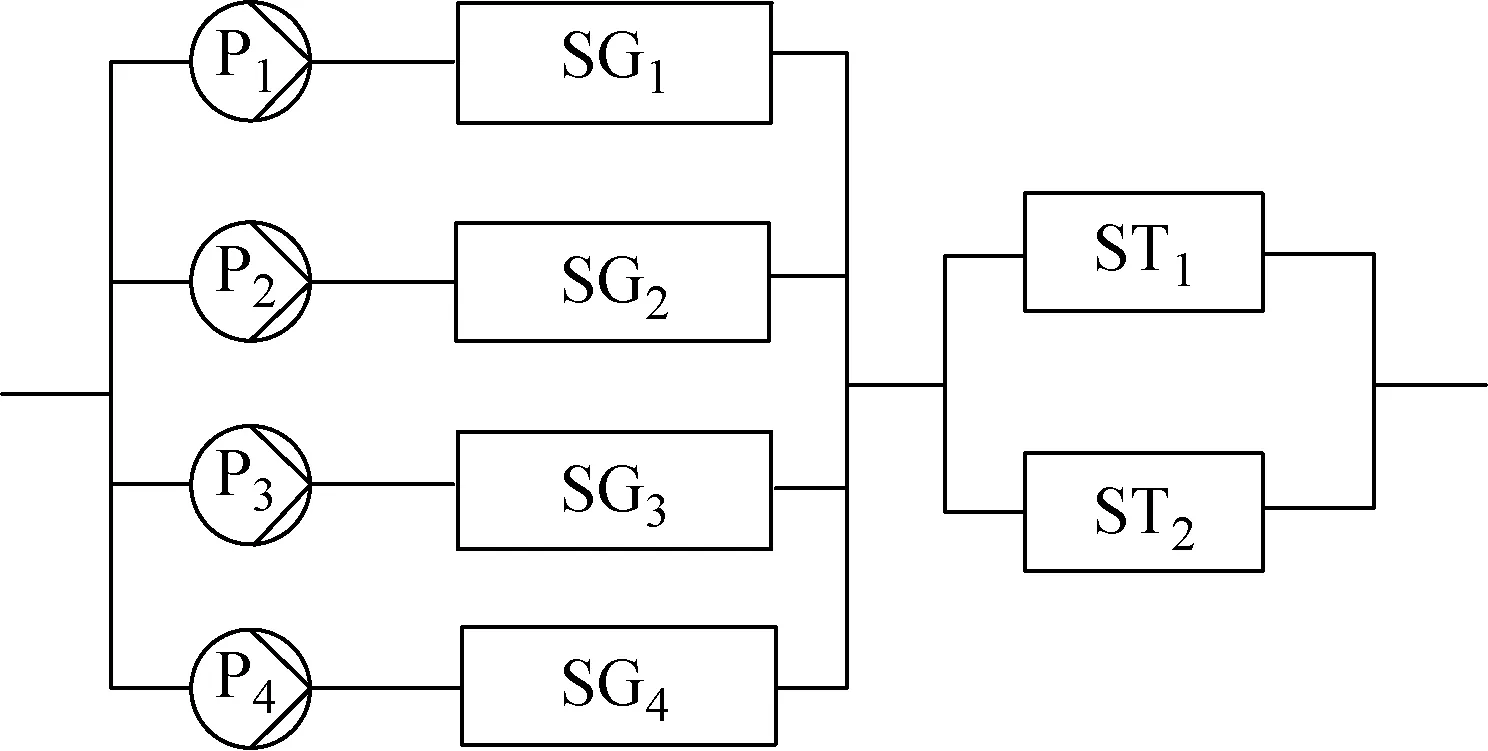
图2 核动力装置示意图

3.1 设备修理条件分析

对于冷却剂泵，在计划修理间隔期内(大于1 a)不考虑对其进行更换；对于汽轮机，在寿命周期内不能更换。对于二者而言，预防性维修只能部分恢复其性能状态，而不能使其恢复到名义性能状态，可认为对二者实施的预防性维修能覆盖除最大程度维修以外的任何程度。

对于蒸汽发生器，在计划修理间隔期内也不考虑对其进行更换，导致其性能降级的主要因素为因污垢造成传热系数恶化和因堵管造成传热面积减小，如果考虑前者能够通过预防性维修(如串水、冲洗等措施)得到改善，而堵管造成的传热面积减小却无法通过预防性维修加以解决。同时，考虑到蒸汽发生器传热管的裕量较大，而且传热管的破损率较低，因此，可假定其预防性维修为最小程度的维修，通过预防性维修能使其性能恢复至上一退化状态。

3.2 数据给定

根据以上分析，考虑冷却剂泵和汽轮机具有3个退化状态、1个完好状态和1个完全失效状态，即k=3、n=5；考虑蒸汽发生器具有2个退化状态、1个完好状态和1个完全失效状态，即k=2、n=4。系统组成设备的名义性能值(定义为满足系统额定需求的百分比[2]，系统存在性能输出的裕度)和系统分析时需要的各参数列于表1、2，其中失效数据参考文献[4]并结合工程改进现状加以确定，不考虑预防性维修时间，假设同一类型设备的各不同状态的故障可修率相同。

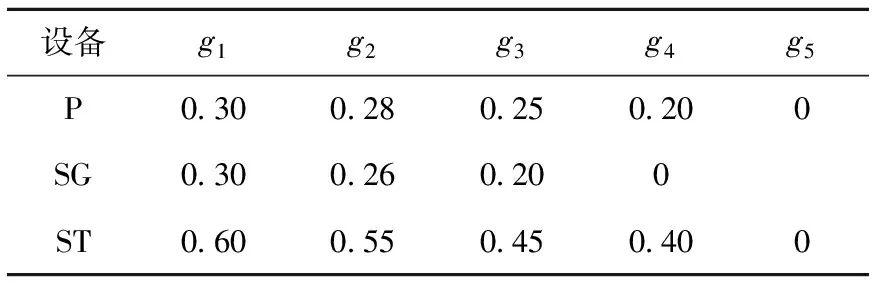
表1 设备性能值

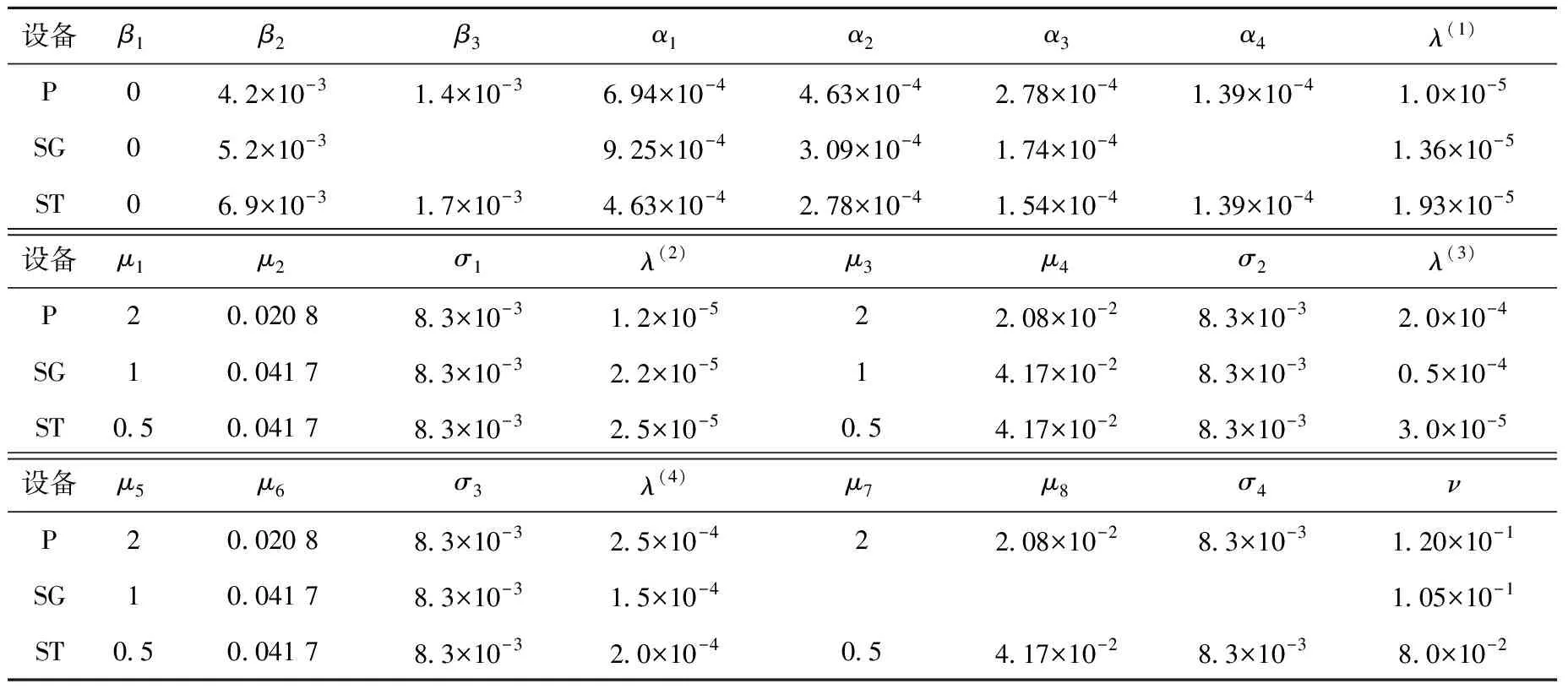
表2 设备参数表

3.3 定量计算

根据表2数据，首先采用式(8)、(9)获得设备的可修故障率与不可修故障率，进而采用式(7)计算系统各设备在各性能条件下的状态概率，然后根据式(1)得到各设备的发生函数，将其代入系统发生函数(式(2))，根据系统逻辑结构进行设备性能的最小值运算或求和运算以及对应状态概率的求积运算，确定出系统的性能发生函数表达式，最终根据式(6)确定出在满足需求性能w条件下的可用度结果。本文分别计算了w分别为0.3、0.5、0.75、1.0情况下是否考虑预防性维修的可用度，分析结果示于图3。图3中有标志的曲线代表不考虑预防性维修的分析结果。同时，为了分析维修条件对系统可用度的影响，假设设备故障的平均现场维修时间不变，分别令3类设备的可修率(可修率实际上表征了现场维修能力，如维修场所设置的完善程度、维修人员技能的高低、备件是否充足等)同时增加至原值的k(k=2、4、8)倍，分析了w为0.3条件下的系统可用度变化情况，分析结果示于图4。

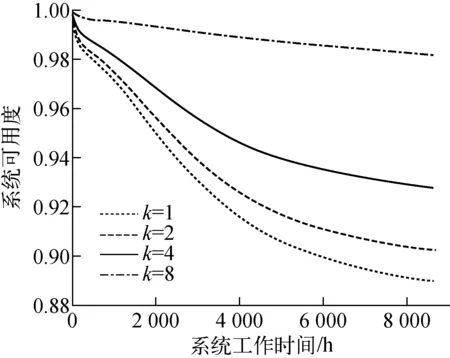
图4 w为0.3和提高k的情况下系统的可用度

3.4 结果分析

由图3的分析结果可知，考虑预防性维修后，系统可用度显著提高；系统需求性能值越大，其可用度越低，且随着工作时间的增加，其可用度之间的差距不断加大，在需求性能w为1.0时与0.3时相比，在工作1 a后，其可用度降低了近4倍。由图4可知，在需求性能一定的情况下，随着可修率的提高，系统可用度逐渐增大，这表明随着现场修理能力的提高，系统故障恢复能力得到了较大提升，降低了返回维修场所的时间延误对系统不可用时间的贡献。图4只是给出了在w为0.3情况下提高k的系统可用度，系统需求性能w取其他值情况下的系统可用度也可通过类似方法计算得到。

4 结论

本文研究了基于通用发生函数理论和Markov过程方法相结合的方法，对考虑性能退化和多级保障的核动力系统进行可用度分析。基于通用发生函数理论构建了系统的逻辑关系模型和设备性能状态组合模型，同时建立了在考虑性能退化和多级保障条件下的设备状态概率模型，从而计算了系统在不同性能需求条件下的可用度，并分析了不同修理条件对系统可用度的影响。本文所考虑的相关要素反映了核动力系统的实际使用和维修情况，研究方法能为核动力系统的保障条件分析提供模型支持，分析结果能为核动力系统的使用管理和维修决策提供理论指导和依据。

参考文献：

[1] SORO I, NOURELFATH M, KADI D. Performance evaluation of multi-state degraded system with minimal repairs and imperfect preventive maintenance[J]. Reliability Engineering and System Safety, 2010, 95: 65-69.

[2] LISNIANSKI A, LEVITIN G. Multi-state system reliability: Assessment, optimization and application[M]. Singapore: World Scientific Publishing Co. Pte. Ltd., 2003.

[3] LISNIANSKI A. Extended block diagram method for a multi-state system reliability assessment[J]. Reliability Engineering and System Safety, 2007, 50: 1 601-1 607.

[4] 阎凤文. 设备故障和人误数据分析[M]. 北京：原子能出版社，1988.