旋启式止回阀关阀水锤优化分析

韩文伟，韩伟实，郭 清，王 鑫，刘春雨

(哈尔滨工程大学 核科学与技术学院，黑龙江 哈尔滨 150001)

旋启式止回阀作为一种重要的单向阀，广泛应用于各类工程领域中，其基本原理是利用流动的流体对阀板做功，控制阀门开关状态，当流体正向流过阀门时推动阀板开启，当流体逆向通过时推动阀板与阀座闭合，达到阻止逆流的作用。在旋启式止回阀关闭过程中，由于流体运动状态突然变化，引起管道的弹性变形，此即为水锤现象。水锤对于输水系统威胁很大，几乎所有核电厂在整个运行期间都出现过水锤事故，有的水锤事故甚至会引起管道破裂与甩摆，拉断支撑并迫使核电厂停堆，如1985年11月在美国San Onofre发生的水锤事故就造成了上述严重后果。

国内外学者对水锤的形成理论、相关计算方法、影响因素以及缓解措施已进行了大量研究[1-5]。但在双泵并联给水系统切换过程中，对止回阀的水锤特性研究较少。本文拟以旋启式止回阀为研究对象，选取双泵并联给水系统作为研究背景，针对系统中的离心泵、止回阀、阻力件以及管道建立数学物理模型，通过编程计算分析止回阀阀板所受力矩以及阻尼扭簧力矩对关阀水锤的影响，为该类止回阀[6]的设计制造提供技术参考。

1 数学物理模型

在求解管道中的水锤问题时，通常将流动看作一维非恒定流动。一维非恒定流动的基本方程组包括连续性方程和运动方程。本文的水锤计算利用数值解法，数值解法主要有特征线法和有限差分法。目前水锤计算主要是采用特征线法。特征线法的原理是：将偏微分方程组转化为特殊的全微分方程，即特征方程，然后再转化为一阶有限差分方程，求其近似解[7-9]。

设阀门进出口与管道连接处分别为1、2号点，P1和P2分别为1号点和2号点的顺波(正向波)特征线与逆波(负向波)特征线的交点，在阀门前后有相同的流量，同时，对每一根管道，均可对其端点写出适用的相容性特征方程：

HP1=CP1-B1QP1

HP2=CP2+B2QP2

QP=QP1=QP2

(1)

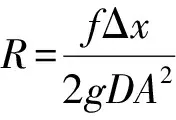
通常情况下，流过阀门孔口的压降ΔH=HP1-HP2，与泵流量Q0和压降ΔH0有如下关系：

(2)

式中，τ为阀门的无量纲开度，与阀板的开启角度θ相对应。

联立式(1)、(2)可得：

CP1>CP2时，

QP=-CV(B1+B2)+

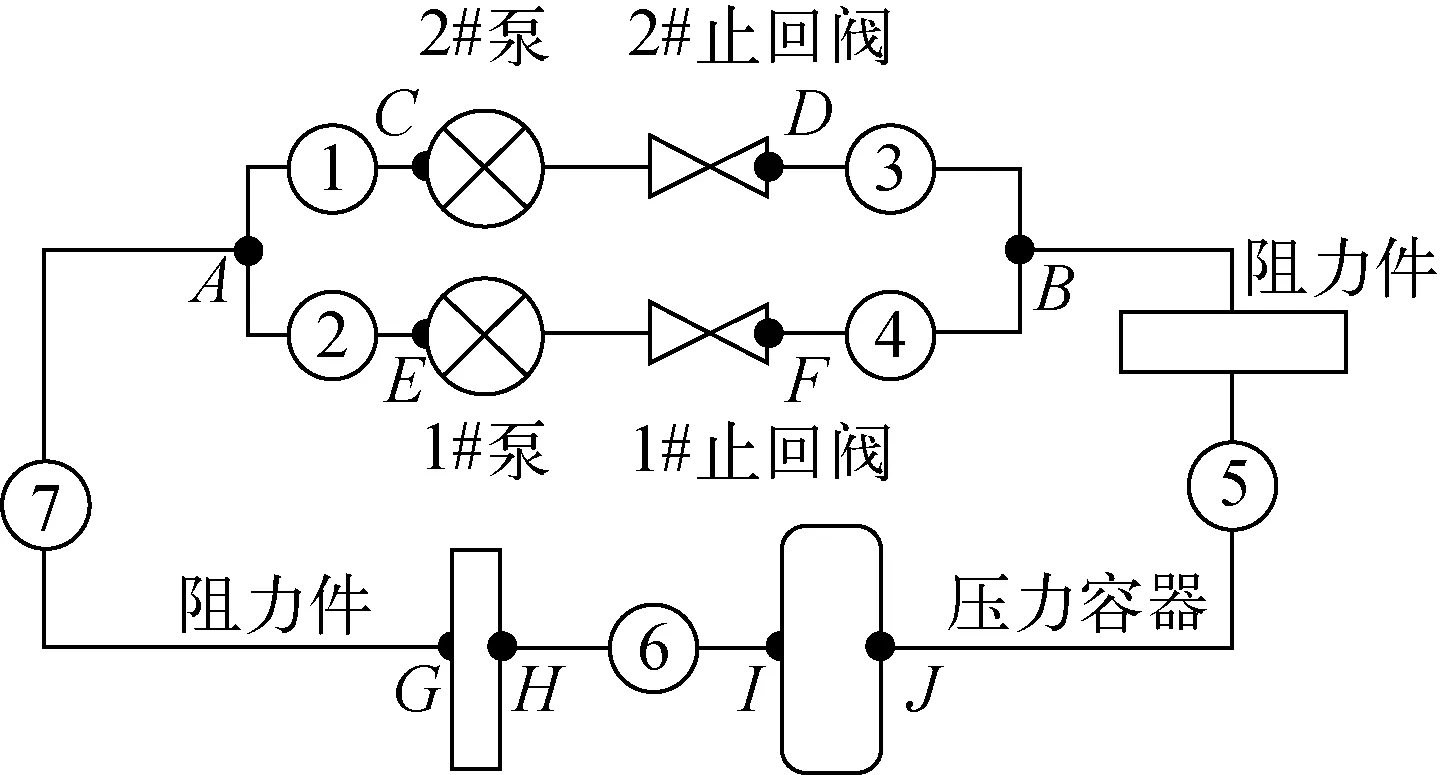
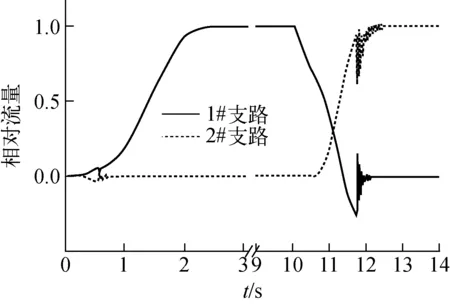
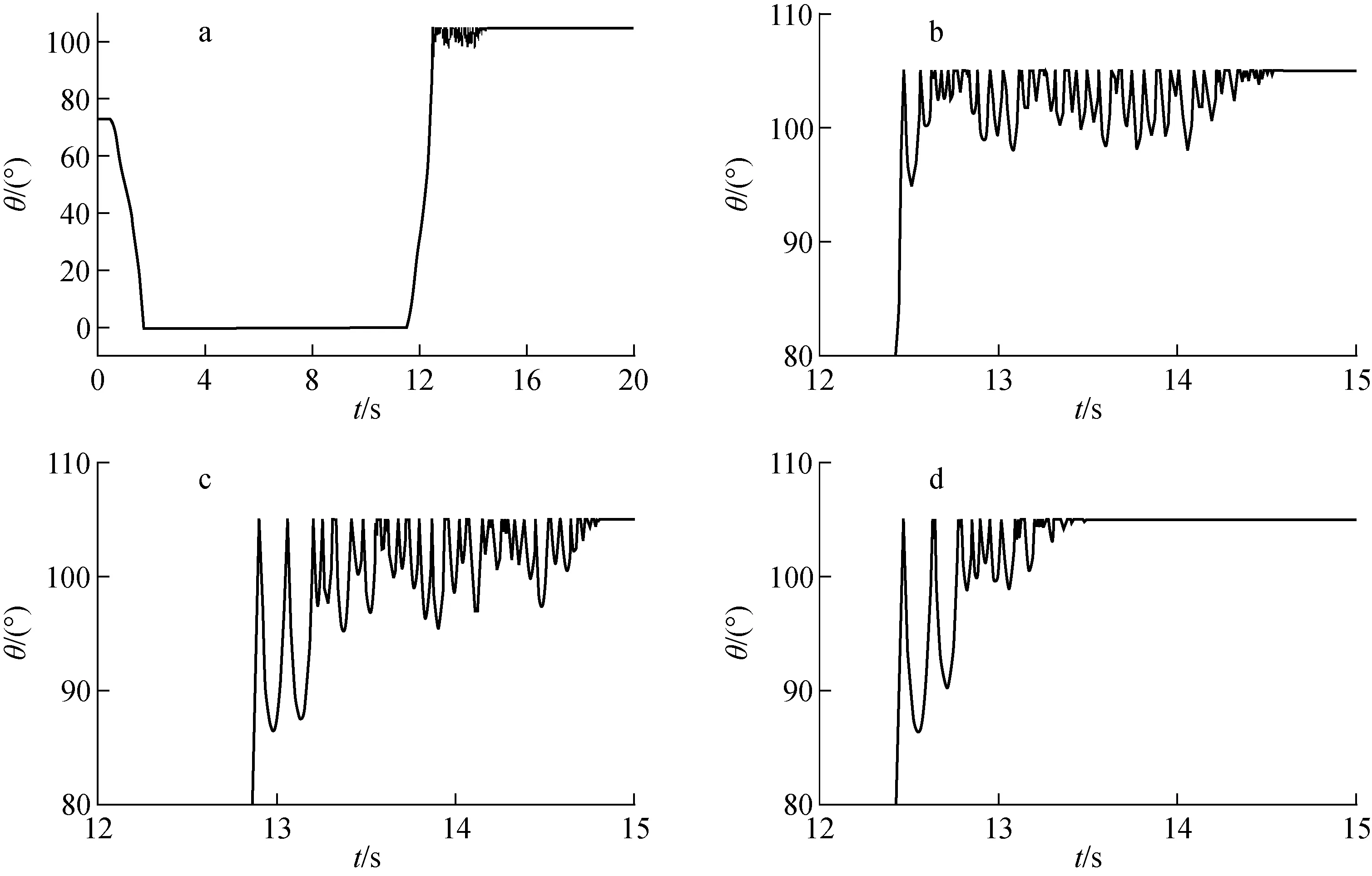
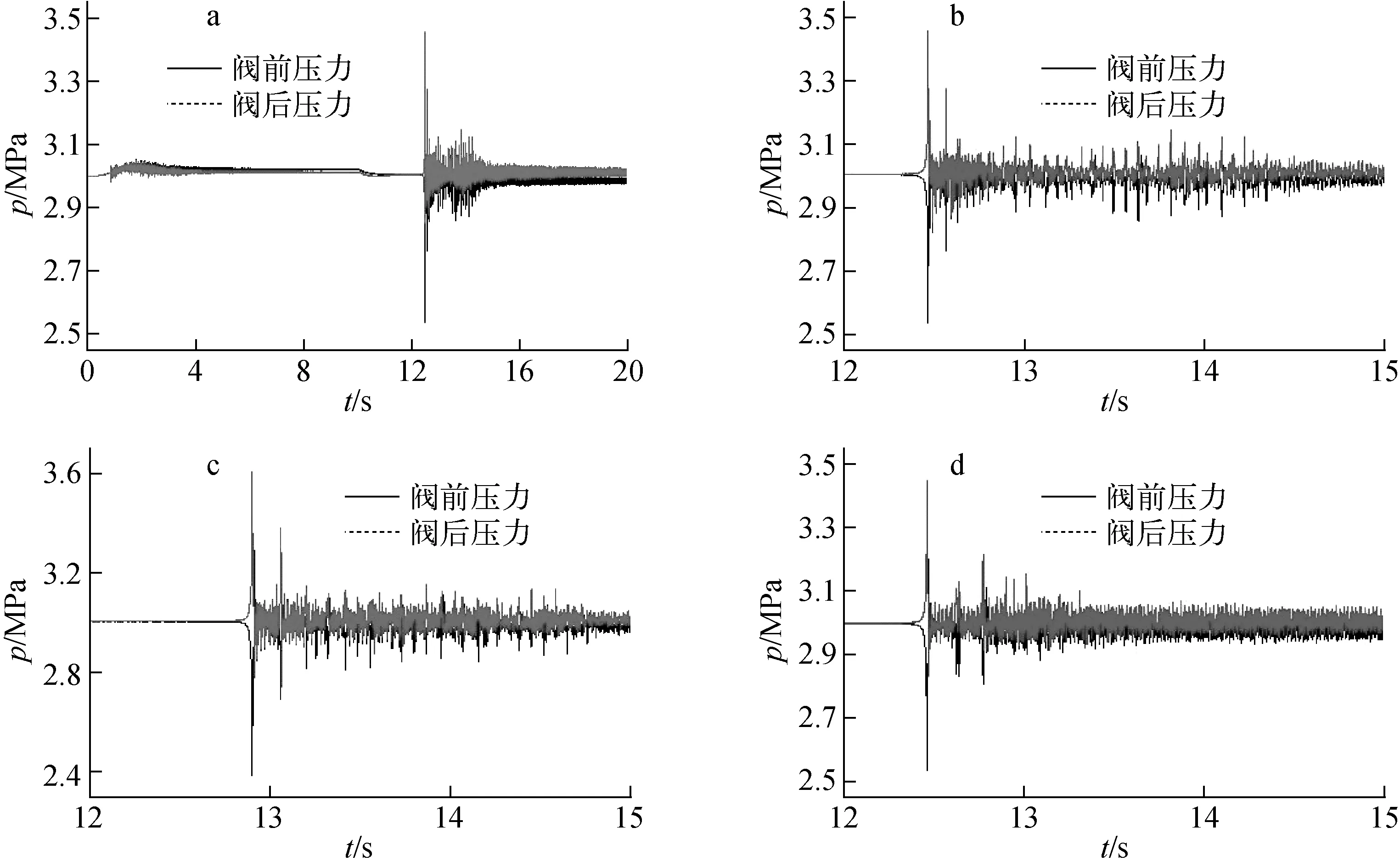
CP1

QP=CV(B1+B2)-

(3)

将流量代入式(1)可求得阀门两端的压头。θ可用式(4)表示：

MT+MB-MV-MF+MR

(4)

式中：I为阀板的转动惯量；MRF为阀门关闭瞬间撞击底座时的反作用力矩；MP为阀门前后静压差力矩；MH为水冲击力矩；MT为扭簧力矩；MB为阀板浮力力矩；MV为重力力矩；MF为摩擦力矩，指阀板转动时与转轴的摩擦力矩，一般可表示为阀板旋转角速度平方的函数；MR为阻力力矩，指流体流经阀板时流体与阀板表面间的摩擦力矩。各项力矩的求解模型如下。

1)MRF

阀板与阀座的碰撞力矩计算模型利用牛顿第二定律：

(5)

式中：ωm为撞击前角速度；ωn为撞击后角速度，程序中将其假设为碰撞前角速度的80%；Δt为碰撞作用时间，取1个时间步长，即Δt=0.385 2 s。

2)MP

因阀门前后压力不同产生作用于阀板的压差力矩，其表达式为：

MP=plSlL1-prSrL2

(6)

式中：pl和pr分别为阀板左、右两侧的压力；Sl和Sr分别为阀板左、右两侧的面积；L1和L2分别为压力作用点1和2到转轴的力臂。

3)MH

ρc(v-Lω1)

(7)

式中：CT为水冲力矩系数；D为阀盘直径；ρc为流体密度；ω1为阀盘转动角速度；L为质心到转轴的力臂；v为流体流动速度。CT一般由实验确定，程序中设定为阀门开启角度的函数，即CT=35sinθ。

4)MT

计算中将MT设置为零。

5)MB与MV之和

MB与MV的和由下式计算：

MG=MV+MB=[(ρV-ρc)/ρV]gmVLcosβ

(8)

式中：ρV为阀板材料密度；mV为阀板质量；β为按照通道中心轴起算的关闭角度。

6)MF

MF=CKω2

(9)

式中：CK为阀板与转动轴间的阻力系数；ω为阀板转动角速度。

7)MR

MR=Kρv′2SL

(10)

式中:K为阀板和流体间的阻力系数；v′为阀板运动速度；S为阀板面积。

2 边界条件

实际应用中为保证连续供水、提高给水系统的稳定性和可靠性，通常设置两台相同的离心泵，一台运行，另一台备用。在运行泵发生故障停机、不停止供水检修某一台给水泵以及均衡两台给水泵寿命等条件下，需进行给水泵切换，本试验中设计双泵并联给水系统，为防止支路倒流造成给水泵倒转，在每个支路给水泵下游均安装一个止回阀。试验装置结构如图1所示。

图1 试验装置结构示意图

计算中采用调整各段管长的方法将整个系统管道分为7段，每段的参数列于表1。最终选定时间步长Δt=0.385 2 s，取0.5 m为最小空间步长。管道内径为150 mm，管材为0Cr18Ni10Ti，设计温度为60 ℃，设计压力为8 MPa。A、B两点间1#泵支路长度L1=6.45 m，2#泵支路长度L2=5.32 m，其余管线长度L3=17.56 m。

阀门形式示意图如图2所示。取阀板与阀门流道水平线平行时的开启角度为0°，阀板与流道水平线垂直时的开启角度为90°。阀板在自然状态下的开启角度为73°，阀门关闭时刻的开启角度为105°。计算时仅考虑泵、阀及压力壳模拟容器，试验段其余附件简化为一个集总阻力件，其∑ξ=8.33，ξ为阻力系数。

表1 系统网格划分

图2 止回阀结构示意图

3 计算结果分析

针对双泵并联给水系统建立数学物理模型，利用特征线法求解方程，对1#泵向2#泵的切换过程进行数值模拟。具体切换过程为：t=0 s时刻，1#泵启动；1.3 s内达到额定转速；t=10 s时刻，1#泵停泵，2#泵启动。

图3为两台并联的离心泵切换过程中两条支路流量的变化趋势，图4a和图5a显示了1#和2#止回阀开启角度的变化曲线。可看出：当1#泵启动后，1#支路的流量逐渐增大，在第3.5 s时流量基本趋于稳定。1#泵的启动会导致2#支路存在很小的反转流量。在1#泵启动过程中，1#阀门迅速达到完全开启状态，其阀板角度为0°，2#阀门阀板在水冲力矩的作用下迅速达到关闭状态，其阀板角度为105°，并产生剧烈的水锤现象，2#阀门的阀板与阀座产生数十次剧烈碰撞(图5b)，从而引起2#泵阀前后流量和压力的波动，2#泵阀前后压力波动幅度达到约0.4 MPa。在第10 s 时刻，1#泵停闭，1#支路流量迅速衰减，同时2#泵启动，2#支路流量逐渐增大，2#泵的启动会导致1#阀的阀板数十次猛烈撞击阀座(图4b)，从而引起泵阀前后流量和压力的波动(图3和图6a)，泵阀前后压力波动幅度达1.0 MPa左右。由于压力的波动出现在水锤过程中，导致1#泵和2#泵的流量也出现了一定的波动。

图3 1#和2#支路的流量变化

a——原始方案；b——a的局部放大；c——优化方案1；d——优化方案2

为有效缓解水锤作用的危害，对作用在阀板上的力矩以及阻尼扭簧力矩进行敏感性分析，本文提出两个优化方案：

方案1：改变作用在阀板上的浮力力矩MB。通过选材改变阀板的密度，实现阀板所受力矩的改变，经大量计算分析，确定优化计算的密度为2 000 kg/m3。

方案2：增加阻尼扭簧力矩MT。根据阀板运动特性，当阀板关闭角度大于90°时，给阀板施加一负的(阻碍阀门关闭的方向)扭簧力矩，以延迟它的关闭，减小阀门关闭时的水流速度，进而减弱并消除水锤导致的阀板与阀座碰撞。具体方案为：当阀板的关闭角度大于90°时，添加一个阻力矩，使得MT=500AH(A为阀板面积，H为压力作用中心到转轴的距离)。

对两种优化方案分别进行计算，并比较双泵切换过程中1#和2#止回阀阀板的开启角度以及阀门动作前后压力的变化情况，结果示于图4～7。

在0～3.5 s内，1#泵开启，1#止回阀由自然状态变为开启，阀板角度由73°变为0°，2#止回阀由自然状态变为关闭状态，阀板角度变为105°。通过计算发现，2#止回阀在关闭过程中，角度多次达到105°并出现反弹，说明阀板与阀座撞击后又多次出现撞击波动，阀板不能一次关严，这将进一步引起系统流量和压力的波动，如图5a、b及图7a、b所示。两种优化方案的计算结果如图5c、d以及图7c、d所示。通过计算发现，两种优化方案中2#止回阀关闭时阀板同样与阀座多次撞击，但撞击的次数明显减少，阀板震动幅度也同样减小，且阀板能较快达到105°的关闭状态，波动时间明显缩短。由于阀板撞击减少，2#止回阀前后压力震荡也有所缓解，压力波动幅度减小，同时震荡时间缩短。

在10～15 s内，1#泵关闭的同时切换2#泵开启，1#止回阀由开启变为关闭状态，阀板角度由0°变为105°，2#止回阀由关闭状态变为开启状态，阀板角度变为0°。在1#止回阀关闭过程中，角度多次达到105°并出现反弹，与2#止回阀关闭过程相似，1#止回阀阀板与阀座撞击后又多次出现撞击波动，且引起系统流量和压力的波动，如图4a、b及图6a、b所示。两种优化方案的计算结果如图4c、d及图6c、d所示。两种优化方案中，方案2的效果较好，1#止回阀关闭时阀板与阀座的撞击次数明显减少，且阀板能较快达到105°的关闭状态，波动时间明显缩短。由于阀板撞击减少，系统压力震荡也有所缓解。

a——原始方案；b——a的局部放大；c——优化方案1；d——优化方案2

a——原始方案；b——a的局部放大；c——优化方案1；d——优化方案2

a——原始方案；b——a的局部放大；c——优化方案1；d——优化方案2

4 结论

建立了双泵并联给水系统的数学物理模型，利用特征线法计算了水锤特征方程。计算结果显示，在止回阀关闭过程中作用在阀板上的力矩对水锤的作用效果有一定影响，可通过选择合适的止回阀阀板材料优化阀板受到的力矩，进而降低水锤危害。另外，对阀板施加一阻碍阀门关闭的扭簧阻尼力矩，可减小阀门关闭时的水流速度，有效缓解水锤危害。

参考文献：

[1] 古智生. 泵站拍门撞击力的简化计算方法及其应用[J].中国农村水利水电，2000(8): 45-47.

GU Zhisheng. Pumping-door impact force simplified calculation method and its application[J]. China Rural Water and Hydropower, 2000(8): 45-47(in Chinese).

[2] KOCHUPILLAI J, GANESAN N, PADMANABHAN C. A new finite element formulation based on the velocity of flow for water hammer problems[J]. International Journal of Pressure Vessels and Piping, 2005, 82(1): 1-14.

[3] TUOMAS G. Effective use of water in a system for water driven hammer drilling[J]. Tunnelling and Underground Space Technology, 2004, 19: 69-78.

[4] BERGANT A, SIMPSON A R, TIJSSELING A S. Water hammer with column separation: A historical review[J]. Journal of Fluids and Structures, 2006, 22: 135-171.

[5] WOLFGANG S. Minimising the risk of water hammer and other problem at the beginning of stagnation of solar thermal plants: A theoretical approach[J]. Solar Energy, 2000, 69: 187-196.

[6] 孙育哲,雷徐. 新型旋启式止回阀在技术供水系统中的应用[J]. 浙江水利水电专科学校学报,2012,23(2):12-14.

SUN Yuzhe, LEI Xu. New type swing check valves in technological water supply system[J]. Zhejiang Water Conservancy and Hydropower College, 2012, 23(2): 12-14(in Chinese).

[7] 李树勋,侯英哲,李连翠,等. 液流旋启式止回阀关闭动态特性数值模拟[J]. 排灌机械工程学报,2013,31(4):335-339,344.

LI Shuxun, HOU Yingzhe, LI Liancui, et al. Numerical simulation on dynamic characteristic of closing process of flow swing check valve[J]. Drainage and Irrigation Machinery, 2013, 31(4): 335-339, 344(in Chinese).

[8] 韩伟实,王鑫,幸奠川,等. 双泵给水系统水锤敏感度分析[J]. 中国农村水利水电,2012(5):136-139.

HAN Weishi, WANG Xin, XING Dianchuan, et al. An analysis of water hammer sensitivity in double-pump water supply systems[J]. China Rural Water and Hydropower, 2012(5): 136-139(in Chinese).

[9] 巴鹏,皱长星,陈卫丹. 截止阀启闭时流动特征的动态数值模拟[J]. 振动与冲击,2010,29(10):157-l61.

BA Peng, ZOU Changxing, CHEN Weidan. Dynamic numerical simulation of flow features during stop-valve’s opening or closing[J]. Journal of Vibration and Shock, 2010, 29(10): 157-161(in Chinese).