压水堆蒸汽发生器一、二次侧稳态流场耦合分析

丛腾龙，田文喜，秋穗正，苏光辉，谢永诚，姚彦贵

(1.西安交通大学 能源与动力工程学院，陕西 西安 710049；2.上海核工程研究设计院，上海 200233)

蒸汽发生器(SG)作为压水堆的关键设备同时承担着一、二回路侧换热以及一回路压力边界的作用，在反应堆运行过程中需保持传热管的完整性；然而在反应堆运行期间，传热管易出现震动、疲劳及由此带来的磨损甚至破裂。传热管的失效主要是由于管束震动引起的磨损、管束热应力损坏及事故工况时管束最高温度超限造成的，对以上因素进行分析需以SG二次侧的速度场、温度场作为输入参数。由于SG结构复杂、体积庞大，对SG二次侧流场进行实验和精细网格的CFD计算难以实现，因此本文采用多孔介质模型对SG二次侧流场进行数值分析。

最早将多孔介质模型应用于换热器的是英国学者Patankar等[1]，他们于20世纪70年代就采用此模型对换热器壳侧进行了数值模拟。之后，Sha等[2]又在文献[1]的基础上模拟了SG和反应堆堆芯中冷却剂的流动，Prithiviraj等[3-4]模拟了三维换热器中的流动。Ferng等[5-7]采用CFX软件多孔介质模型对SG管束区的二次侧流场进行了分析。

目前虽已有一些针对SG二次侧流体热工水力特性的CFD研究，但这些研究仍有待改进。在Ferng等[5-12]的研究中，存在如下问题：1) 进出口边界设置不合理；2) 两相流计算关系式过于粗糙；3) 采用不正确的阻力和湍流计算模型；4) 计算忽略下降段、支承板和汽水分离器，这一系列简化或不合理假设，导致计算结果和实际运行情况差别很大，计算结果在工程应用上不具备参考价值。基于以上分析，本文采用多孔介质模型，对压水堆SG二次侧流场进行数值模拟，同时耦合一、二次侧一维换热。在模拟中综合考虑管束、下降段、汽水分离器、支承板的阻力影响。

1 数学物理模型

常用的两相流计算模型包含均匀流模型、漂移流模型和两流体模型。均匀流模型将两相流体等效为单相流体，不能描述两相间的滑移速度等。两流体模型可准确描述两相间的热力和水力学不平衡性，但由于管束外流动的相间作用力及相间传热等模型目前尚不完备，采用该模型需引入较多假设，导致两流体模型的计算精度不能保证。漂移流模型将两相流体视为混合相，但在相间引入漂移速度，考虑相间的水力学不平衡性，该模型虽从理论上相对于两流体模型精度较差，但由于该模型需引入的假设条件较少，计算精度可满足SG内多孔介质模拟的要求[13]。基于上述考虑本文采用漂移流模型。多孔介质内的漂移流模型控制方程如下。

质量守恒方程：

β·(βρmvm)=0

(1)

β·(βρmvmvm)=-β

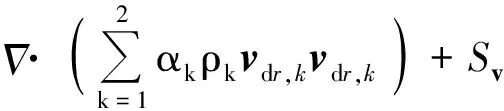
(2)

能量守恒方程：

β·

(3)

空泡份额方程：

β·(βαgρgvm)=

(4)

式中：β为孔隙率，即网格中流体体积与网格总体积之比；ρ为密度，其中下标m和g分别代表混合物和气相；vm为混合物速度；μm,eff为混合物有效黏度，等于混合物分子黏度和湍流黏度之和；αk为第k相体积份额；p为压力；S为附加源项，下标v、E、m分别代表动量、能量、质量；F为除SG内构件引入的附加力外的所有混合物所受体积力，如重力；keff为有效热传导系数；vdr,k为第k相的漂移速度。

动量、能量、空泡份额方程中的源项定义如下。动量方程中的源项表示由于控制体内SG构件的存在导致的附加阻力，包括下降段阻力、管束阻力、汽水分离器阻力、支承板阻力，其中，前3个阻力均为分布阻力，以分布阻力的形式添加到控制体网格，支承板阻力为局部阻力，以多孔阶跃模型的方式添加到支承板所在位置的网格界面上。对顺流和横掠阻力分别采用管束外顺流[14]和横掠[15]阻力经验关系式计算。支承板、下降段和汽水分离器的阻力，根据SG设计参数给定[13]。

能量方程的源项，即一次侧向二次侧释热，被简化为一维分布计算。将管束等效为1根传热管，二次侧流场也沿管束划分一维控制体，对于直管段冷、热侧分别划分11个控制体，弯管区域冷、热侧各划分1个控制体，共计24个控制体。U型管内为单相液体对流，采用Dittus-Boelter公式[16]计算；管外换热包括单相对流换热、过冷沸腾换热及饱和沸腾换热，对于单相对流换热，由于目前的经验关系式多为管外顺流和横掠关系式，无倾斜冲刷管束的换热关系式，因此将流速分解为顺流和横掠流速，分别计算顺流换热系数[17-18]和横掠换热系数[19]，将这两者的加权和[13]作为实际的斜掠换热系数。在计算中，给定一次侧入口的质量流速和温度，即可计算一、二次侧间的换热。

空泡份额方程中的源项表示气相质量源项，其值等于蒸发率与冷凝率之差，对于稳态计算忽略SG内的非稳态冷凝现象，气相质量源项等于液相蒸发率。

对于湍流模型，已公开发表的模型多针对纯流体区域的精细网格提出[20]，对于多孔介质内的湍流模型，研究者在多孔介质粗网格内对已有湍流模型(如k-ε)进行积分得到适用于多孔介质的湍流模型[9-11]，但这些模型仅用于单相流动，并无针对两相流动的湍流模型。本文采用文献[21-22]提出的针对管束间两相流动的零方程湍流模型计算湍流黏性及有效黏性，该模型已在ATHOS程序中验证[13,23]。

以上模型构成完备的控制方程组，将这些方程在ANSYS FLUENT求解器中求解可获得三维流场解，本文所采用的求解方法为COUPLE算法。

动员各方面力量搞好村庄环境宣传，把全体村民发动起来，让他们都真正理解支持，是每个村民都能做到爱村、护村，并行动起来，投入到美丽村庄建设上来，形成合力势头和建设发展力。

2 网格划分及边界条件

本文所选取的计算区域从下降段入口向下到围板缺口，然后折流进入管束区，最终进入汽水分离器，计算区域示意图如图1a所示。为简化网格划分，采用方形通道代替圆筒形的汽水分离器筒体，保持筒体流通面积和中心位置不变。所有网格均为六面体网格，在支承板位置添加内部边界面作为多孔阶跃边界。网格划分如图1b所示，网格质量大于0.5。

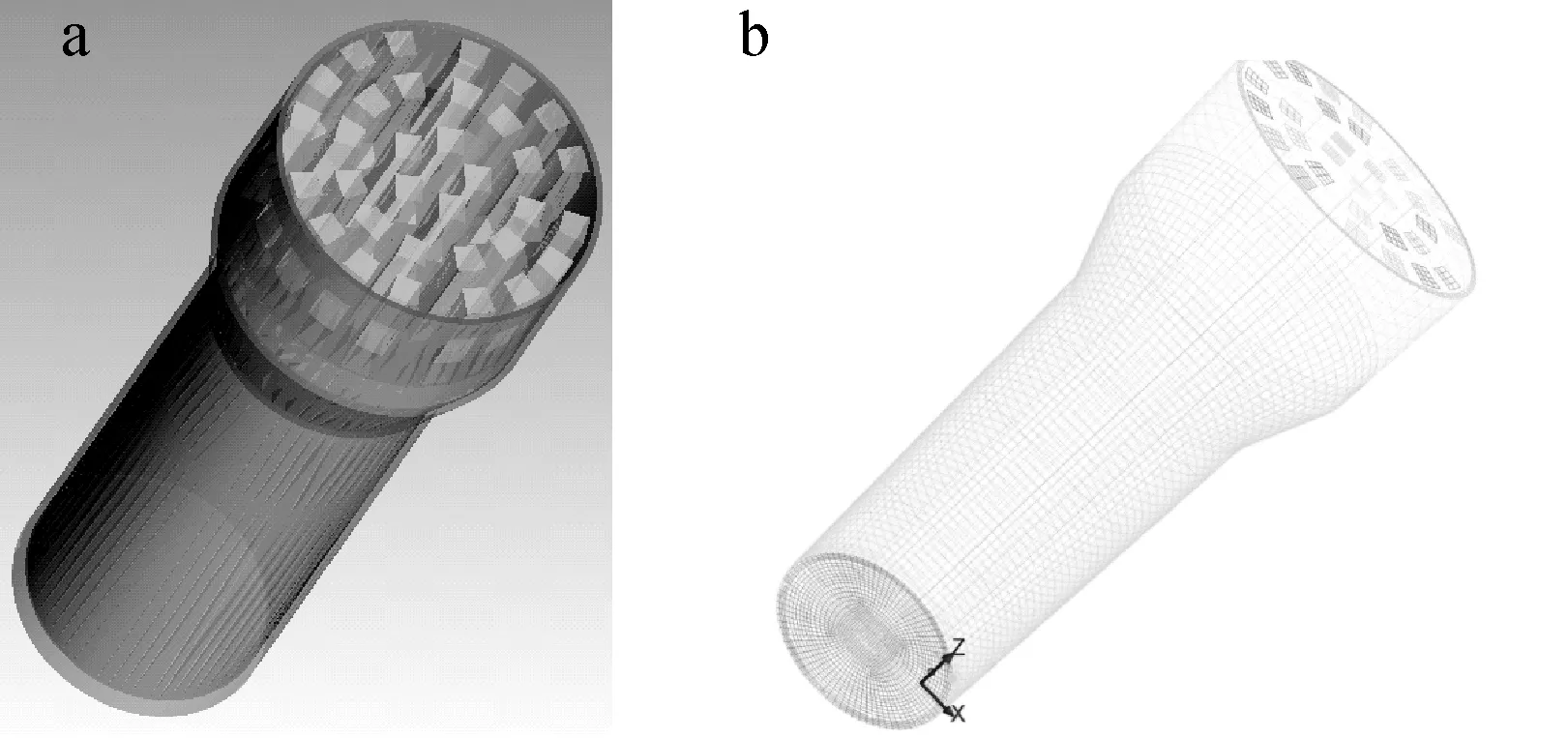
图1 计算区域(a)及网格划分(b)示意图

网格进口边界设置为速度进口，出口边界设置为压力出口，考虑到多孔介质网格尺寸较大，壁面无滑移边界不适用，因此本文采用滑移壁面边界条件，将壁面摩擦阻力分布添加到壁面网格内。入口温度采用疏水和新给水的焓计算，出口压力设置为SG顶部腔室压力。

3 结果分析

采用FLUENT计算二次侧流场、同时耦合一次侧一维流场，得到二次侧三维流场分布、一次侧一维流场分布及一、二次侧间耦合换热系数分布。FLUENT计算值与设计值对比列于表1。

表1 FLUENT计算值与设计值的对比

3.1 一、二次侧温度分析

图2为SG二次侧流体温度分布，图2a中右侧(x>0)为热侧、左侧为冷侧。由图2a可看出，热侧流体在进入管束区后很快达到饱和温度，而冷侧流体缓慢达到饱和，冷侧流体流过SG内1/2高度时才完全达到饱和，达到饱和后流体温度保持不变。由图2b的横切面温度分布可看出，由于流动和几何的对称性，流体温度关于y=0平面对称。

图3为竖直线和水平线上的温度分布。由图3可看出，随着轴向位置的升高冷却剂温度逐渐升高，且热侧(30、31曲线)流体升高速度远较冷侧(18曲线)的大，冷侧流体在高度上升到7 m时才达到饱和，而热侧流体在管板附近即达到饱和。由对称截面上水平线上的温度分布可看出，当位于较低位置(z=0.2,1.0,3.0 m)时流体温度在径向分布很不均匀，径向中心位置流体温度较高，靠近外围区域流体温度较低，随着流动的进行径向外围区域流体温度升高，且热侧温度高于冷侧温度。

图4为流体及传热管温度的一维分布。由图4可看出，一次侧流体温度随流动的进行逐渐降低，且随沿管束流程的增加流体温度降低速度减缓。热侧的二次侧流体温度沿轴向高度的增大很快达到饱和温度，之后维持在饱和温度544.7 K，冷侧流体温度沿轴向高度的增大缓慢达到饱和温度。传热管温度沿管束方向先增大后减小、之后又缓慢增大。这是由于在二次侧流体温度低于饱和温度时，平均后的管外换热属于单相对流换热，换热系数较小；当流体温度达到饱和后，沸腾换热系数远大于单相对流换热系数。一、二次侧的换热系数如图5所示，由于物性的变化，一次侧单相对流换热系数逐渐降低。二次侧换热系数在进入沸腾换热区域后迅速增大，在沸腾区域换热系数缓慢降低，直到再次进入单相对流区域又迅速降低。由于一、二次侧换热系数的突变，导致传热管内、外壁面温度在单相对流区域升高。

a——对称截面；b——不同高度水平截面

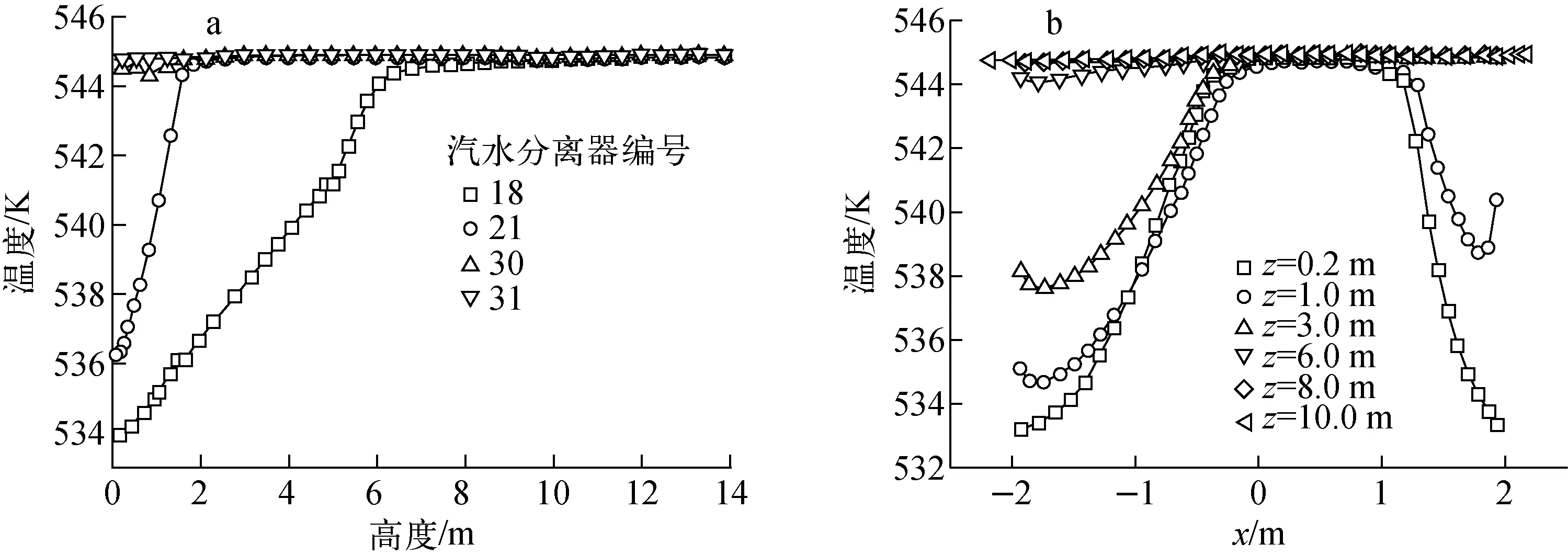
a——沿汽水分离器中心竖直线；b——沿对称截面上水平线

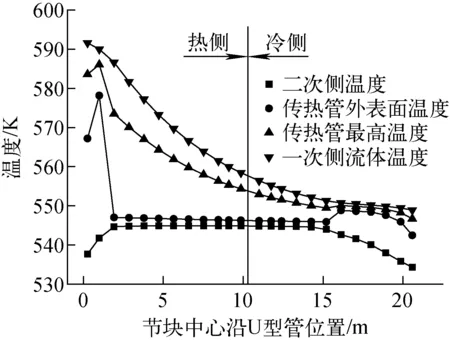
图4 流体及传热管温度的一维分布

3.2 二次侧流动含气率分析

SG二次侧流体的流动含气率分布如图6所示。由图6可看出，在管束进口区域冷、热侧含气率差别较大，热侧流动含气率小于0.01的区域很小；而冷侧该区域占较大面积。随着流体沿管束上升，流体不断蒸发，气泡在横向扩散，冷、热侧含气率逐渐均衡，且热侧靠近中心处含气率逐渐变为最大。

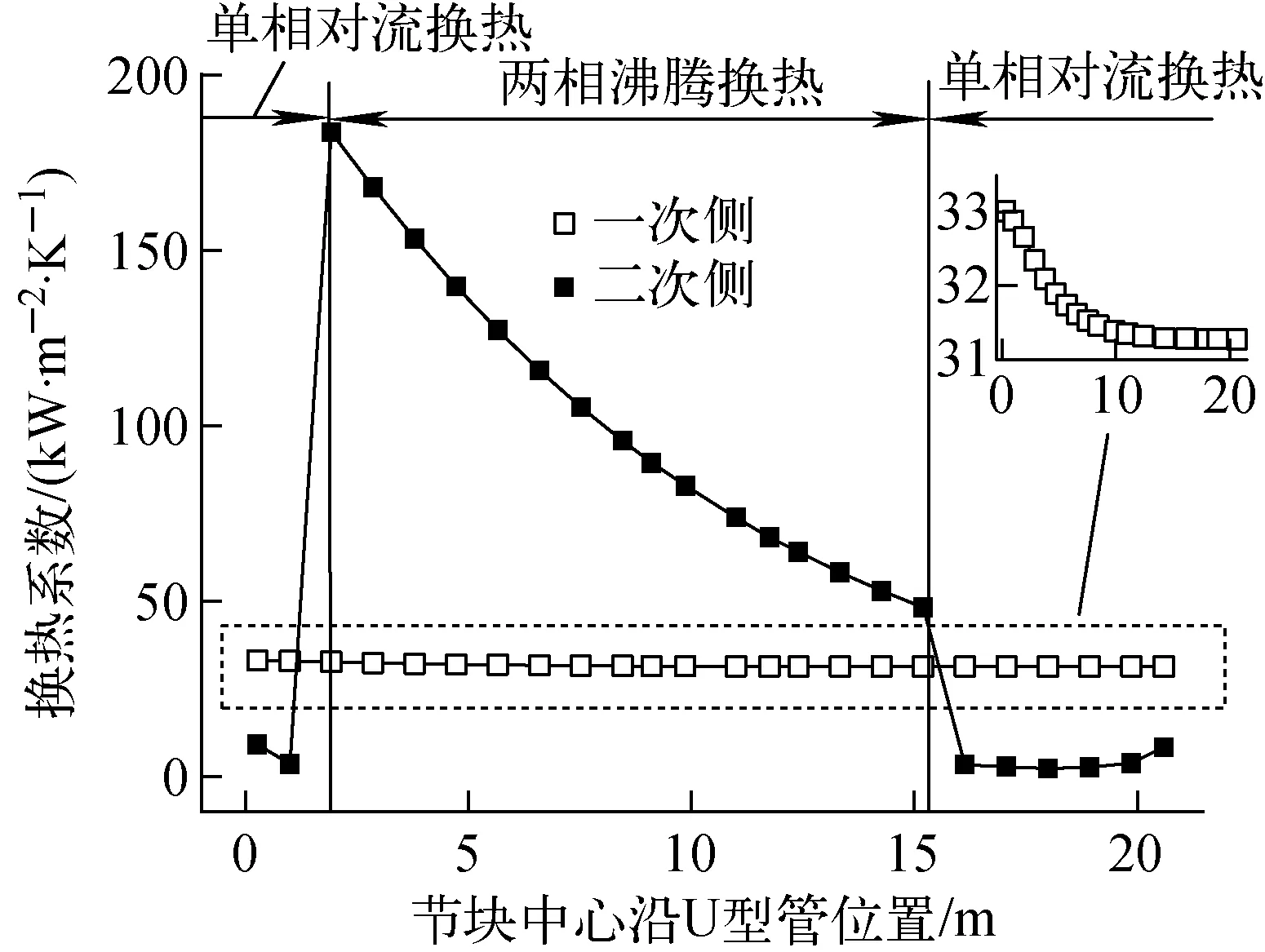
图5 换热系数分布

图7为竖直线和水平线上的流动含气率分布。流动含气率随轴向位置的增大而增大，热侧含气率远大于冷侧的。同一高度上含气率的最大值出现在热侧靠中心区域，含气率的峰值随轴向高度的增大逐渐向中心线移动。

a——对称截面；b——不同高度水平截面

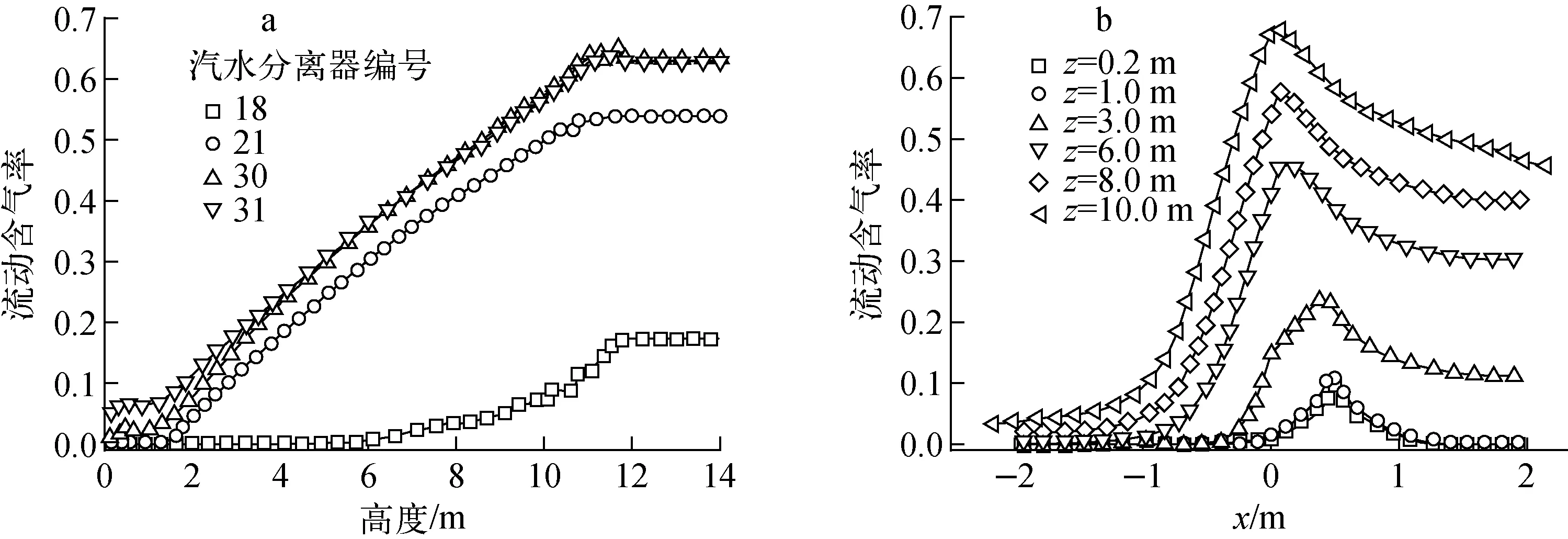
a——沿汽水分离器中心竖直线；b——沿对称截面上水平线

图8为汽水分离器内流动含气率的分布。由图8可看出，对于热侧最内层汽水分离器，其含气率很高，达0.62，而对于冷侧外围的汽水分离器，含气率仅0.05，不同的汽水分离器内混合物流动情况相差很大。

图8 汽水分离器内流动含气率分布

3.3 二次侧压力分析

图9 对称截面压力分布

图9为对称截面上的压力分布，压力选取出口截面为参考面，该截面压力设为0 Pa，图中标注压力为相对于参考压力的相对压力。由图9可看出，由重位压降、下降腔室壁面摩擦压降和加速压降的共同作用，下降段的压力沿下降段向下逐渐增大；由于流体转向，流体在围板缺口区域压力陡增，之后进入管束区域，流体压力随高度方向逐渐减小。由图还可看出，同一高度截面上热侧压力总体稍大于冷侧压力。图10为压力沿竖直线上的分布，压力沿高度方向出现明显的阶跃变化，这是由于支承板的存在，引入局部阻力，导致流体经过支承板时，压力突降；支承板导致压降随轴线高度的增大而增大，这是由于随高度的增加，两相流体含气率增大，两相摩擦压降倍增因子增大，从而在相同的阻力系数下，支承板位置越高，引入的压降越大。

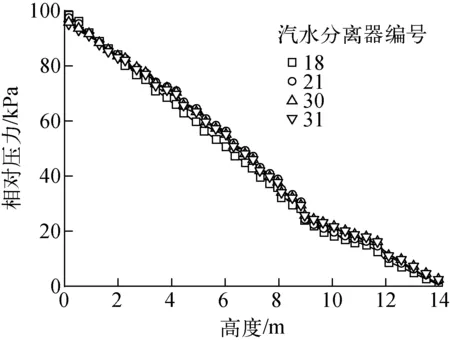
图10 压力沿汽水分离器中心线的分布

3.4 二次侧速度分析

图11为对称截面速度矢量图。由图11可看出，热侧流体速度明显大于冷侧的，最大速度约8 m/s。除围板缺口折流部分和弯管区域，流体基本沿管束方向流动，横流较小。管束区域流体速度矢量图如图12所示。

图11 对称截面速度矢量图

竖直线和水平线上的速度分布如图13所示。由图13可看出，对于热侧流体，由于蒸发的作用，在管束区流体速度沿高度方向迅速上升；对于冷侧流体，高度小于5 m时流体速度有轻微下降趋势，这是由于冷侧单相流体在流动过程中逐渐均匀化，5 m后由于蒸发的作用，流体速度开始上升。当流体流出管束区时，由于流通面积的增大，流体流速迅速降低，之后流入汽水分离器，由于流通面积减小，流体速度增大。由于冷、热侧加热不均匀，流速在径向上的分布也极不均匀。对于缺口高度的流体(z=0.2 m)，由于流体的折流，在外围(即围板缺口区域)流体流速较高，中心流速较低；随高度的增大，热侧流体开始蒸发，流速逐渐升高，流速峰值出现在中心偏热侧区域。

图12 对称截面弯管部分速度矢量图

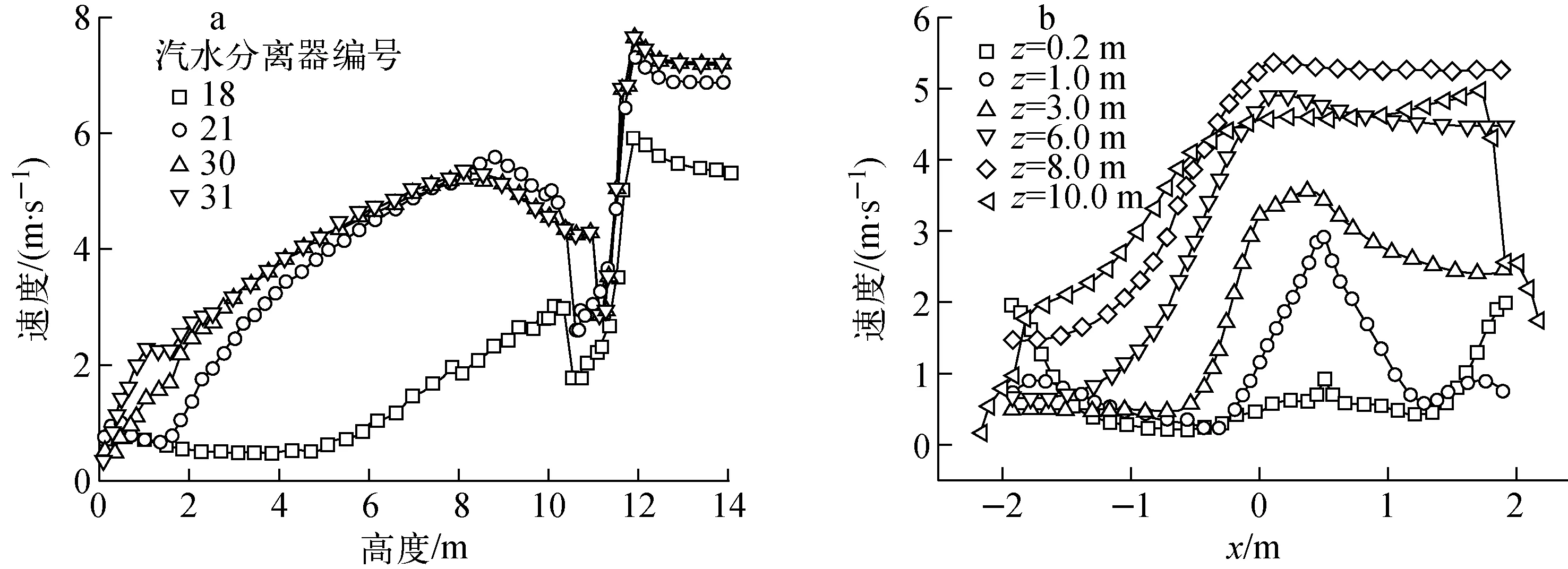
a——沿汽水分离器中心竖直线；b——沿对称截面上水平线

4 结语

本文采用多孔介质模型，对压水堆SG二次侧三维两相流场进行数值模拟，同时耦合一、二次侧一维换热，得到如下结论：

1) 采用多孔介质模型计算SG二次侧流场，相较于采用常规的CFD网格方法，可大幅节省计算量，并得到合理的数值解；

2) SG内冷热侧流体由于受热不均，导致两侧流体流动状态差别较大；

3) 汽水分离器内流动含气率分布极不均匀，其值介于0.05和0.62之间，此分布可为汽水分离器设计提供进口边界条件；

4) 通过计算得到弯管区速度场分布，可为U型管流致振动分析提供输入参数。

参考文献：

[1] PATANKAR S, SPALDING D. Heat exchanger design theory source book[M]. Washington D. C.: Scripta Book Co., 1974.

[2] SHA W, YANG C, KAO T, et al. Multidimensional numerical modeling of heat exchangers[J]. J Heat Transfer, 1982, 104(3): 417-425.

[3] PRITHIVIRAJ M, ANDREWS M. Three dimensional numerical simulation of shell-and-tube heat exchangers, Part Ⅰ: Foundation and fluid mechanics[J]. Numerical Heat Transfer, Part A: Applications, 1998, 33(8): 799-816.

[4] PRITHIVIRAJ M, ANDREWS M. Three-dimensional numerical simulation of shell-and-tube heat exchangers, Part Ⅱ: Heat transfer[J]. Numerical Heat Transfer, Part A: Applications, 1998, 33(8): 817-828.

[5] FERNG Y. Investigating the distribution characteristics of boiling flow and released nuclide in the steam generator secondary side using CFD methodology[J]. Ann Nucl Energy, 2007, 34(9): 724-731.

[6] FERNG Y M, CHANG H J. CFD investigating the impacts of changing operating conditions on the thermal-hydraulic characteristics in a steam generator[J]. Appl Therm Eng, 2008, 28(5): 414-422.

[7] FERNG Y M, YINPANG M, KANG J C. Thermal-hydraulic simulation of localized flow characteristics in a steam generator[J]. Nucl Technol, 2001, 136(2): 186-196.

[8] GETACHEW D, MINKOWYCZ W, LAGE J. A modified form of theκ-εmodel for turbulent flows of an incompressible fluid in porous media[J]. Int J Heat Mass Transfer, 2000, 43(16): 2 909-2 915.

[9] ANTOHE B, LAGE J. A general two-equation macroscopic turbulence model for incompressible flow in porous media[J]. Int J Heat Mass Transfer, 1997, 40(13): 3 013-3 024.

[10] CHANDESRIS M, SERRE G, SAGAUT P. A macroscopic turbulence model for flow in porous media suited for channel, pipe and rod bundle flows[J]. Int J Heat Mass Transfer, 2006, 49(15): 2 739-2 750.

[11] de LEMOS M J S. Turbulence in porous media: Modeling and applications[M]. London: Elsevier, 2012.

[12] MASUOKA T, TAKATSU Y. Turbulence model for flow through porous media[J]. Int J Heat Mass Transfer, 1996, 39(13): 2 803-2 809.

[13] KEETON L, SINGHAL A, SRIKANTIAH G. ATHOS3: A computer program for thermal-hydraulic analysis of Steam generators[M]. US: Electric Power Research Institute, 1986.

[14] MacADAMS W H. Heat transmission[M]. New York: McGraw Hill, 1954.

[15] GRIMISON E. Correlation and utilization of new data on flow resistance and heat transfer for cross flow of gases over tube banks[J]. Trans ASME, 1937, 59(7): 583-594.

[16] DITTUS F W, BOELTER L M K. Heat transfer in automobile radiators of the tubular type[J]. International Communications in Heat and Mass Transfer, 1985, 12(1): 3-22.

[17] DINGEE D A, BELL W, CHASTAIN J, et al. Heat transfer from parallel rods in axial flow[R]. Columbus: Battelle Memorial Institute, 1955.

[18] DINGEE D A, CHASTAIN J W. Heat transfer from parallel rods in an axial flow[C]∥ASME, Reactor Heat Transfer Conference. Oak Ridge, Tennessee: US Atomic Energy Commission, 1956.

[19] DWYER O, SHEEHAN T, WEISMAN J, et al. Cross flow of water through a tube bank at Reynolds numbers up to a million[J]. Industrial & Engineering Chemistry, 1956, 48(10): 1 836-1 846.

[20] 陶文铨. 数值传热学[M]. 2版. 西安：西安交通大学出版社,2001.

[21] LAUNDER B E, SPALDING D B. Lectures in mathematical models of turbulence[M]. France: Academic Press, 1972.

[22] SCHLICHTING H, GERSTEN K. Boundary-layer theory[M]. 8th ed. Germany: Springer, 2000.

[23] HOPKINS G. Verification of the ATHOS3 code against feedring and preheat steam generator test data[M]. US: Electric Power Research Institute, 1988.