三维空间液滴运动模型数值解法研究
2014-08-07薄涵亮
张 璜,薄涵亮
(清华大学 核能与新能源技术研究院,北京 100084)
液滴运动现象广泛存在于各种核能动力装置中。例如,蒸汽发生器内的汽水分离装置中就存在大量液滴运动。汽水分离装置的作用是将蒸汽发生器产生的湿蒸汽流进行干燥。欧美各国规定经汽水分离器干燥后的蒸汽湿度要小于0.25%,否则高速蒸汽流夹带着这些液滴会造成二回路管道、关闭件腐蚀,以及汽轮机的汽蚀,影响汽轮机寿命。因此,汽水分离装置的分离效率关系到核电系统运行的经济性和安全性。
常见的汽水分离装置有旋叶式分离器、重力式分离器和波形板式分离器,它们内部的液滴在蒸汽场中运动,流出或被分离器捕获。通过建立汽水分离器内液滴运动模型并对其进行求解,可得到液滴在分离器内部的运动轨迹和数目分布,进而能较为细致地研究分离器对液滴的分离机理,从而为设计高性能的汽水分离器提供理论依据。
不同学者采用的液滴运动模型虽不同,但该模型均可表述为1组一阶常微分方程。由于该组常微分方程通常无解析解,所以一般采用数值方法对其进行求解。庞凤阁等[1]采用高阶方程的Runge-Kutta(RK)算法对波形板内的液滴运动模型进行求解,得到了直径为7~10 μm的液滴运动轨迹。陈韶华等[2-3]采用定(单)步长的RK算法求解液滴运动模型,对重力分离空间内直径为0~350 μm的液滴和波形板分离器内直径为10.5~12.5 μm的液滴的运动行为均作了研究。王晓墨等[4]采用向前Euler算法求解液滴运动模型,得到了直径为10、20和900 μm的液滴在波形板内的运动轨迹。张谨奕等[5-6]考虑了液滴在三维空间中受到的Magnus升力和Saffman升力,采用4级4阶显式单步长RK算法对该模型进行数值求解,但只对波形板汽水分离器内直径大于50 μm的液滴的运动轨迹和分离效率进行了研究。
向前Euler算法虽易编程实施,但它是显式算法且仅有一阶精度,稳定性和精度均不能保证[7]。单步长RK算法虽能保证数值求解结果具有较高精度,但它依然是显式算法,数值稳定性不够好[7]。
针对以上不足,本文拟提出三维空间内液滴运动模型数值求解的一种算法,即算子分裂算法(OS算法)。本文首先简述适用于三维空间的液滴运动模型,随后详细介绍OS算法的数值离散格式,最后分别采用RK算法和OS算法对波形板汽水分离器内的液滴运动模型进行求解,从相容性、稳定性、计算精度和计算效率等方面对这两种算法进行比较。
1 三维空间液滴运动模型的数学表述
在三维空间中的单个液滴,不仅有相对于固定坐标系的平动,还有绕自身对称轴的转动和液滴表面的变形运动。在上述运动的同时,除了受到流场的作用力,还可能会对流场的变化产生影响。
因此,考虑到三维空间液滴运动的复杂性,本文提出如下假设:
1) 液滴和流场间无质量和热量交换;
2) 液滴为刚性圆球,在运动过程中不发生形变,因此液滴可看作刚体,其运动可分解为平动和转动;
3) 流场对液滴有作用力,而液滴在运动过程中对流场无影响。
基于以上假设,液滴的转动方程为:
(1)
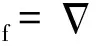
液滴运动方程为:
(2)
其中:md=πρdd3/6,ρd为液滴密度;vd为液滴速度;液滴所受曵力FD=πCDρf|vf-vd|(vf-vd)d2/8,CD为曵力系数;液滴所受惯性质量力FA=πρfd3[d(vf-vd)/dt]/12;液滴所受体积力FV=πd3(ρd-ρf)g/6,g为重力加速度;液滴所受Magnus升力FM=πCMaρfd3(vf-vd)×(ωd-ωf/2)/8,CMa为Magnus升力系数;液滴所受Saffman升力FS=1.615CSa(Rμ)2(ρfμf)0.5d2×|ωf|-0.5[(vf-vd)×ωf],CSa为Saffman升力系数,(Rμ)2表示液滴内部环流量对升力的影响,μf为流体动力黏性系数。
将以上各表达式代入式(1)和(2),并将方程左边系数归一化得:
(3)
其中:λ1=-15ρf/16π、λ2=3ρf/(4ρdd+2ρfd)、λ3=3ρf/(4ρd+2ρf)、λ4=[1.615(μd+2μf/3)2/(μd+μf)2(μfρf)0.5]/(ρdπd/6+ρfπd/12)、λ5=2(ρd-ρf)/(2ρd+ρf)为归一化系数;CM、CD、CMa、CSa等系数的值详见文献[5]。
式(3)即为本文需求解的三维空间液滴运动模型的数学表述式。
2 OS算法的离散格式
算子LA为:
(4)
算子LB为:
(5)
LA求解液滴的角速度变化和由曵力加速度引起的液滴速度变化;LB求解由Magnus升力、Saffman升力加速度和体积力加速度引起的液滴速度变化。这样就将求解式(3)的过程转换成分别求解式(4)和(5),这一步称为算子分裂。
假设时间步长τ=ti+1-ti,将(ωd,vd)记为Yd,从时刻ti到时刻ti+1,OS算法实施步骤为:
Yi+1=LAi(τ/2)LBi(τ)LAi(τ/2)·Yi
(6)
其中,LAi和LBi为离散的LA和LB算子。
OS算法需将式(6)表示的过程对时间离散。本文采用隐式算法求解算子LA,选取具有二阶精度的隐式梯形算法[7]离散式(4):
(7)
同时采用RK算法离散式(5),得:
(8)
引入定义:
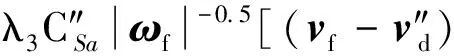
(9)
那么,K1、K2、K3、K4为:
(10)
OS算法针对式(3)的离散格式为式(7)和(8),对每一个时间步长的计算步骤为式(6)。
3 OS算法的验证
本文将RK算法[5]也用于求解式(3),以模拟直径为1~50 μm的液滴在波形板中的运动轨迹,从两种算法的相容性、稳定性、计算精度和计算效率等方面来验证OS算法的性能。
本算例中,采用无钩型波形板[1],其几何形状示于图1a。波形板的波数为2,入口及出口端长度均为L=10 mm,波形板间距H=12.5 mm,曲折角α=45°,折边B=25 mm,并定义w=B/H。假设波形板在冷态工况下工作,用不可压缩空气代替蒸汽[1],其密度ρf=1.225 kg/m3,动力黏性系数μf=1.789 4×10-5Pa·s;液滴密度ρd=998 kg/m3,动力黏性系数μd=9.98×10-4Pa·s。波形板内液滴和气体的运动可简化为二维,所以可忽略液滴受到的体积力,可令式(3)中λ5=0。
波形板内气体的二维流动满足Navier-Stokes方程,其连续性方程和动量守恒方程为:
(11)

(12)
其中,υf=μf/ρf为流体运动黏性系数。利用FLUENT 6.3.26对波形板内气相流场进行模拟,流动设置为稳态,入口速度分别设为3、5和7 m/s,黏性模式选用标准κ-ε湍流模型,固壁设置为无滑移边界,出口设置为充分发展流动,选用SIMPLE算法求解,各项残差设置为10-4 [8]。当入口速度为3 m/s时,计算结果采用Tecplot处理得到的波形板内流场的流线示于图1b。
为了模拟液滴在波形板内流场中的运动轨迹,需将FLUENT 6.3.26计算所得的流场速度和速度梯度保存为输出文件,作为求解液滴运动模型的已知流场速度和旋度。
3.1 OS算法相容性分析
隐式梯形法的局部截断误差为o(τ2)[7],RK算法的局部截断误差为o(τ5)[7]。
采用隐式梯形法和RK算法构造的OS算法的局部截断误差阶数推导过程为:采用OS算法求解式(3),当计算到第i步时,液滴的角速度和速度可写为yi=(ωdi,vdi),采用OS算法计算得到第i+1步的数值解为:
yi+1=[(yieLAτ/2+o(τ2))eLBτ+
o(τ5)]eLAτ/2+o(τ2)
(13)
利用式(3)得到第i+1步的精确解为:
(14)
式(14)减去式(13)所得结果即为OS算法的局部截断误差,最终有:
ο(τ2)
(15)
由式(15)可知,OS算法构造的离散格式的局部截断误差为o(τ2),与式(3)相容。
3.2 OS算法稳定性分析和RK算法时间步长比较
提出一个算法,首先必须保证它构造的离散格式和原方程相容。除此之外,更重要的是保证算法的收敛性。证明算法的收敛性往往非常困难[9],但只要对实际问题建立合适的物理与数学模型,则假定由相容与稳定的离散格式就能获得收敛的数值解[10]。
由于所求解的式(3)为非线性常微分方程组,因此本文仅讨论RK算法和OS算法的局部初值稳定性。在本文计算的波形板流场中,直径小于50 μm的液滴的平动雷诺数Red(Red=ρf|vf-vd|d/μf)和转动雷诺数Reω(Reω=ρf|ωd-ωf/2|d2/4μf)总体上分别小于6.2和1,且随着直径的减小,Red和Reω更加趋近于满足上述要求。此时可取CM=16π/Reω、CD=24/Red、CMa=1、CSa=1,在二维情况下,式(3)变为:
(16)
其中:α=4μf/d2;β=36μf/(2ρd+ρf)d2;γ=2ρf/(4ρd+2ρf);η=19.38(μfρf)0.5/πd(2ρd+ρf)。本文提出的OS算法主要针对直径小于50 μm的液滴,所以比较RK算法和OS算法稳定性时,可直接针对式(16)进行分析。
式(16)的系数矩阵Gcreep为:

图1 波形板的几何形状(a)和内部流场流线(b)
(17)
其中:ωd=(0,0,ωd);ωf=(0,0,ωf);vd=(vdx,vdy,0);vf=(vfx,vfy,0)。系数矩阵Gcreep包含要求解的未知数ωd、vdx和vdy,采用量纲分析估计Gcreep的大小。本文中,液滴速度和流场速度的量级为10 m/s,液滴角速度的量级为102rad/s,流场旋度的量级为103rad/s,液滴直径的量级为10-5m,结合已给出的液滴和流场的物性参数,系数矩阵Gcreep约为:
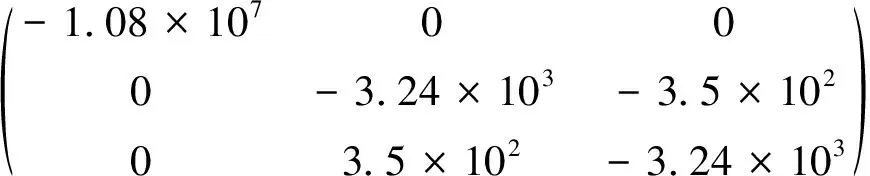
(18)
Gcreep特征值的实部为ζ1=-1.08×107、ζ2=ζ3=-3.24×103,可见式(16)是刚性方程。
用RK算法求解式(3)时,根据绝对稳定性条件[11]理论预测出计算不同直径液滴所需的最大时间步长τmaxTRK=-2.78/ζmin,ζmin为系数矩阵Gcreep的最小特征值(若特征值为复数,取特征值的实部)。通过数值实验,得到不同直径液滴情况下保持RK算法稳定的最大时间步长τmaxNRK,将两者同时列于表1。由表1可见,理论值和数值实验值很吻合。
OS算法的实施过程见式(6),ti+1时刻,yi+1=LAi(τ/2)LBi(τ)LAi(τ/2)·yi,令GOS=LAi(τ/2)LBi(τ)LAi(τ/2),则GOS的具体表达式为:
(19)
其中,χ=γ(ωf/2-ωd)-ηωf/|ωf|0.5。GOS的特征值ζ1=(1+ατ/2)2/(1-ατ/2)2,ζ2=ζ3=(1-βτ/2)2(1-τ2χ2/2+τ2χ4/24)/(1+βτ/2)2,要使OS算法稳定,只需保证GOS特征值的实部的绝对值小于1。已知α<0,β>0,那么必有|ζ1|<1,|ζ2|=|ζ3|=((1-βτ/2)2/(1+βτ/2)2)|1-τ2χ2/2+τ2χ4/24|<|1-τ2χ2/2+τ2χ4/24|,因此只需满足|1-τ2χ2/2+τ2χ4/24|<1就能保证OS算法稳定,其解为:

(20)
令τTOS=(12/χ2)0.5,不同液滴直径下的τTOS列于表1。由表1可知,τTOS的量级为10-1~10-3,而τmaxTRK和τmaxNRK的量级为10-6~10-9。值得注意的是,τTOS仅是保证OS算法稳定的充分条件,所以使OS算法稳定的最大时间步长τmaxOS≥τTOS。通过数值实验也发现,对于不同直径的液滴,τmaxOS均可放宽到1 s,因此也证实了上述观点。通过以上分析可知,OS算法可取的时间步长大于RK算法时间步长的取值,因此OS算法的稳定性优于RK算法。
3.3 OS算法计算精度和计算效率分析
由3.1节可知,RK算法的局部截断误差为o(τ5),而OS算法的局部截断误差为o(τ2),为保证OS算法依然具有较好的精度,对其时间步长选取如下:
(21)
RK算法的时间步长τRK取表1中给出的τmaxNRK,注意此时τOS仍比τRK大。
比较了两种算法计算得出的不同直径液滴在波形板内的轨迹形状。两种算法中,液滴进入波形板的速度和位置均相同。液滴进入波形板的速度与波形板内流场入口速度相等,液滴入射方向垂直于波形板入口,液滴初始位置在波形板入口处均匀分布。同一直径的液滴计算10个。图2为4种不同直径液滴以不同初始速度在波形板内的运动轨迹示意图。可见,两种算法得到的轨迹形状相似。

表1 τmaxTRK、τmaxNRK和τTOS的比较
记RK算法计算得到液滴恰好流出或被波形板捕获的位置(终端位置)为(xRK,yRK),OS算法得到液滴的终端位置为(xOS,yOS)。为了定量比较两种算法所得液滴终端位置的精度,分别定义x轴和y轴终端位置的相对误差为εx和εy:
(22)
两种算法计算所得不同直径液滴终端位置平均值及其相对误差列于表2~4。由表2~4可看出,εx在0.6%以内,εy在2.7%以内,可见OS算法和RK算法精度相当。
在计算表2的同时,记录每个液滴在波形板内经过完整轨迹所需的计算时间(取计算机的CPU耗时)并取平均值,定义RK算法计算单个液滴的平均CPU耗时除以OS算法的平均CPU耗时为CPU耗时倍数,最后所得结果列于表5。
由表5可见,3种工况的平均CPU耗时倍数均大于35。对于直径相对较小的液滴,如1 μm液滴,CPU耗时倍数可达300以上。因此,表2~5结果可证实,在保证OS算法和RK算法精度相当的前提下,OS算法的计算效率优于RK算法。

液滴初始速度:a——3 m/s;b——5 m/s;c——7 m/s
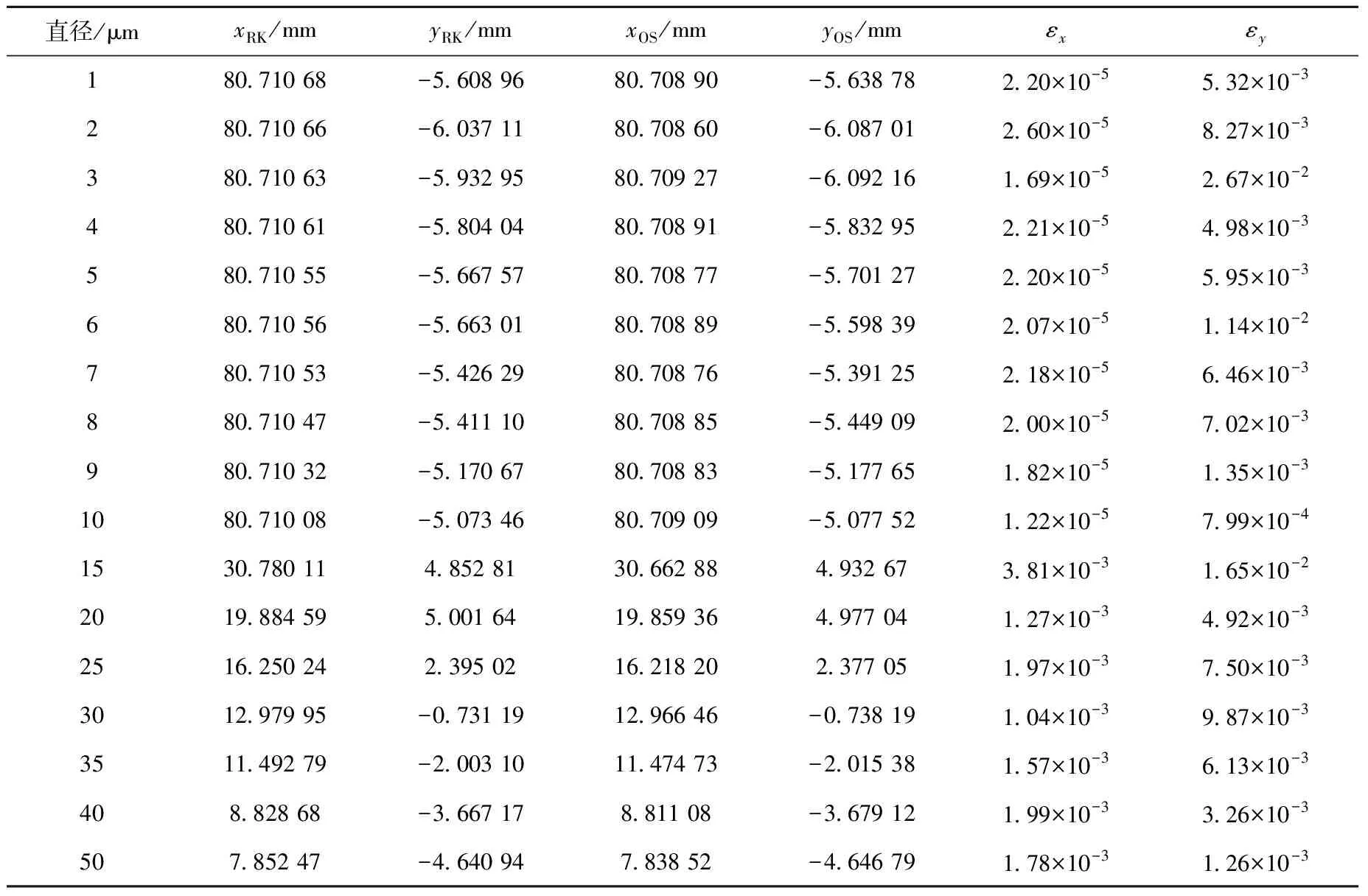
表2 液滴初始速度为3 m/s时两种算法计算所得不同直径液滴终端位置平均值及其相对误差
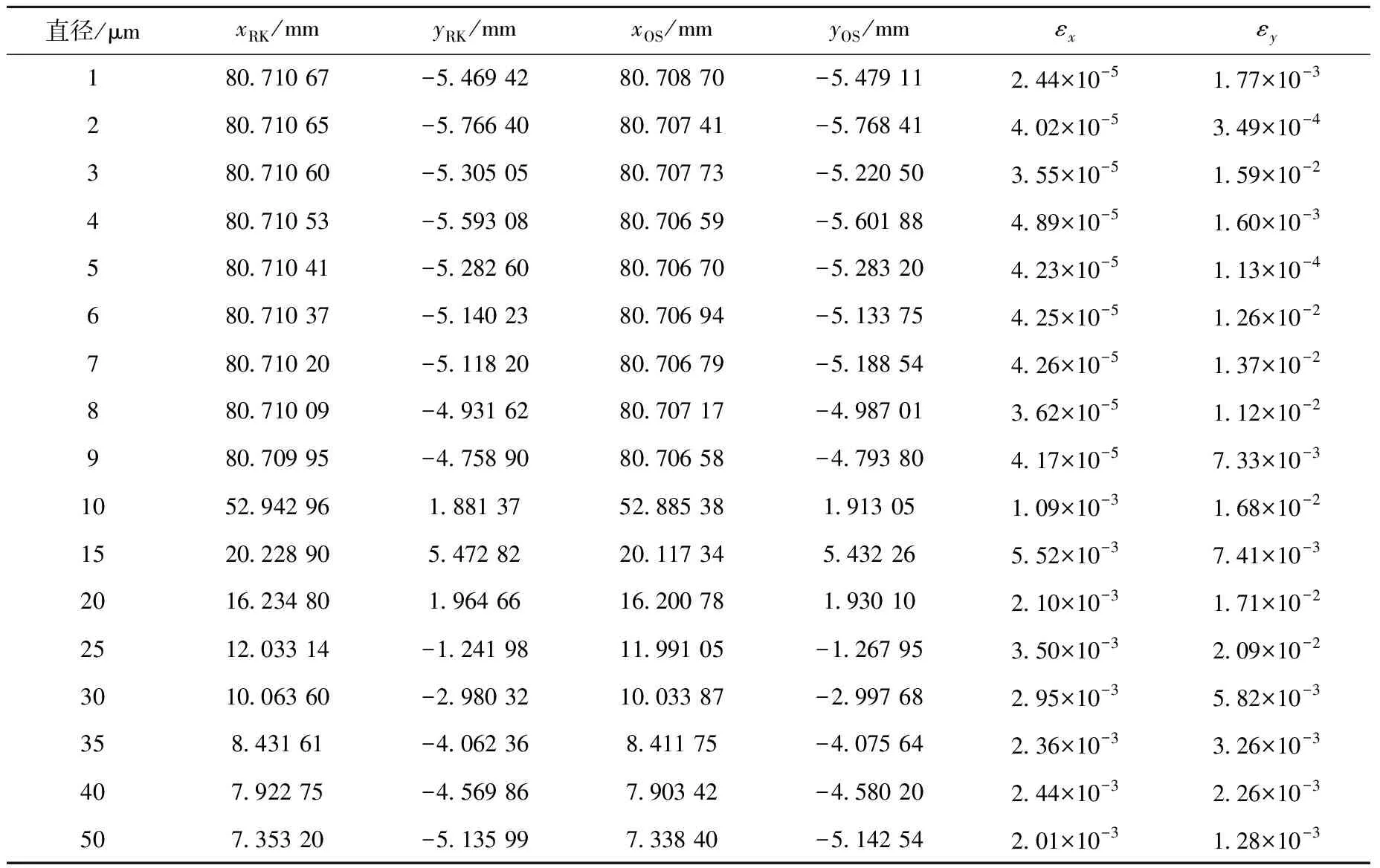
表3 液滴初始速度为5 m/s时两种算法计算所得不同直径液滴终端位置平均值及其相对误差

表4 液滴初始速度为7 m/s时两种算法计算所得不同直径液滴终端位置平均值及其相对误差
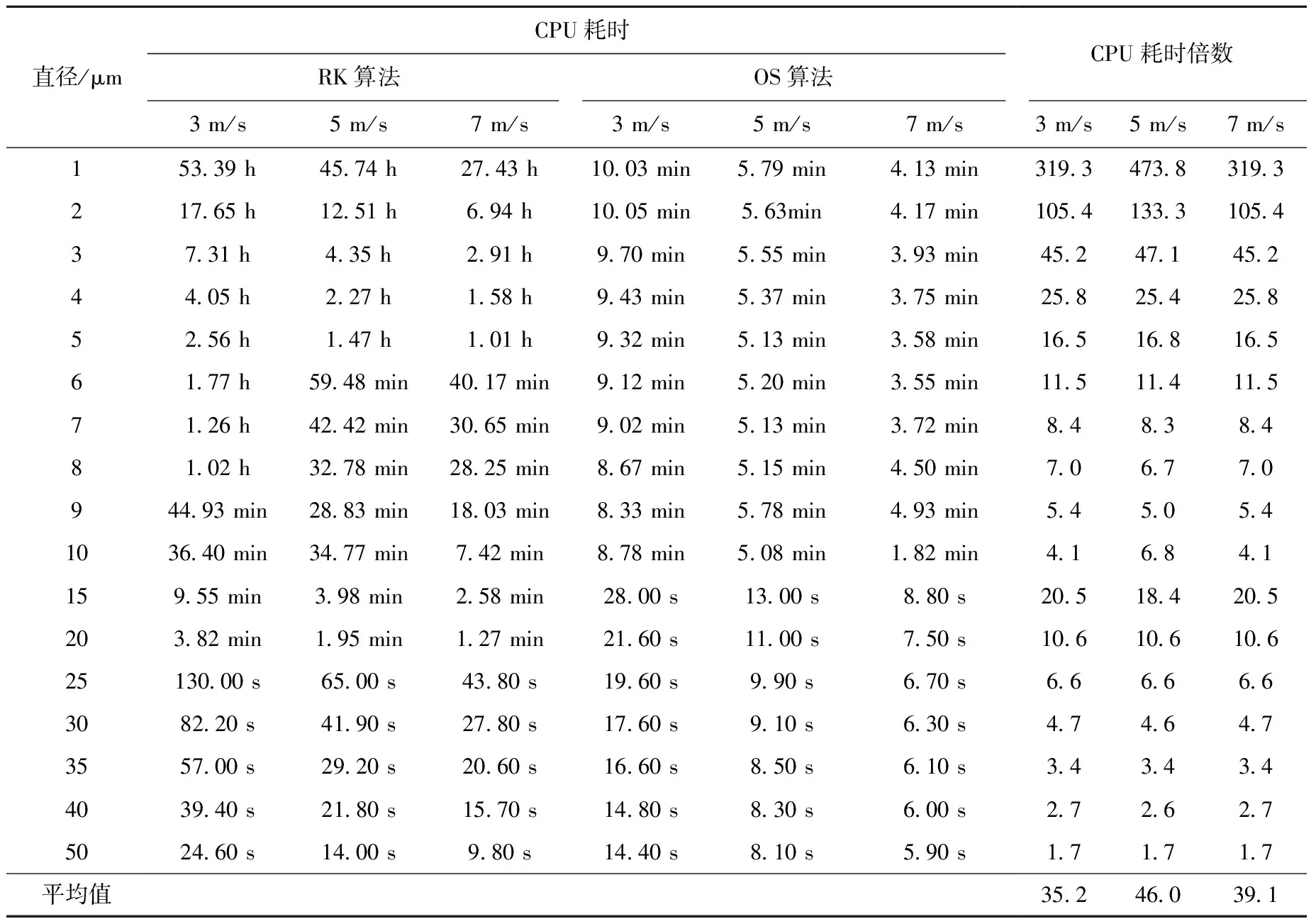
表5 两种算法对不同直径单个液滴的平均CPU耗时及CPU耗时倍数
4 结束语
本文针对三维空间液滴运动模型提出了一种新的数值求解方法——OS算法,并采用该算法求解波形板内液滴运动轨迹,同时与RK算法所得结果进行了对比。得到主要结论如下:
1) 本文构造的OS算法具有局部二阶精度;
2) 保持OS算法稳定的最大时间步长的量级可取10-1~10-3s,而保持RK算法稳定的最大时间步长的量级为10-6~10-9s,因此OS算法的稳定性优于RK算法;
3) 在计算精度相同的情况下,OS算法的计算效率优于RK算法。
因此OS算法的提出为数值求解三维空间液滴运动模型,进而计算波形板的分离效率提供了一种相对稳定、高效的算法。
参考文献:
[1] 庞凤阁,于瑞侠,张志俭. 波形板汽水分离器的机理研究[J]. 核动力工程,1992,13(3):9-13.
PANG Fengge, YU Ruixia, ZHANG Zhijian. The study of mechanism of corrugated baffles separator[J]. Nuclear Power Engineering, 1992, 13(3): 9-13(in Chinese).
[2] 陈韶华,黄素逸,赵绪新. PWR蒸汽发生器水滴重力分离研究[J]. 华中理工大学学报:自然科学版,1997,25(1):69-71.
CHEN Shaohua, HUANG Suyi, ZHAO Xuxin. A study on the gravity separation of water droplets in steam generators for PWR[J]. Journal of Huazhong University of Science and Technology: Nature Science Edition, 1997, 25(1): 69-71(in Chinese).
[3] 陈韶华,黄素逸,赵绪新. 波形板汽水分离器汽水两相分离机理研究[J]. 华中理工大学学报:自然科学版,1998,26(1):5-7.
CHEN Shaohua, HUANG Suyi, ZHAO Xuxin. On separation mechanism of steam water two phase flows in a steam water separator with corrugated baffle[J]. Journal of Huazhong University of Science and Technology: Nature Science Edition, 1998, 26(1): 5-7(in Chinese).
[4] 王晓墨,黄素逸. 波形板汽水分离器中液滴轨迹的数值模拟[J]. 核动力工程,2003,24(6):582-585.
WANG Xiaomo, HUANG Suyi. Numerical simulation of droplets track in separator with wave-shape vanes[J]. Nuclear Power Engineering, 2003, 24(6): 582-585(in Chinese).
[5] 张谨奕,薄涵亮,孙玉良,等. 三维空间液滴运动模型[J]. 清华大学学报:自然科学版,2013,53(1):96-101.
ZHANG Jinyi, BO Hanliang, SUN Yuliang, et al. Three-dimensional droplet motion model[J]. Journal of Tsinghua University: Science and Technology, 2013, 53(1): 96-101(in Chinese).
[6] 张谨奕,薄涵亮. 液滴模型在波形板汽水分离器中的应用[J]. 原子能科学技术,2012,46(增刊):776-781.
ZHANG Jinyi, BO Hanliang. Application of droplet model in wave-type vane steam separator[J]. Atomic Energy Science and Technology, 2012, 46(Suppl.): 776-781(in Chinese).
[7] 李大侃. 常微分方程数值解[M]. 杭州:浙江大学出版社,1994:21-42.
[8] 李嘉. 波形板汽水分离器的理论和实验研究[D]. 武汉:华中科技大学,2007.
[9] 陆金甫,关治. 偏微分方程数值解法[M]. 2版. 北京:清华大学出版社,2004:19-28.
[10] 陶文铨. 数值传热学[M]. 2版. 西安:西安交通大学出版社,2001:48-52.
[11] 李庆扬,关治,白峰杉. 数值计算原理[M]. 北京:清华大学出版社,2000:372-376.
