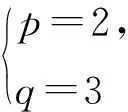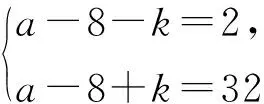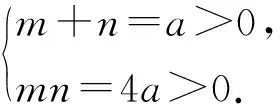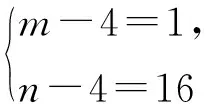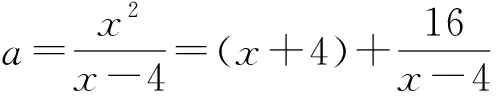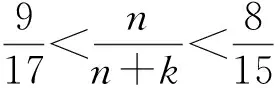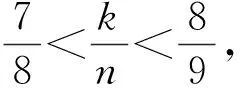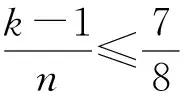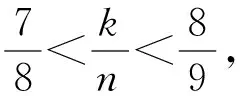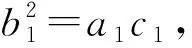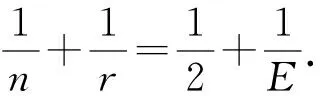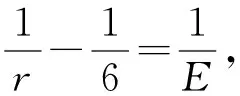初中数学融入数论教学的实践与思考

●

(永兴学校初中部 浙江富阳 311400)

在现行的初中数学教材体系中，几乎不涉及数论的内容和方法，但在竞赛和高中的自主招生中却频频出现，这不是命题者的偏好，而是由数论在数学中的地位以及在数学学习中的重要性决定的.本文结合笔者的教学实践谈谈对此的认识，回答为什么初中数学中要融入数论的教学，以及如何融入数论教学，以期抛砖引玉.

1 必要性与可行性

数论作为数学古老而又重要的分支，且不论其在现代计算机和信息技术中的广泛应用，就其内容和方法在数学学习中的重要性而言就是不可或缺的.在高中数列、排列组合、数学归纳法等内容的学习中都要用到有关整数的知识，而有关的概念和基础知识仅在小学时出现过，在整个初中阶段从未涉及，这不利于后续的数学学习，因此非常有必要在初中数学教学中融入和补充一些必要的数论内容.教学实践表明只要教师有意地进行渗透和补充，这是完全可行的，且能够取得较好的效果.

2 主要的内容

数论的内容和方法都很丰富，但教学时间却十分有限，选择哪些内容和方法来进行教学就成了一个大问题.笔者建议，可以参考全国初中数学联赛大纲中所列举的内容：十进制整数及表示方法；整除性，被2～5，8，9，11等数整除的判定；素数和合数，最大公约数与最小公倍数；奇数和偶数，奇偶性分析；带余除法和利用余数分类；完全平方数；因数分解的表示法，约数个数的计算；简单的不定方程和高斯函数等.

3 教学策略

3.1 结合日常教学逐步渗透

结合现行的教材,适时地进行渗透是非常必要的，比如在学习有理数或用字母表示数时，可以渗透奇数、偶数、余数、整数部分等概念(事实上，很多初中学生不知道奇数、偶数可以是负的，不知道-3除以5的余数是多少，错误地认为-2.1的整数部分是-2).在学习二元一次方程组时，可以渗透一次不定方程的概念及相关性质和求解的基本方法.在学习因式分解、一元二次方程时，可以渗透二次不定方程的概念和方法.下面通过具体的例子说明.

例1整数x，y满足方程2xy+x+y=83，则x+y=______或______.

(2010年“希望杯”全国数学邀请赛初一试题)

分析本题只需将原方程作局部的因式分解，变形为

(2x+1)(2y+1)=167.

因为167是质数，所以

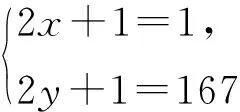
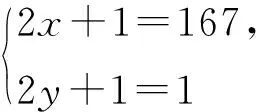
故x+y=83或x+y=-85.

此类问题可以在初一学习因式分解的应用课中有所渗透：一方面可以提高学生恒等变形的能力；另一方面可以体验整数的离散性.

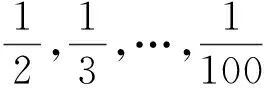
(2009年“希望杯”全国数学邀请赛初二试题)

分析本题要用到的知识点是：凡是分母的质因素仅含2或5的，化成小数后为有限小数；凡是分母的质因素既不含2又不含5的，化成小数后为纯循环小数.这99个分数中分母是2的x次方的有：2，4，…，64，共6个；5的x次方有：5，25，共2个；是10以及2和5但不是10和其他数的倍数的数有：10，20，…，100，共6个，因此分母能被2，5且只能被2，5整除的数共有6+2+6=14个，即能化为有限小数的有14个．分母含有2的共有100÷2=50个；分母含有5的共有100÷5=20个；分母同时含有2和5的共100÷10=10个，因此不含2和5的有99-50-20+10=39个，即纯循环小数有39个.

这里需要思考：将一个分数化为小数时有哪些情况；怎样的分数能化成有限小数；怎样的分数能化成纯循环小数；为什么分数化成小数要么有限要么循环.这些问题都可以在学习有理数、实数的概念时作为拓展问题让学生去思考、讨论和交流，可以帮助学生深入理解有理数和实数的概念.

例3已知二次函数y=x2+qx+p的图像与x轴交于不同的点A，B，顶点为C，且△ABC的面积S≤1．

(1)求q2-4p的取值范围；

(2007年浙江省温州中学自主招生试题)

分析(1)0

(2)由第(1)小题知，q2-4p=1,2,3,4.因为q2被4除余数为0或1，所以q2-4p被4除的余数也为0或1，从而q2-4p=1,4．这2个方程中符合题意的整数解有

例3的第(1)小题为中考要求，第(2)小题为竞赛要求，平时的作业中有这样的分层设计是非常好的，可以让不同的学生有不同的发展.

3.2 利用数学课外活动进行专题探究

当然仅在日常教学中渗透是不够的，对数论问题有深入了解和学习还需要利用课外活动时间，让学有余力的学生进行专题探究，若有机会听听专家的讲座那是最好的.比如：整除的判定、奇偶分析法、带余除法和利用余数分类、完全平方数、不定方程、二次方程的整数根和高斯函数等作为专题探究是很必要的，可以从专题探究中归纳出一般方法.例如，二次方程的整数根的问题解法灵活多样，可以通过典型例题来归纳提炼.

例4求所有正实数a，使得方程x2-ax+4a=0只有整数根.

(1998年全国初中数学竞赛试题)

分析这是一个典型的二次方程整数根问题，本质是二次不定方程.解决这类问题的常用方法可以通过这个例题归纳出来——首先由韦达定理可以得到a为整数.

解法1根据求根公式，判别式Δ必为完全平方数，因此可设Δ=k2，即

a2-16a=k2(k∈N)，

从而

(a-8-k)(a-8+k)=64.

因为a-8-k≤a-8+k，且a-8-k与a-8+k同奇偶(这里都为偶数)，所以

故a=25或a=18或a=16，经检验，都符合题意.

解法2本题涉及根与系数的关系，因此可以考虑用韦达定理.

设2个整数根为m,n(m≤n)，则

消去a得

mn-4m-4n=0,

从而

(m-4)(n-4)=16,

故a=25或a=18或a=16.

解法3考虑到参系数a是一次的，因而可以将它分离出来，得

因此，x-4为16的正约数：1,2,8，16,故a=25或a=18或a=16.

解法4将原方程直接局部因式分解，得

(x-4)(x-a+4)=-16，

可得a=25或a=18或a=16.

这4种解法在具体的问题中需要根据条件的特殊性(比如：参系数是有理数还是整数，方程有整根还是都是整根)灵活应用，选择合适的方法.

3.3 抓住核心的内容和思想方法

数论研究的是整数的性质，初中阶段核心的内容有整除性、利用余数分类、不定方程等.整数区别于有理数和实数的主要特点是整数具有离散性，因此解决整数问题的一个大的策略是通过一定的方式限定问题中整数的范围，将问题中的整数限定在一个较小的范围，然后通过逐个检验.

(2014年全国初中数学联赛试题)

因此

得

n≤144.

这是一个典型的整数最值问题，常用的思路是对问题的整体情况进行估计，找到变量的上界或下界，然后构造出一个实例说明此最值能够取得.这种先估计再构造的方法是求这类离散量最值的常用方法.

例6已知正整数a,b,c满足:1

(2013年全国初中数学联赛试题)

分析设a,c的最大公约数为(a,c)=d，则

a=a1d，c=c1d，

这里a1,c1均为正整数且(a1,c1)=1，a1

b2=ac=d2a1c1，

d(a1+b1+c1)=111，

即

d(m2+n2+mn)=111.

注意到m2+n2+mn≥12+22+1×2=7，因此d=1或d=3.

若d=1，则m2+n2+mn=111，验算可知只有m=1,n=10满足等式，此时a=1，不符合题意，故舍去；若d=3，则m2+n2+mn=37，验算可知只有m=3,n=4满足等式，此时a=27,b=36,c=48，符合题意.因此，所求的b=36.

利用整除的性质、分类讨论、限定范围等都是在处理整数问题时常用的思想方法.

3.4 激发学习兴趣和积极性

数论的内容往往方法独特，学生在学习中经常会遇到困难，教学中要注意激发学生的兴趣和积极性，渗透相关的数学史，介绍数学家的故事和研究成果，往往会有较好的效果.比如：华罗庚自学成才的故事、陈景润和哥德巴赫猜想、山东大学数学系王小云教授在密码学上取得成就——10年破解世界五大著名密码，为信息安全作出了杰出的贡献等.这些精彩而传奇的故事往往能够激发学生学习的热情和增加学生在学习中克服困难的信心和勇气.让学生看到所学内容的应用价值也是激发学生兴趣的好方法之一.比如，古希腊柏拉图时候就知道确有5个正多面体存在，即正四面体、立方体、正八面体、正十二面体、正二十面体，那么为什么有且仅有这5种正多面体呢?课外活动中可以介绍相关内容，并让学生积极思考、讨论，如果学生觉得毫无思路，又有强烈求知的愿望，那么教师就可以介绍证明方法.现证明如下：

证明对于正多面体，假设它的各面都是正n边形，而且每一个顶角处有r条边相遇.这样就有：

式(1)的右边系数2是因为每边出现在2个面中，式(2)的右边系数2是因为每边通过2个顶角.把式(1)和式(2)代入欧拉公式中，得

(3)

显然n≥3，r≥3，因为多边形至少有3条边，而在每个顶角处也至少有3条边相遇.但n>3，且r>3又是不可能的，若

学生会被这样的证明所震撼，没想到解决问题的工具是自己所熟悉的不定方程，感受到数论的应用价值，感受到数学思维的魅力，从而获得学习数论的兴趣和动力.