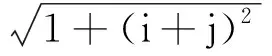妙用构造 巧解赛题
2014-08-07
●
(诸暨中学 浙江诸暨 311800)
所谓构造的思想方法,是指在对问题进行透彻分析、对其实质进行深刻了解的基础上,借助于逻辑分析或长期积累的经验,发挥高度的想象力和创造性,将问题从原来的模式转化为更能反映其本质特征的新模式的思想方法.构造思想是一种很活跃的创造性思想方法,它能沟通数学各个不同的分支,实现跨度极大的问题转化.应用构造思想解题的关键有2个:一是要有明确的方向,即构造的目的;二是要弄清条件的本质特点,以便重新进行逻辑组合.构造的方法有很多,其中以构造函数、方程、图形、模型、算法等最为常见.本文试通过案例叙述构造法在数学竞赛中的应用.
1 构造方程,多元问题主元化
方程是解数学题的一个重要工具,根据数学题设中量的关系,构造出方程,使原来复杂的数学问题变得直观合理、简洁易解.数学题中的有些问题表面上看似乎与方程无关,但通过分析题中各个量之间的关系就可以构造出方程,然后通过方程来巧解数学问题.
例1求方程x3+y3-x2y2-(x+y)z=0的所有解(x∈N*,y∈N*,z∈N).
(2013年全国高中数学联赛吉林省预赛试题)
分析原方程无论是看作关于x的方程还是关于y的方程,都是三次方程,不易分解,难以下手,但注意到
x3+y3= (x+y)(x2-xy+y2)=
(x+y)3-3xy(x+y),
若记a=x+y,b=xy,则原方程可看作关于b为主元的二次方程,即
b2+3ab-a2(a-z)=0.
考虑到x,y,z都是整数,从而
Δ=9a2+4a2(a-z)=a2(4a+9-4z)
为完全平方数.又4a+9-4z是奇数,故可设
4a+9-4z=(2t+1)2,
则
a=t2+t+z-2,b=a(t-1) (t≥2).
因为(x-y)2=(x+y)2-4xy=a2-4a(t-1),且
[a-2(t-1)-2]2≤a2-4a(t-1)<
[a-2(t-1)]2,
显然[a-2(t-1)-1]2≠a2-4a(t-1),所以
[a-2(t-1)-2]2=a2-4a(t-1),
从而t=2,z=0,即x=y=2,z=0.
本题通过换元,不断地转换原方程的形式,构造出结构更为简单的方程,使问题得到解决.
2 构造函数,隐性问题显性化
函数是中学数学知识的一个中心,函数图像可以看作是研究函数性质的一个工具,进而解决一类相关问题.构造函数法是运用函数概念和性质构造辅助函数进行解题.构造函数的前提是熟悉函数的概念,牢固掌握各类初等函数的性质,构造过程要求我们选择恰当的函数,并准确地运用函数性质,以便快捷无误地解决原问题.
例2设实数a,b满足3a+13b=17a,5a+7b=11b,证明:a (2001年罗马尼亚奥林匹克数学竞赛试题) 分析3个底数两两互素且指数不全相等的指数方程很难求解,考虑将其放缩为指数相同的不等式.先假设a≥b,则13a≥13b,5a≥5b,由3a+13b=17a,得 3a+13a≥17a, 即 同理由5a+7b=11b,得 5b+7b≤11b, 即 从而b>1.因此a<1 向量是非常有用的一个工具,它具有几何形式和代数形式的双重身份,对一些比较复杂的数学问题,若能把它转化为向量,用向量的性质来解决问题,则会事半功倍. 例3设a,b,c为正实数,且满足abc=1,试证明: (第36届IMO试题) 分析原不等式等价于 根据不等式左边的特征,联想到向量数量积,可以构造三维向量 根据向量性质|m·n|≤|m||n|,可得 用几何图形来解决问题是构造思想的一个重要方面.对于本身不具备图形的一些数学问题,由于它的条件中数量关系有明显的几何意义或通过某种方式可以将问题转化成几何图形,则可以借助几何图形的性质来研究,从而获得解决.它的实质就是“数转化为形”,借助图形来实现解题的目标. 例4已知a,b,c,d是正实数,求证: (第52届白俄罗斯奥林匹克数学竞赛试题) 又直线PQ的方程为 (b+d)x-(a+c)y+(bc-ad)=0, 从而原点到直线PQ的距离为 由|OP|≤|OR|+|RP|,|OQ|≤|OR|+|RQ|得 |OP|+|OQ|≤ |RP|+|RQ|+2|OR|= |PQ|+2|OR|, 得证. 构造算法主要指直接设计、构造出一种可行的计算、作图的程序步骤,在有限次内能够实现所构造的对象.这样,不仅证明了存在性,而且可以按照程序在有限步骤内确定存在的对象.我们借用“算法”这一术语,不妨称之为构造“算法”. 例5设正实数a,b,对于任意的n∈N*,设xn为[an+b]在十进制中各位数字之和,证明:序列{xn}包含一个由常数构成的子列. (2002年罗马尼亚奥林匹克数学竞赛试题) 10k+a, 即 10k=[ank+b]≤10k+[a]. 当k足够大时,有10k-1>a.因此xnk是集合{0,1,2,…,[b]}中的某个数t的各位数字之和加1.因为k可以取无穷多个值,而t是有限的,所以有无穷多个k,使得[ank+b]的各位数字之和相同. 在数学竞赛中有很多特殊模型,在解一些非常规题时,我们需要拓展思维,合理联想,为题目临时建立恰当的解题模型.这种构造方式是将问题中的条件、数量关系,在已构造的模型上实现并得到解释.这样就实现了问题的证明,或转化为在所构造的“模型”上相应问题的证明. 例6一条链子上有2k颗白珠子和2m颗黑珠子.若将这条链子剪断把珠子均分给2个人,每人得k颗白珠子和m颗黑珠子,问至少要剪几刀才能保证上述分法能实现. (2000年以色列奥林匹克数学竞赛试题) 分析选定一颗白珠子将其编号为1,然后按顺时针方向依次给每颗珠子编号:2,3,4,…,直到最后一颗,编号为2(k+m),然后给每一颗珠子编组:1号珠子,连同它后面的k+m-1颗珠子,共k+m颗珠子编为一组,称为1号组;2号珠子,连同它后面的k+m-1颗珠子编为2号组;…共2(k+m)组,每组均有k+m颗珠子.且满足:(1)每组中的白珠子不可能都多于k颗;(2)相邻2组中白珠子数目最多相差1.现在假设没有一组的白珠子数目为k.由条件(1)知,必存在2个相邻组A,B,A中白珠子数小于等于k-1,B中白珠子数大于等于k+1,即A和B的白珠子数至少相差2,矛盾!因此,必有某组恰好含有k颗白珠子和m颗黑珠子,把这一组2头剪下来即可.故至少剪2刀. 为了证明某种对象的存在性,找到这种对象的一个特例,即能实现证明.另外为了证明一个命题不真,也只需构造一个特例——“反例”说明即可.选择题设条件中特殊、极端的情形,常常是构造特例与反例的关键. 例7集合A={n!+n|n∈N*},集合B是集合A对N*的补集.问:是否存在各项都在集合B中的无限项等比数列?说明理由. 分析首先考虑最特殊的等比数列,例如{an}等,不符合;接着考虑{a·bn}这样的等比数列,如:3,6,12,…,3×2n-1,…符合题意.下面只要用反证法证明:此数列中的任一项均不在集合A中即可.设 3×2n-1=k!+k=k[(k-1)!+1], 则 k|3×2n-1, 从而k=1,2,3,6,2i-1,3×2i-1(3≤i 易验证k=1,2,3,6,均不符合. 若k=2i-1(3≤i 3×2n-1=2i-1+(2i-1)! 即 3×2n-i=1+(2i-1-1)!, 式子2边同时模3,得0≡1+0(mod 3),矛盾! 若k=3×2i-1(3≤i 3×2n-1=3×2i-1+(3×2i-1)! 即 2n-i=1+(3×2i-1-1)!, 式子2边同时模2,得0≡1+0(mod 2),矛盾! 故数列{3×2n-1}中的任一项不能写成k!+k的形式,即这样的等比数列存在. 图1 例8证明:对每个自然数n(n≥3),都能够在平面上找到满足下列2个条件的n个点: (1)任意2个点之间的距离都是无理数; (2)任意3个点都是面积为有理数的非退化三角形的顶点. (第28届IMO试题) 分析要在平面上找满足题意的n个点,不妨在我们比较熟悉的曲线或曲线组合上去找,例如在抛物线y=x2上选n个点Pi(i,i2)(i=1,2,…,n),这n个点满足题设的2个条件,验证如下: (1)任意2个点Pi,Pj之间的距离是 (2)由于抛物线是凹的,故任意3个点Pi,Pj,Pk都不共线,△PiPjPk为非退化的,从而 显然S△PiPjPk是有理数. 笔者例举了一些常见的构造法,当然还可构造数列、复数、对偶式、不等式、恒等式等等,而且构造法也不是上述问题的唯一解法,即使对同一问题还可从不同角度去构造.构造法体现了数学的创新思维,巧在“构造”,难也在“构造”,它要求学生针对题目的特征、对掌握的知识进行整体分析,构造出基于问题又在思维上有突破的方法,这是对学生思维方式的极好挑战.因此,在解题教学时,教师若能启发学生从多角度、多渠道进行联想,则能得到许多构思巧妙、新颖独特、简捷有效的解题方法而且还能加强学生对知识的理解,培养思维的灵活性,提高学生分析问题的创新能力.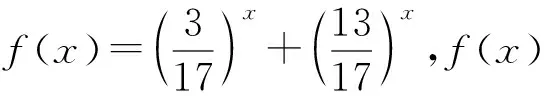
3 构造向量,表象问题本质化
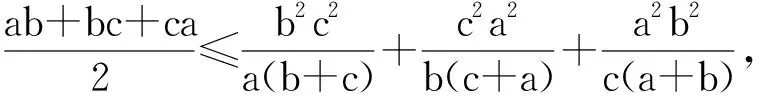
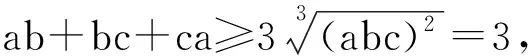
4 构造图形,代数问题几何化
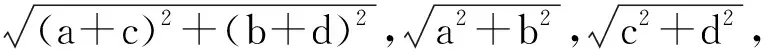
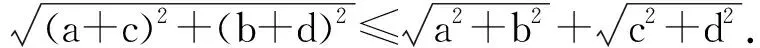
5 构造“算法”,无穷存在型问题步骤化
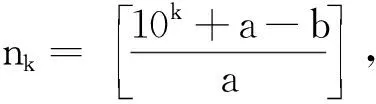
6 构造实际操作模型,非常规问题模型化
7 构造特例,不真问题证明简单化