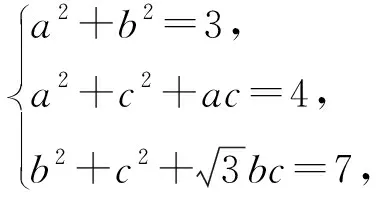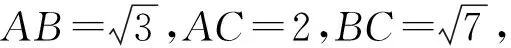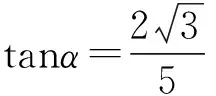例谈构造三角形在高中数学竞赛中的应用
2014-08-07
●
(东阳中学 浙江东阳 322100)
三角形是平面几何中最简单的图形之一.三角形的许多性质、定理,如内角和定理、边角不等关系、余弦定理、正弦定理、面积公式等是解决问题的基本工具.高中数学竞赛中的许多问题,可以根据已知条件转化为某种特殊的三角形,即构造三角形来解决,这是数形结合思想在解题中的充分体现,需要解题者对题目中的条件认真分析、实现转化,并通过丰富的想象力和创造力来完成构造.
1 构造三角形解求值问题
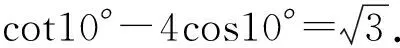

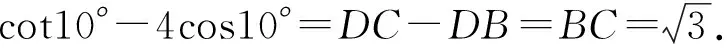
例2求cos210°+cos250°-sin40°sin80°的值.
(1991年全国高中数学联赛试题)
解因为10°+50°+40°+80°=180°,所以可构造一个以60°,40°,80°为内角的△ABC,其3条边长分别为a,b,c,如图2所示.在△ABC中,运用余弦定理得
a2+b2-2abccos60°=c2,
即
a2+b2-ab=c2,
由正弦定理得
sin280°+sin240°-sin40°sin80°=sin260°,

注:将正弦定理的结论a=2RsinA,b=2RsinB,c=2RsinC代入余弦定理结论得
sin2A=sin2B+sin2C-2sinAsinBcosA,
本例中sin280°+sin240°-sin40°sin80°=sin260°,恰为一个特例.

图1 图2 图3
2 构造三角形求最值问题

解将已知式变形为

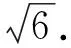

3 构造三角形证明不等式问题
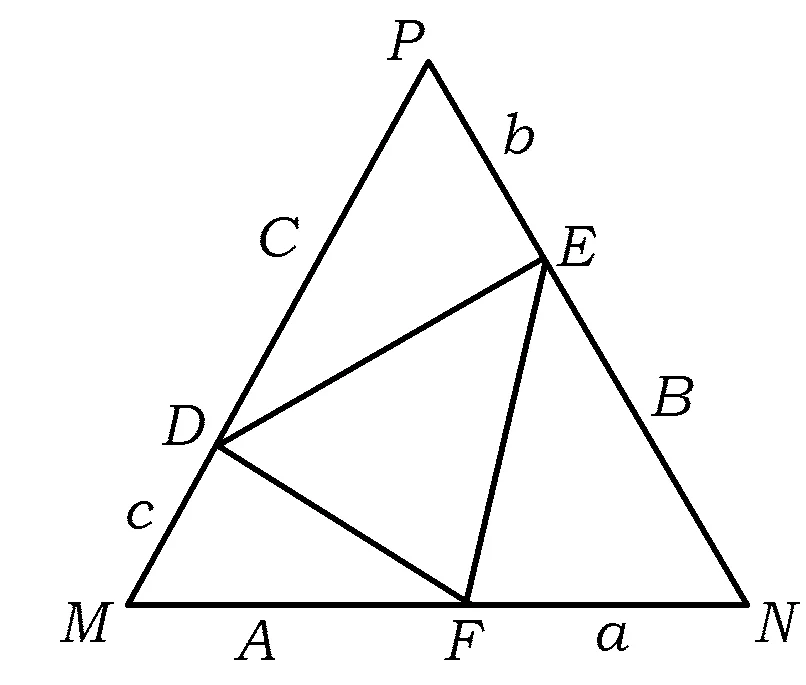
图4
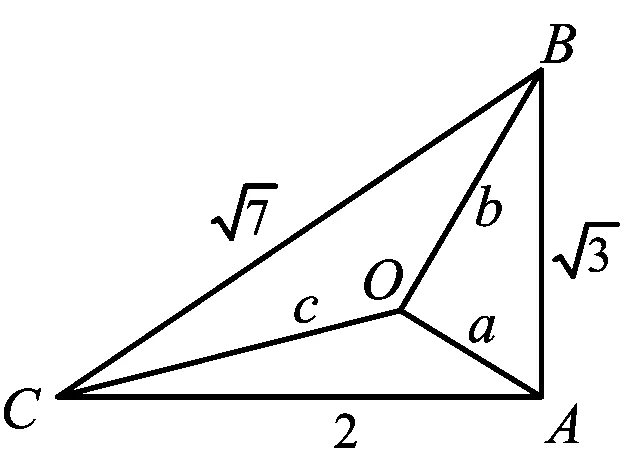
例4正数a,b,c,A,B,C满足条件:a+A=b+B=c+C=k,求证:aB+bC+cA (第21届全苏中学生数学竞赛试题) 分析抓住条件a+A=b+B=c+C=k,构造以k为边长的正△MNP来解决. 证明构造以k为边长的正△MNP,使得3条边满足条件MF=A,NE=B,PD=C,NF=a,PE=b,MD=c,如图4所示,则 S△DMF+S△FNE+S△EPD 从而 aB+bC+cA 分析本题若用代数方法将不等式化简,则比较繁琐,观察到当待证不等式右端小于等于0时,不等式显然成立,而当右端为大于0时,以a,b,c为边恰好构成一个三角形,而且右端的形式与海伦公式很接近. 证明当(a+b-c)(b+c-a)(c+a-b)≤0时,原不等式显然成立. 要证明上式可利用函数y=sinx的凹凸性,因为函数y=sinx在x∈(0,π)上是凹函数,从而 注:例4和例5中联想三角形中边的关系构造三角形,充分利用三角形的面积公式解题. 图5 现在边A0An上取n-1个点,设为A1,A2,…,Ai,…,An-1,满足Ai-1Ai=ai(1≤i≤n),则A0An=Sn.于是对于A0An上任一点Ai,在△AA0Ai中,由余弦定理得 从而 (2014年浙江省高中数学竞赛试题) 分析由方程的形式特点,联想勾股定理、余弦定理,可构造直角三角形. 图6 本文主要介绍了几例构造三角形解决的数学竞赛问题,通过构造三角形,可以建立起各种数学知识之间的联系与相互转化,激发学生的兴趣.但构造三角形解题并不是万能的,这需要合理地分析题目中的条件,并联想能否与三角形的有关性质产生联系.
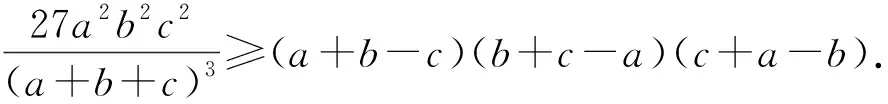
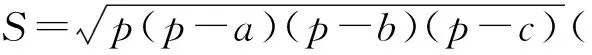

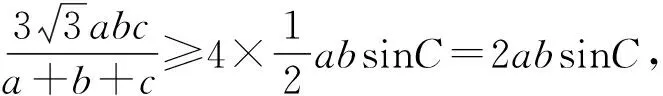
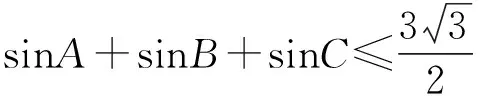
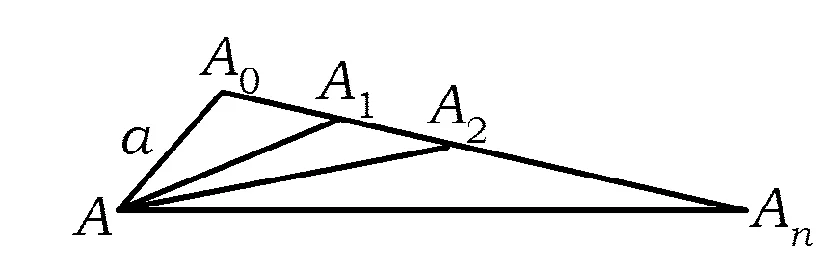
4 构造三角形解数列问题
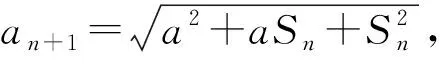

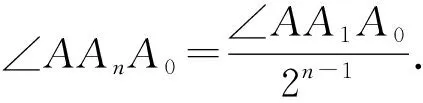
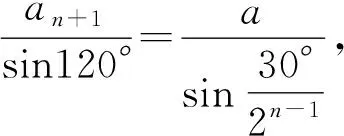
5 构造三角形解方程