例说函数图像的变换

●

(余姚市实验学校 浙江余姚 315400)

函数图像的变换主要是指平移、翻折(轴对称)、旋转(含中心对称)、伸缩等，这是研究函数性质的重要手段和内容，在高中阶段的学习中有充分的探索与应用．函数概念的抽象性决定了它是学生学习的难点，其广泛性决定了它又是学习的重点，而图像的直观性可以降低理解的难度.数形结合，可以促进学生更好地理解与掌握函数的本质．

本文通过剖析几个以函数图像变换为背景的例题，把散碎的知识、技能、思想、方法等进行列举、归纳和提炼，在解决个案的基础上，从整体上系统地把握函数图像的变换，更加接近函数的本质，也为高中进一步学习奠定良好的基础．

例1定义{a,b,c}为函数y=ax2+bx+c的“特征数”．如：函数y=x2-2x+3的“特征数”是{1,-2,3}，函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}．

图1

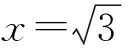
(2012年浙江省杭州市萧山中学自主招生试题)

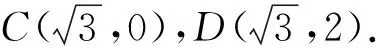
(3)二次函数为

即

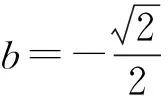
综上所述，实数b的取值范围为

评注函数图像的平移可以通过关键位置的点的平移来实现控制．根据“两点确定一条直线”，只需2个对应点的平移就可以求出平移后的直线解析式．实践中，往往采用“平行直线斜率相同”的结论，选择1个对应点的平移，这个点常选在坐标轴上，比如本例中第(1)小题，从点A(0，1)到点B(0，-1)．若是抛物线，则根据二次项系数不变，抓住顶点的平移，求得平移后的抛物线解析式．

例2我们知道：将二次函数y=-3x2的图像先向上平移1个单位，再向右平移2个单位，所得图像的函数表达式为

y=-3(x-2)2+1.

将一次函数y=3x的图像先向下平移1个单位，再向左平移2个单位，所得图像的函数表达式为

y=3(x+2)-1．

类比以上函数图像的平移：

(2013年浙江省宁波市重点高中推荐生面试试题)

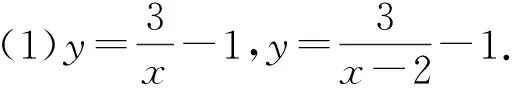
评注本例的设计意图是将平移规律从熟悉的直线与抛物线的平移，类比到双曲线的平移，从特殊点上升到一般点．通过观察、类比,得到结论：函数图像向上平移a(a>0)个单位长度时，常数项加上a;函数图像向下平移a(a>0)个单位长度时，常数项减去a；函数图像向左平移b(b>0)个单位长度时，自变量加上b;函数图像向右平移b个单位长度时，自变量减去b．渗透着更一般的表达形式：把y=f(x)上下平移得y=f(x)+a(当a>0时向上平移，当a<0时向下平移)；把y=f(x)左右平移得y=f(x+b)(当b>0时向左平移，当b<0时向右平移)．

例3将二次函数y=-2(x-1)2-1的图像先向右平移1个单位，再沿x轴翻折到第一象限，然后向右平移1个单位，再沿y轴翻折到第二象限，……，以此类推，如果把“向右平移一个单位，再沿一条坐标轴翻折一次”记作一次变换，那么二次函数y=-2(x-1)2-1的图像经过2 010次变换后得到的图像的函数关系式为

( )

A．y=2(x+3)2+1 B．y=2(x-2)2+1

C．y=-2(x+2)2-1 D．y=-2(x-1)2-1

(2010年安徽省合肥一中自主招生试题)

分析平移和翻折不改变抛物线的形状、大小，但关于x轴翻折时改变开口方向．开始时二次函数图像的顶点为(1，-1)，第1次操作后顶点为(2，1)，其图像解析式为

y=2(x-2)2+1；

第2次操作后顶点为(-3,1)，其图像的解析式为

y=2(x+3)2+1；

第3次操作后顶点为(-2，-1)，其图像的解析式为

y=-2(x+2)2-1；

第4次操作后顶点为(1，-1)，其图像解析式为

y=-2(x-1)2-1.

回到了起点，从而发现规律：每4次一个循环变化，2 010=4×502+2，应与第2次结果重合．故选A．

评注顶点是抛物线的要点，求抛物线的轴对称图形转化成确定顶点的轴对称点．抛物线y=a(x+m)2+k的顶点为(-m,k)，其关于x轴的对称点为(-m，-k)，关于y轴的对称点为(m,k)．因此它关于x轴的对称抛物线为

y=-a(x+m)2-k；

关于y轴的对称抛物线为

y=a(x-m)2+k．

更一般地，函数y=f(x)的图像关于x轴对称的图像的解析式为

y=-f(x)；

函数y=f(x)的图像关于y轴对称的图像的解析式为

y=f(-x)．

例4若函数y=|x+1|+|x-a|的图像关于直线x=1对称，则a的值为

( )

A.3 B.2 C.1 D.-1

(2009年浙江省余姚中学自主招生试题)

分析设f(x)=|x+1|，g(x)=|x-a|，它们都可以由m(x)=|x|的图像平移得到．因为y=f(x)+g(x)关于直线x=1对称，所以f(x)与g(x)一定关于直线x=1对称，关键点(-1，0)与(a，0)关于直线x=1对称，因此a=3.故选A．

评注函数图像关于直线x=m对称，同样可以利用特殊点的对称来处理．当然也可以运用以下结论：若f(x)=f(2m-x)或f(m+x)=f(m-x)，则f(x)的图像关于直线x=m对称．特别地，当m=0时，图像关于y轴对称．

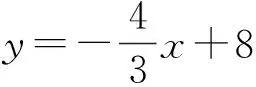
(2012年江苏省海门中学自主招生试题)

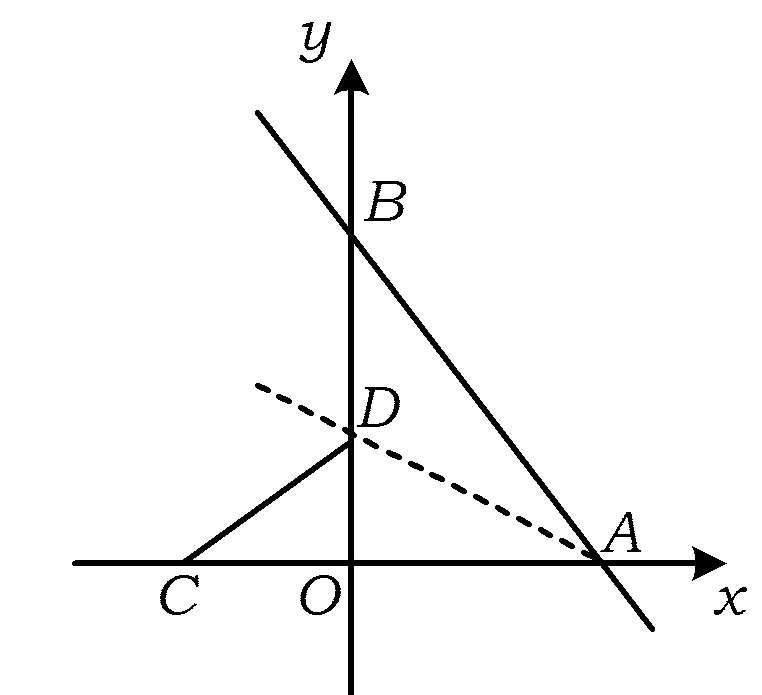
图2

分析如图2，先求得点A(6，0)，B(0，8)，C(-4，0)，再求得点D(0，3)，因此CD的解析式为

点D坐标的求法列举如下：

方法1由AD平分∠BAO得

从而

方法2设OD=m，则

CD=BD=8-m，

由勾股定理得OC2+OD2=DC2，

解得

m=3.

其实，还可以这样求得CD的解析式：由∠DCO=∠ABO可得2条直线的斜率互为负倒数，再把点C(-4，0)代入即可．

评注函数图像关于斜直线对称，运算量要增加很多，针对题设，寻找关键点，核心在于充分利用轴对称的对应相等关系，求出对称点的坐标，从而确定新图像的解析式．如果是关于直线y=x或y=-x对称，可参考如下结论：函数y=f(x)的图像关于直线y=x对称的图像的解析式为y=f-1(x)，函数y=f(x)的图像关于直线y=-x对称的图像的解析式为y=-f-1(-x)．

例6点P为抛物线y=x2-2mx+m2(m为常数，m>0)上任意一点，将抛物线绕顶点G逆时针旋转90°后得到的新图像与y轴交于点A,B(点A在点B的上方)，点Q为点P旋转后的对应点．

(1)当m=2，点P的横坐标为4时，求点Q的坐标；

(2)设点Q(a，b)，用含m，b的代数式表示a；

(3)如图3，点Q在第一象限内，点D在x轴的正半轴上，点C为OD的中点，QO平分∠AQC，AQ=2QC，当QD=m时，求m的值．

(2011年云南省玉溪市数学中考模拟试题)

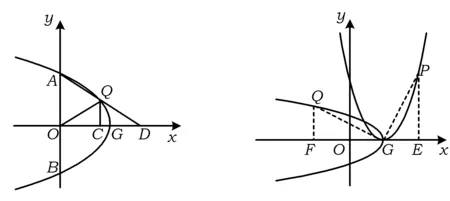
图3 图4

分析(1)如图4，作PE⊥x轴于点E，QF⊥x轴于点F，联结GP，GQ，易证△PEG≌△GFQ，从而FQ=GE=2，FG=PE=4，故点Q(-2，2).

(2)类比第(1)小题的解法，得P(m+b,m-a)，代入原抛物线的解析式y=x2-2mx+m2，得a=m-b2.

图5

(3)如图5，延长QC至点E，使CE=QC，易证△OCE≌△DCQ，△AQO≌△EQO，得

AO=OE=QD=m.

把A(0，m)代入第(2)小题的结论a=m-b2，得0=m-m2，故m=1或m=0(不合题意，舍去)．

评注从第(1)小题的特殊值到第(2)小题的一般式，再到第(3)小题的应用，较好地体现了核心数学思想．对大多数学生来说本题难度较大，教学中应指导学生抓住旋转中的相对不变量，利用全等三角形对应线段相等，建立对应点坐标的联系．对于学有余力的学生，不妨引导他们尝试平移纵坐标，使点O与点G重合．

例7已知抛物线l1：y1=ax2+x+m，抛物线l2：y2=(a+1)x2+x+n，且l1与l2互相经过对方的顶点，则a的值为______.

(2014年“希望杯”全国数学邀请赛九年级试题)

分析设l1，l2的顶点分别为(p,q)，(s,t)，分别代入直线l1，l2得

y1=a(x-p)2+q，

y2=(a+1)(x-s)2+t，

从而

t=a(s-p)2+q,

q=(a+1)(p-s)2+t.

2个式子相加，得

(a+a+1)(s-p)2=0，

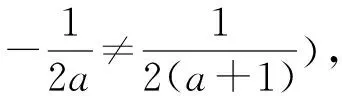
评注通过对特殊点(2个顶点)与函数解析式的代数运算，求得l1与l2是关于某点成中心对称的(对称中心是它们顶点连线段的中点)，从数的视角推理形的存在．

综合上述各例解析可知：函数图像的平移、翻折、旋转常常通过研究特殊点的平移、翻折、旋转，来把握其变换规律，计算结果．作为优秀的学习者，可以在这个探索过程中做个有心人，结合图形直观与代数计算，努力从对特殊点的考察升级到对一般点的研究，逐步上升到对规律性进行概括的高度．并能在实践中灵活运用，成为体现数形结合思想的主战场．