从师生“解题对话”谈排列组合的学习与教学

● (太湖高级中学 江苏无锡 214125)

排列组合是离散数学中的重要内容之一，是高中数学的重要组成部分.排列组合的内容丰富，具有一定的挑战性，可培养学生猜想、概括等思维能力，发展学生的创造力.笔者在日常教学中发现，学生在解决相应问题时，容易出现各种各样的错误.笔者记录了与学生对话的4个片段，每个片段都以学生的提问开始，在对话的过程中，暴露学生的错误，通过笔者的纠正和引导，最终使学生达到正确思考.

1 解题对话

片段1

问题14名司机和4名售票员，被分配到4辆不同路线的公交车上，每辆公交车有1名司机和1名售票员，有多少种不同的方案？

生：我的答案是4×4×4=64.先选1名司机，共4种选法；再选1名售票员，共4种选法；最后选1辆公交车，也是4种选法.故答案为64.

(该学生用树状图把所有的情况罗列了出来.)

生:还有别的情况吗？

师：我们不妨把4名司机分别记为a1,b1,c1,d1，售票员记为a2,b2,c2,d2，公交车记为a3,b3,c3,d3，而a1a2a3只是司机、售票员和公交车的一个配对，并不是4名司机、4名售票员被分配到4辆不同路线的公交车上的一种方案.

生：是的，没理解题目的意思.那这个问题该怎么思考？

师：可将4辆不同的公交车看成4个不同的位置，现在要把4名司机放在这4个位置上，每个位置1个人，这是哪一类问题？

生：4个位置排4个人，排列问题.

师：那有多少种情况？

师：那将4名售票员放到4个不同的位置呢？

排列组合中的问题来源于日常生活，与生活、生产实践密切相关.如何根据情景将实际问题转化为数学问题至关重要.片段1反映了学生在解决问题的过程中常常误解文字表述、错误理解情景.那么如何正确理解题目所给的情景呢？一是正确读题，找出题目中的关键词；二是复述题意，复述题意可反映学生对题目的理解程度，有利于提高学生的概括能力和数学语言的表述能力；三是采取某种方法模拟情景，将实际问题数学化，利用具体的图形、表格表示实际问题，用数学符号或数学表达式表示题目中的数量关系.

片段2

问题2将4封信投入3个不同的邮筒，有多少种投法？

生：老师，本题参考答案是34，而我认为是43.

师：那你的理由是什么？

(学生先在草稿纸上画3个方格表示邮筒.)

生：第1个邮筒可能有4封信放入，第2个邮筒也可能有4封信放入，第3个邮筒也可能有4封信放入,根据分步计数原理,所有的投法应为4×4×4=64种.

师：第1个邮筒可放入4封信，那你一旦放入1封信，第2个邮筒肯定没有4封信可放.

生(陷入思考)：那第1个邮筒可能放0封信、1封信、2封信、3封信、4封信，共5种情况，第2个邮筒也有5种情况，第3个也一样.由分步计数原理，知共53种放法.

师：按照你的说法，会出现每个邮筒都有3封信的情形，但总共才有4封信.

生：那该怎么想呢？

师：4封信投入3个邮筒，最终的结果是什么？

生：信在邮筒中.

师：对，信在邮筒中.第1封信有几个去向？

生：3个.

师：第2封信呢？

生：3个，第3、第4封信都是3个去向.

师：一次投1封，几次能把信投完？

生：4次.

师：那也就是说，完成投信这件事有4步:第1步有3种方法，第2步也有3种方法，第3、第4步也各有3种方法.利用分步计数原理,共有34种不同的投法.

生：这样啊，从结果看信的去向.

师：对，从结果看问题，比如5名学生报名参加4项体育比赛，每人限报1项，报名的方法有多少种？

生：结果是学生报上体育项目，第1个学生有4种报法，第2个学生有4种报法，……共计45种报名方法.

师：若5人争夺4项体育比赛的冠军，获得冠军的情况可能有多少种？

生：结果是4项比赛冠军产生，第1个项目的冠军可能是5人中的任何1个人，有5种可能，第2个项目也是这样，……共有54种可能性.

师：这是一类重复排列问题，如果在同一个含n个元素的集合中依次进行k次选取，而且选过的元素还可再选，则一共有nk种不同的选取方式，但是一定要弄清楚是从哪个集合中进行重复选取.投信的例子可看作从集合{邮筒1，邮筒2，邮筒3}中重复选4次，5名学生报名的例子可看作从集合{项目1，项目2，项目3，项目4}中重复选5次.

排列组合计数问题有很多种，如排列问题、组合问题、重复排列问题、染色问题等等.学生在学习过程中难免出现混淆，在解决问题时，经常出现不顾具体问题的含义，乱套用公式，乱用策略.为了避免此类错误，学生要理解公式或策略的来龙去脉，知道其适用范围.

片段3

问题36本不同的书分给甲、乙、丙3个人，每人至少1本，有多少种不同的分法？

师：这里面有很多的重复，举个例子：给6本不同的书编号，分别为1，2，3，4，5，6.从6本书中选3本给甲、乙、丙3个人，甲得到1，乙得到2，丙得到3；剩余3本书再分时，甲得到4，乙得到5，丙得到6；这样甲得到的是1，4，乙得到的是2，5，丙得到的是3，6.利用你的方法，也会出现这样一种情形，甲、乙、丙先分别得到4，5，6，再将剩余3本书分给3个人时，甲得到1，乙得到2，丙得到3.这样2种操作是一个情形，就出现了重复.

生：怎么思考才能做到不重复呢？

师：6本不同的书分给3个人，每人至少1本，先不管每个人具体分到什么书，从每个人得到书的数量上考虑，会出现哪些情况？

生：1本、1本、4本；1本、2本、3本；2本、2本、2本，共3种情况.

师：比如第1种情况，哪个人得到4本呢？

生：这3个人都有可能，不过可以先不考虑这种情况，先将书分3组，然后再分给3个人.

师：你说的对,那我们先分组，6本书分成3组：1本、1本、4本，如何分呢？

生：平均分组会出现次序.

师：对的，那再分给3个人呢？

师：另外2组也可类似计算，不妨试试.

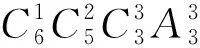
师:那所有的情况呢？

生：全部加起来，即

片段4

问题46名学生排成一行照相，其中女生2名，男生4名，女生甲不排在最左端，女生乙不排在最右端，问共有多少种不同的排法？

生：对啊，确实遗漏1种情况.

师：这个问题可以这样考虑：女生甲不能排在最左端，女生乙不能排在最右端，那就是说最左端和最右端都是特殊位置，甲、乙是特殊的人员.我们可以按某一个“标准”进行分类：甲在最右端，乙在最左端；甲在最右端，乙不在最右端；甲不在最右端，乙在最左端；甲不在最右端，乙不在最左端，共4类情况，且每一类情况之间没有重复.

片段3和片段4是学生在解决排列组合问题时常犯的错误：重复或遗漏.如何才能有效地避免重复与遗漏的现象呢？文献[1]中指出面对一些头绪纷繁的计数问题，将该问题划分为一类一类较为简单的情况，分别计数，然后再求总和.而一类一类的划分，没有重复没有遗漏，我们称之为一个有效划分.利用集合表示就是把集合B分成一些子集B1,B2,B3,…,Bk，使得

(1)B1∪B2∪B3∪…∪Bk=B；

(2)B1∩B2=φ,B2∩B3=φ,…,Bk-1∩Bk=φ.

也就是说不仅这些子集的并是B，而且这些子集之间两两互不相交.

正确分类可避免重复和遗漏.将复杂的情形简单化，分为几类，每类都便于计数.此外，还有很多其他类型的错误，如文献[2]中指出：忽视排列顺序、混淆对象、列举不全、凭直觉回答、计算错误、忘记公式、代错参数、画错树形图、误用组合数性质等等.面对学生在学习排列组合出现的错误，作为教师要思考平时的教学采取何种策略才能提高教学质量，提升教学效果.

2 教学策略

2.1 原理概念作基石

2个基本计数原理是学习排列组合的基础，学生在学习这2个原理时，教师必须利用大量的实例引导学生理解这2个基本原理，用实例概括、归纳这2个原理，同时让学生分清这2个基本原理的条件和结论，比较它们的异同.在排列和组合教学时，首先让学生分清什么是排列问题、什么是组合问题，搞清排列和组合的区别与联系；其次理解排列数和组合数的含义，能利用排列数、组合数结合这2个基本计数原理解决问题.

2.2 题型模式识别

笔者认为，排列组合问题的情景很多，而情景是造成学生学习障碍的主要原因之一，能适当总结一类问题及其解决方法，可有效地提高解决问题的能力.笔者结合文献[3]对中学排列组合问题给出13种模式(见表1)，学习掌握这些模式可提高解决问题的能力，也可加深对排列组合概念的认识.

表1 中学排列组合问题的13种模式

上述策略不是相互孤立的，而是互相为用的，有时解决某一问题需用上述的某2个策略，也有时需综合利用多个策略才能解决问题.

2.3 数学思想领航

模式识别只是用一种方法解决一类问题，但问题很多，“死记”模式就把知识学“死”了.排列组合中问题虽多，但解决排列组合问题的一般思路是：(1)先组合，再排列；(2)先分类，再分步；(3)先特殊，再一般.深刻理解基本概念与原理，灵活利用解题模式、数学思想，从而将待解决问题转化为已有模式，利用已知求解未知.

参 考 文 献

[1] 苏淳.同中学生谈排列组合[M].合肥：中国科学技术大学出版社，2011.

[2] 黄兴丰,李士锜.从符号学的视角分析学生解排列组合题的错误[J].数学教育学报，2008，17(4):33-35.

[3] 王凯.例谈排列组合问题的常用解法[J].中学数学，2014(3)：92-94.