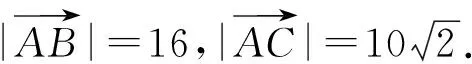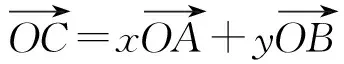一道高考模拟题的解法探究和溯源拓展

●

(惠贞书院 浙江宁波 315016)

数学课本中，很多习题都有很深的背景，有进一步拓展其数学功能、发展功能和教育功能的可行性，教学中应尽力寻找高考题、模拟题在课本中的“影子”，充分挖掘课本习题的潜能，以激发学生的潜力．

本文通过对2014年浙江省宁波市高三数学一模考试理科第17题的解法探究，寻找它在课本中的“影子”，追根溯源对其解法进行探究，并作一些简单拓展．

1 考题再现

例1

考试结束后，笔者问了基础一般的学生，他们都没有很好的思路，感觉不知所措，能做出来的学生是平时比较拔尖的．

由此可见，这样一道高考模拟题对普通学生的“杀伤力”有多大，同时也反映了我们在高考的复习中对教材的挖掘之浅，对课本习题的研究浮于表面．

图1

2 追根溯源

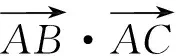
分析

此题为人教A版教材必修4第108页B组第4题．因为

3 解法探究

平面向量类试题基本上可以从以下4个方面入手：

(1)传统法(基底法)；

(2)几何意义；

(3)建系；

(4)其他性质．

笔者从以上这4个方面结合三角形的一些知识对本题解法进行探究．

解法1

(基底法)由

得

从而

本题无明显的几何意义，但我们看到△ABC已确定，各边大小和夹角都可以求出来．

解法2

(几何意义)在△ABC中由余弦定理得

BC2=AC2+AB2-2AC·AB·cos∠BAC，

即

在△ABC中由正弦定理得

即

从而

得

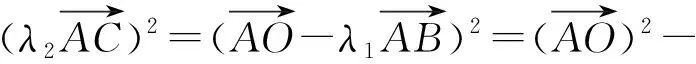
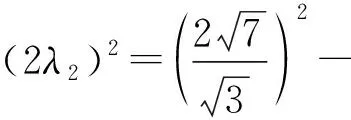
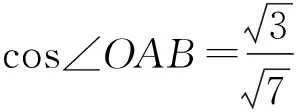
(1)

同理可得

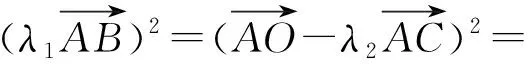
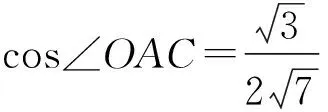
(2)

联立式(1)，式(2)得

从而

解法3

得

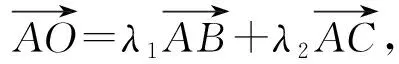
即

得

从而

对于思路4(其他性质)：笔者还没有想到一些重要的性质可以适用，暂时还未能有更巧妙的方法．

综合以上，我们可以很清晰地看到：传统法(解法1)、建系(解法3)更易于被学生接受，因此我们在平时复习备考的过程中要立足双基，追求通性通法，这在浙江高考中尤为重要．

4 开拓创新

我们可以再从以下几个角度作一些拓展：(1)三角形化;(2)函数化;(3)方程化;(4)最值化．以研究教材来促进高考复习，开拓创新．

变式1

分析

变式2

分析

得

16x+8ycosA=8，

即

2x+ycosA=1.

同理可得

4xcosA+2y=1,

联立方程可得

从而

至此我们把目标函数转化为关于cosA的函数，下面只要求出cosA的范围即可．

在锐角△ABC中，设a为角A所对的边.由于角A,B,C均为锐角，可得

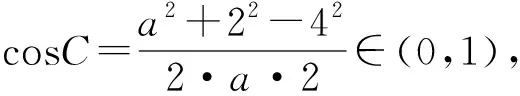
又在三角形中满足

得

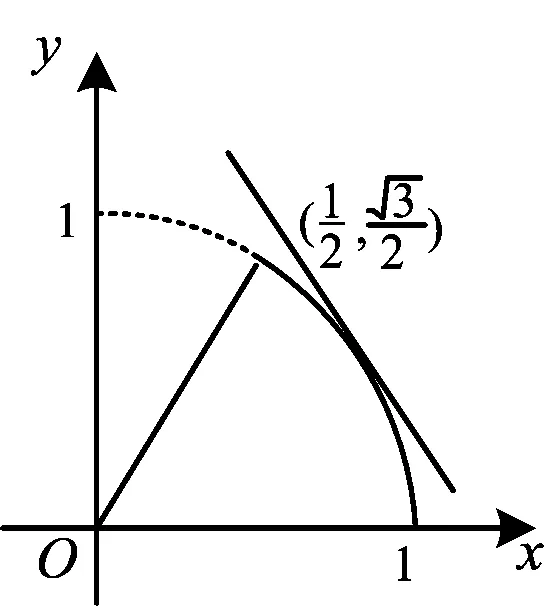
2

从而

由12

从而

此题中最后考了分式函数的最值问题，利用“换元法”化归为常用函数，这也是2013年浙江省数学高考理科第21题考查过的通性通法，充分体现了“函数与方程”的思想．

变式3

分析

即

解

同变式2，可得

于是

图2

变式4

( )

分析

此题在变式3的基础上引进“最值”问题.结合三角函数的“工具性”,考查了类似于恒成立问题．这与2013年浙江省数学高考理科试题第7题有“异曲同工”之处．

又因为∠AOB=60°，所以

x2+xy+y2=1,

配方可得

令

即

图3

可得

图像如图3所示.由

得

因为u=x+λy存在最大值，所以

解得

故选C．

本题还可以利用三角换元，得到u关于θ的函数．

可设

即

从而

得

由

得

即

于是

现在，各校都在提倡高效课堂，从教材挖掘这一角度来说大有文章可作，而且近几年的高考试卷与教材关联越来越密切，很多试题的背景都来源于课本又高于课本.作为一名高中数学教师，对课本例题和习题要有针对性地进行探索发现，并作相应拓展，做到低起点、高要求，在师生共同研究的氛围中提高学生分析问题、创新问题的能力，使学生能学会知识的迁移和创新，能够透过现象发现本质．

“你若发现了一株蘑菇，便可以发现一群蘑菇．”作为教师，要善于抛出一株蘑菇，引导学生寻找一群蘑菇，让学生在探究中感受知识的活力，在感悟中发展自己的思维与能力，真正做到走出题海，让学生感受到课本就是一个很大的宝库，最终走进研究性学习．