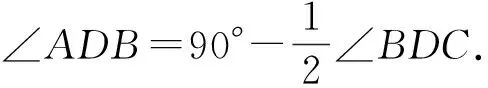初中数学奥林匹克问题中的老鼠尾巴
2014-08-07
●
(舟山教育学院 浙江舟山 316000)
数学解题学上有一个著名典故:把寻找题解比作“怎样去抓藏在石堆里的老鼠”,此即“老鼠尾巴”的由来.这个典故由前苏联的著名数学家塔尔塔科夫斯基首先提出来,通俗地说,就是寻找解题合适的切入口的形象生动的比喻,就是在一个问题面前“怎么去想”的一种关键性想法.“老鼠尾巴”就是可能显露、启示问题解决的切入口的一种隐含信息.
塔尔塔科夫斯基说:“有2种方法可捉住藏在石堆里的老鼠:一是把石堆的石头一块一块地搬开,……;二是围绕石堆不停地来回走动,留心观察,看在什么地方露出了老鼠尾巴没有.”解数学题总是依据问题的条件、结论去思考,从而寻找到解题的入手途径.生活实际并不是每个问题都会有明显的“老鼠尾巴”露出在石堆外边的,但也确实有些问题,它的条件或结论有某种特殊性;仔细分析后才知正是解题入手的好途径,这就是这里所说的“老鼠尾巴”.
“老鼠尾巴”的教学意义是很大的:对学生,可以学会在审题时,如何抓住关键性条件的内涵,找到切入口;对教师,从此就有了讲数学题的诀窍了:抓老鼠尾巴!
1 “对称性”是一种“老鼠尾巴”
图形的对称性、代数式子的对称性,在数学中很常见,它们都是一种在解题时可以利用且应该加以利用的“老鼠尾巴”.
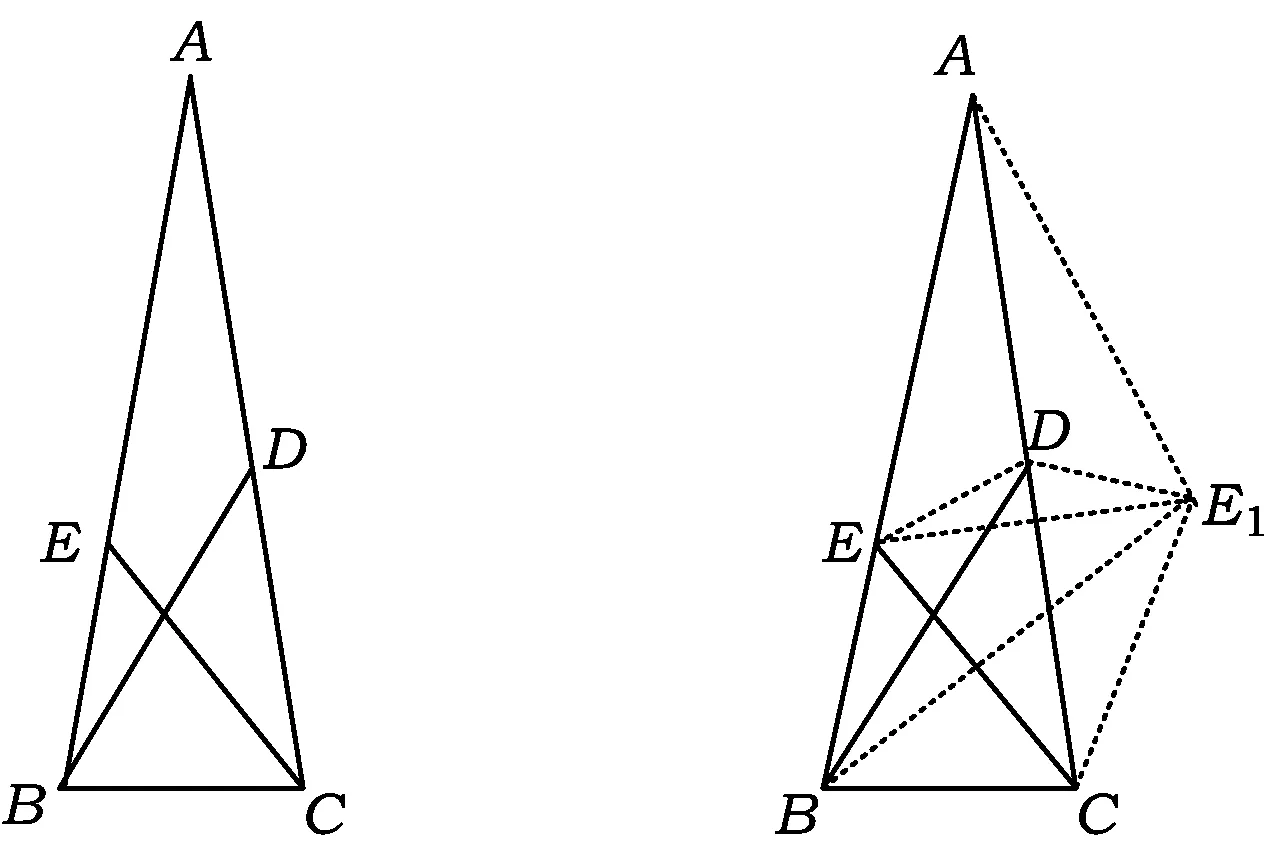
图1 图2
例1
如图1,设△ABC为等腰三角形,∠B和∠C都是80°,点D,E分别在AC,AB上,BD和CE把∠B和∠C各分成2个部分,∠DBC=60°,∠ECB=50°,求∠EDB的度数.
老鼠尾巴:等腰三角形本是对称图形,在原图的基础上,再对称地添加一些线段,正是完成本题求解的关键.
分析
由∠ECB=50°,∠ACB=80°,知∠ECD=30°.如图2,若把△ACE以AC为对称轴,作出它的对称图形△ACE1,就能得到等边三角形△CEE1(这里添加的辅助线是解开本题的钥匙).于是可推得△BCE1≌△BEE1,BE1为CE的垂直平分线,从而
BC=BE,∠EBD=20°=∠DBE1,∠EAD=∠E1AD,
故点D为△ABE1的内心.因此
∠AED=∠AE1D=50°,
∠EDB=∠AED-∠EBD=50°-20°=30°.
2 “任意性”是一种“老鼠尾巴”
数学问题的条件中,涉及“任意”的题目也是十分常见的,如:任意一点、任意实数等,这些都是一定要加以利用的“老鼠尾巴”.
例2
在平面上取4个点A,B,C,D,已知对于任意一点P,都满足不等式PA+PD≥PB+PC.证明:点B和点C在线段AD上,且AB=CD.
老鼠尾巴:“点P为平面上任意一点”表明点P可在平面上的任意位置,既可与点A重合,也可与点D重合,不论点P在何处,都满足题中的不等关系.如何利用好“点的任意性”,是解决本题的关键.
分析
若点P与点A重合,则
AD≥AB+AC,(1)
若点P与点D重合,则
AD≥DB+DC.(2)
对于三角形,有三边关系
AD≤AC+CD,(3)
AD≤AB+BD.(4)
式(1)+式(2),得
2AD≥AB+AC+DB+DC,(5)
式(3)+式(4),得
2AD≤AC+CD+AB+BD,(6)
比较式(5)与式(6),得
2AD=AB+AC+DB+DC,
从而
AD=AB+BD,AD=AC+CD,
即点A,B,C,D共线.
至此,式(1)~(4)都是等式.这时易证:点B和点C必须都在线段AD上,且AB=CD,其他情形(如点B在AD的延长线上等)不满足条件.
3 (整数的)“有理性”或“无理性”是“老鼠尾巴”
主要可以利用:无理数加有理数是无理数;无理数乘非零有理数一定是无理数等性质.
例3

(1)当a,b,c,d满足什么条件时,s是有理数?
(2)当a,b,c,d满足什么条件时,s是无理数?
老鼠尾巴:a,b,c,d都是有理数,x是无理数.要使s容易判定,就要把s化为只含有一个x(无理数)的形式.

为“有理数+有理数÷(cx+d)”形式,从而
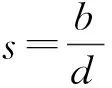

4 似“BD2=AB2+BC2,AP2+BQ2=PQ2”的结论是一种“老鼠尾巴”
这样的结论己暗示:要去构造出一个直角三角形,利用勾股定理来证明.
例4
如图3,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=CD,求证:BD2=AB2+BC2.
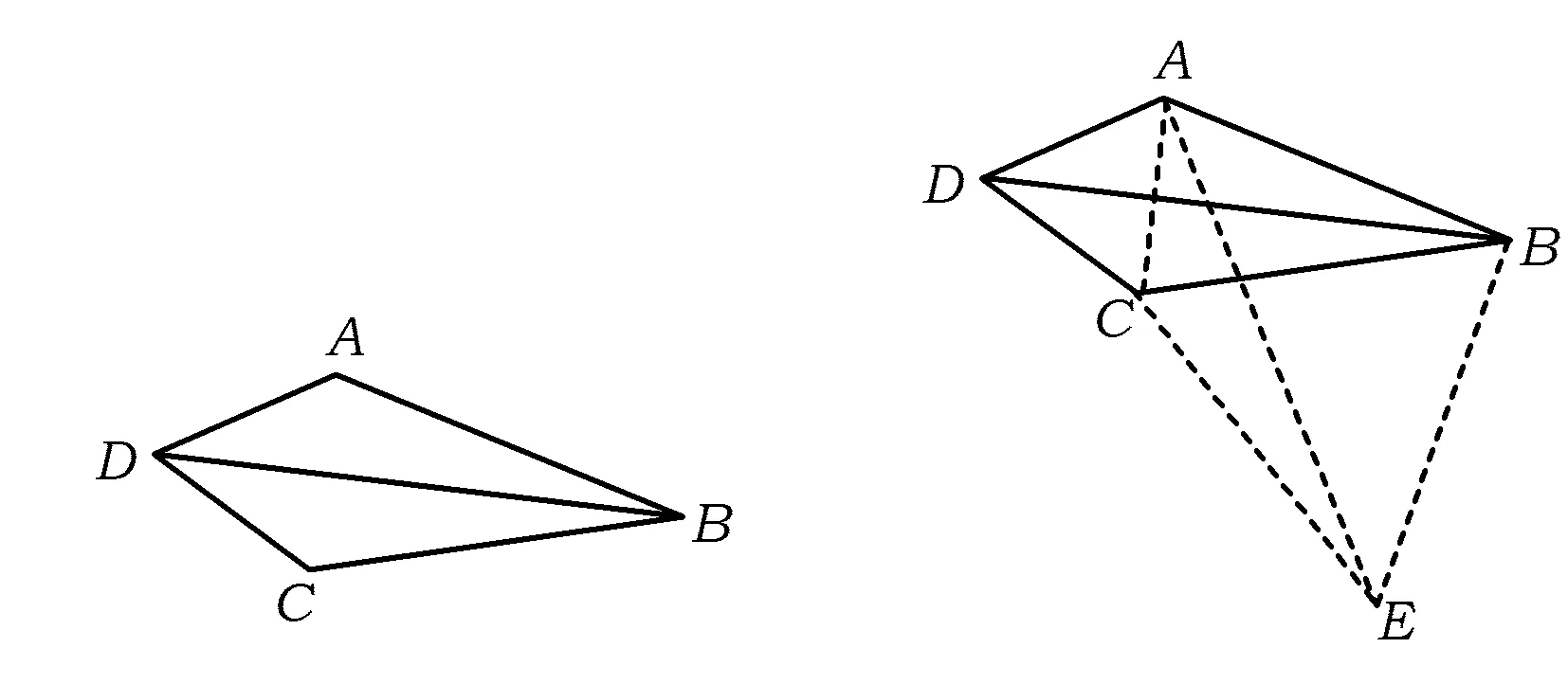
图3 图4
老鼠尾巴:BD2=AB2+BC2暗示要构造出一个以BD长为斜边的直角三角形.BD2=AB2+BC2与∠ABC=30°都是老鼠尾巴.
分析
由BD2=AB2+BC2知:要找到一个边长分别为AB,BC,BD的直角三角形.由∠ABC=30°知:30°+60°=90°,在边BC外作一个等边三角形,正好形成Rt△ABE,这时只要证AE=BD就可以了.
如图4,以BC为一边,向外作一个等边△BCE.联结AE,AC,则△ABE为直角三角形,且AB2+BC2=AB2+BE2=AE2.以下只要证明△DCB≌△ACE,从而DB=AE.
5 特殊数据是一种“老鼠尾巴”
像“∠ABD+∠BDC=90°”的条件,90°是特殊数据,也就是一条“老鼠尾巴”.
例5
如图5,在四边形ABCD中,AB=30,BC=14,CD=40,AD=48,∠ABD+∠BDC=90°,求四边形ABCD的面积.
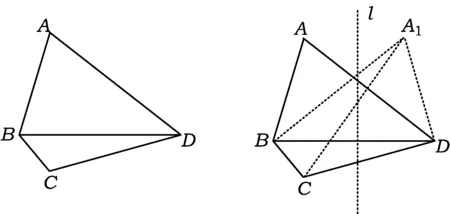
图5 图6
老鼠尾巴:∠ABD+∠BDC=90°是一条“老鼠尾巴”.
分析
作BD的中垂线l,把△ABD绕l翻折到△A1DB的对称位置,使得∠A1DC=∠A1DB+∠BDC=∠ABD+∠BDC=90°.这时,△A1DC为直角三角形,CD=40,A1D=30,∠A1DC=90°,从而A1C=50.而在△A1BC中,BC=14,A1B=AD=48,A1C=50,BC,A1B,A1C满足勾股定理,故∠A1BC=90°.于是
6 由不等式反映的范围是一种“老鼠尾巴”
不等式反映的范围,往往可以放缩、变换.己经有某种信息暗示于你了,因此它也是一种“老鼠尾巴”.
例6
求正整数对(a,b),同时满足条件:
老鼠尾巴:a,b为正整数,要满足2个不等式,问题便归结为:能否进行变形,先确定出某一个字母(a或b)的具体取值范围.
分析1

从而
a>1.
由条件(1)可知
结合条件(2),得
于是
2a-1<6,
即
a≤3,
故
1 当a=2,b=1时,不满足条件(2);当a=3,b=2时,正好满足2个条件,这便是本题的答案. 分析2 因为53<150<200<63,所以 b≥1,a≥2. 从而 b<3, 于是1≤b<3.以下分b=1,b=2讨论即可. 分析3 5<2a<7, 从而2≤a≤3.以下对a=2,a=3进行讨论即可. 从而只能b=2.以下再验证a的值即可. 问题中的特异条件,有时恰恰是可以利用的“老鼠尾巴”. 图7 例7 分析 2∠ADB+∠BDC=180°. 利用它来添辅助线:延长CD到E,∠CDE正好是一个平角∠ADB+∠BDC+∠ADE=180°,从而 ∠ADB=∠ADE, 再在CE上取DE=DB,这时△ADB≌△ADE.接着,AE=AB=AC,从而 ∠AED=∠ABD=60°=∠ACD, 从而△ACE是等边三角形,于是 AB=AC=CE=DE+CD=BD+DC. 评注 特别注意:本解很自然地从“老鼠尾巴”推出添辅助线的方法.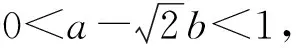



7 “特异条件”是一种“老鼠尾巴”