对一道解析几何模考题的探究

●

(北仑中学 浙江宁波 315800)

题目

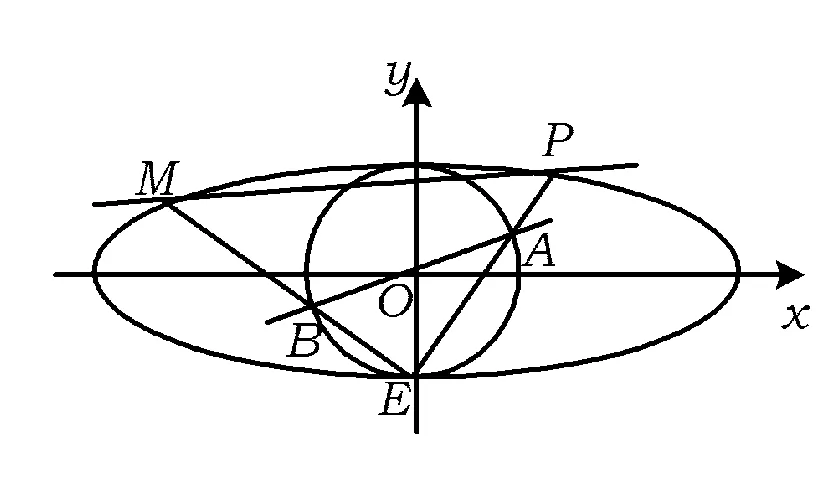
图1

(1)求椭圆C1的标准方程.

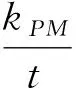
②求△EPM面积最大时直线l的方程.

(2014年宁波市高三十校联考数学模拟试题理科第21题)

这是一道设计新颖、知识面覆盖广、综合性极强的解析几何题.作为联考模拟试题,它具有良好的区分度，并且与近几年浙江省高考解析几何综合题考查圆和圆锥曲线以及多条直线的命题思路十分贴切，是一道值得深入学习和探究的好题目.特别是第①小题，本文对它进行命题推广进而获得更一般的结论.

命题1

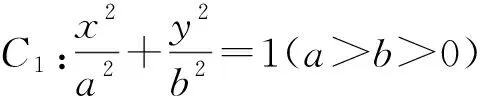
证明

不妨设直线EA的斜率为k,设A(x1,y1)，B(x2,y2),P(x3,y3),M(x4,y4).先联立直线EA与圆的方程得

从而

(k2+1)x2-2kbx=0，

解得

因此

(a2k2+b2)x2-2kba2x=0,

从而

于是

故

命题1表明直线MP的斜率与直线AB的斜率比值是一个只跟离心率有关的定值.若将圆的方程改为x2+y2=a2,并且将下顶点改为左顶点，则有类似结论成立.

命题2

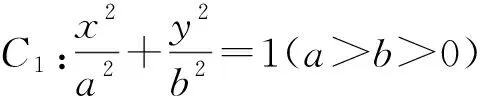
命题2的证明与命题1类似.事实上,在命题1的条件下除了定值外还能发现定点.

命题3

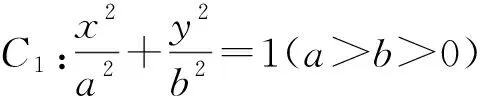
证明

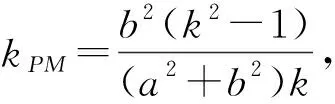
即

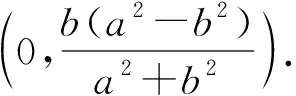
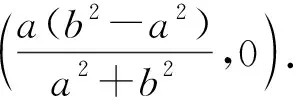
若将命题1所涉及的椭圆情形推广到双曲线和抛物线，则可以得到下列2个命题：

命题4

证明

设直线EA的方程为x=my-a,设A(x1,y1),B(x2,y2),P(x3,y3),M(x4,y4).联立圆与直线方程得

从而

(m2+1)y2-2amy=0,

解得

于是

将坐标代入,得

再联立双曲线方程和直线方程得

从而

(b2m2-a2)y2-2amb2y=0，

解得

则

故

接着写出直线MP的点斜式方程，得

化简得

将以上情况进一步推广到抛物线，下面只以开口向右的抛物线为例进行说明，其余情况类似.

命题5

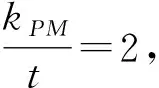
说明

(1)命题5中直线OA,OB之一有可能与开口较开阔的抛物线没有交点，因此这个结论需要在点M,P都存在的前提下成立.

(2)命题5的证明可以参照命题1进行.

从推广过程可以看到，上述结论揭示了圆锥曲线中普遍存在的一个定值和定点结论.在高考复习中，教师应当站得高、看得远，精心挑选好的例题和练习，不仅讲题目，讲技巧，讲思路，而且要讲方法，讲思想，讲拓展，高屋建瓴地看待数学高考复习背景下知识内在的联系，而不能疲于题海训练.