一种导管架钢桩跨距精确测量的新方法

张士舰 刘春杰 肖立权 李小红 孟令河 宋国辉

(海洋石油工程股份有限公司)

一种导管架钢桩跨距精确测量的新方法

张士舰 刘春杰 肖立权 李小红 孟令河 宋国辉

(海洋石油工程股份有限公司)

提出了一种导管架钢桩跨距精确测量的新方法,即利用绕向量旋转坐标变换方法使空间圆与平面圆能够相互转换、运用最小二乘法计算钢柱圆心三维坐标、使更多的观测值参与圆心计算,克服了传统方法测量精度较低的缺点,消弱了钢桩椭圆度造成的误差影响,大大降低了海上组块安装的风险,对海上安装施工具有重要指导意义。本文提出的这一数学计算原理可以推广到任何圆柱型杆件构成的钢结构圆心定位测量,应用范围非常广。

导管架;过渡段;最小二乘法;绕向量旋转;圆心坐标;钢桩跨距;测量

海洋石油平台的组块一般通过桩顶过渡段安装在导管架上,过渡段之间的跨距由桩顶切割位置确定,所以精确测量并准确控制钢桩跨距至关重要,它关系到平台与过渡段能否准确对接[1-2]。传统测量钢桩跨距的方法一般是利用全站仪测量钢桩截面圆3点坐标的方法计算圆心坐标[3],或测量钢桩的母线位置坐标[4],这2种方法虽快捷,但因钢桩存在椭圆度,计算的圆心坐标精度较低,导致最终计算的跨距精度也较低。本文提出了一种新方法,即利用全站仪测量钢桩正截面若干点(一般多于6个点)的三维坐标,再利用坐标变换法与最小二乘法精确计算各个钢桩圆心坐标,这样可以最大程度地减小因钢桩椭圆度造成的误差,进而精确计算出各个钢桩之间的跨距,从而准确指导钢桩切割位置的调整。

1 钢桩圆心坐标的计算

钢桩可分为单倾、双倾、无倾度等形式,其中无倾度形式最简单,在此不作说明。以BZ34-1 WHPD导管架为例计算钢桩的圆心坐标(图1),该导管架B1与B2导管为单倾1∶10,A1与A2为双倾1∶7.07,导管架顶部(皇冠板底部)标高为EL(+)7 000mm,钢桩理论切割线的标高为EL(+)7 750mm。首先,沿着钢桩方向用钢卷尺从导管顶部(皇冠板根部)量取理论数值;再按照文献[5]方法,根据倾度计算结果(即B1与B2的理论切割线距离导管顶部为753.7mm,A1与A2的理论切割线距离导管顶部为757.5mm)找到各个钢桩理论切割位置后,用一长方形围板在钢桩理论切割线处找到一正截面,如图2所示;最后将全站仪架设于一合适位置,可以通视各个钢桩,测量钢桩正截面上n个点坐标(xi,yi,zi)(i=1,2,…,n)。

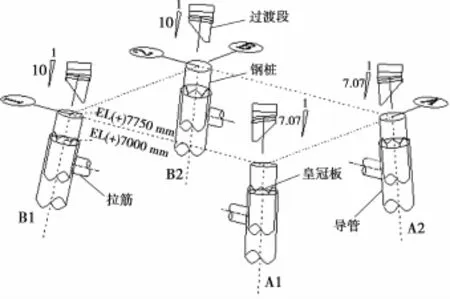
图1 BZ34-1WHPD海上导管架钢桩及过渡段示意图

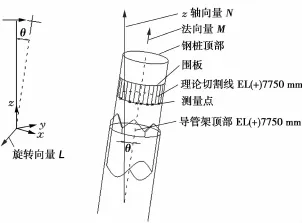
图2 BZ34-1WHPD海上导管架钢桩测量示意图

因为钢桩正截面是倾斜的,所以为了准确计算圆心坐标,首先依据正截面的法向量进行坐标转换,把倾斜的圆转换为平面圆,以便完成圆心计算。

设正截面的方程为z=ax+by+c,运用最小二乘法[6-7]计算a、b、c这3个待求参数,即

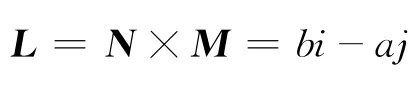
其单位向量为

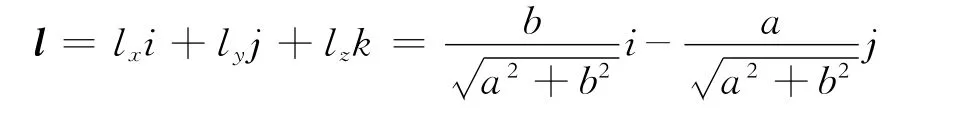
设绕l旋转后的测量点集为(x′i,y′i,z′i),i= 1,2,…,n,则测量点集绕单位向量l旋转的公式为

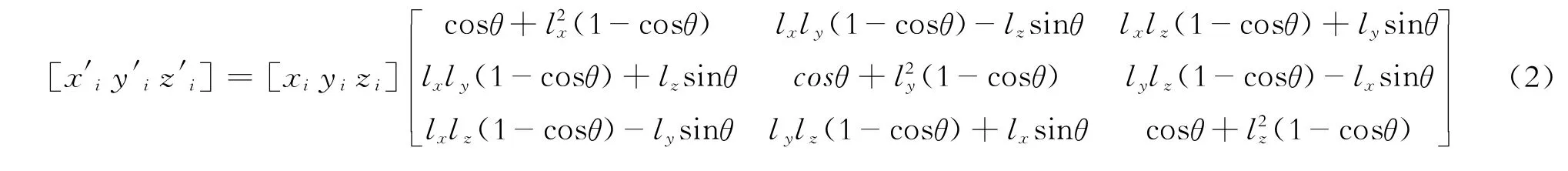
至此,由原始测量点构成的空间圆转换为平面圆。

为更准确地计算圆心坐标,依旧利用最小二乘法计算圆参数。如图3所示,旋转后最小二乘圆面的法线已经处于垂直状态,最佳面的高程(Z值)为。设圆方程为x2+y2+dx+ey+f= 0,运用最小二乘法计算d、e、f这3个待求参数,即

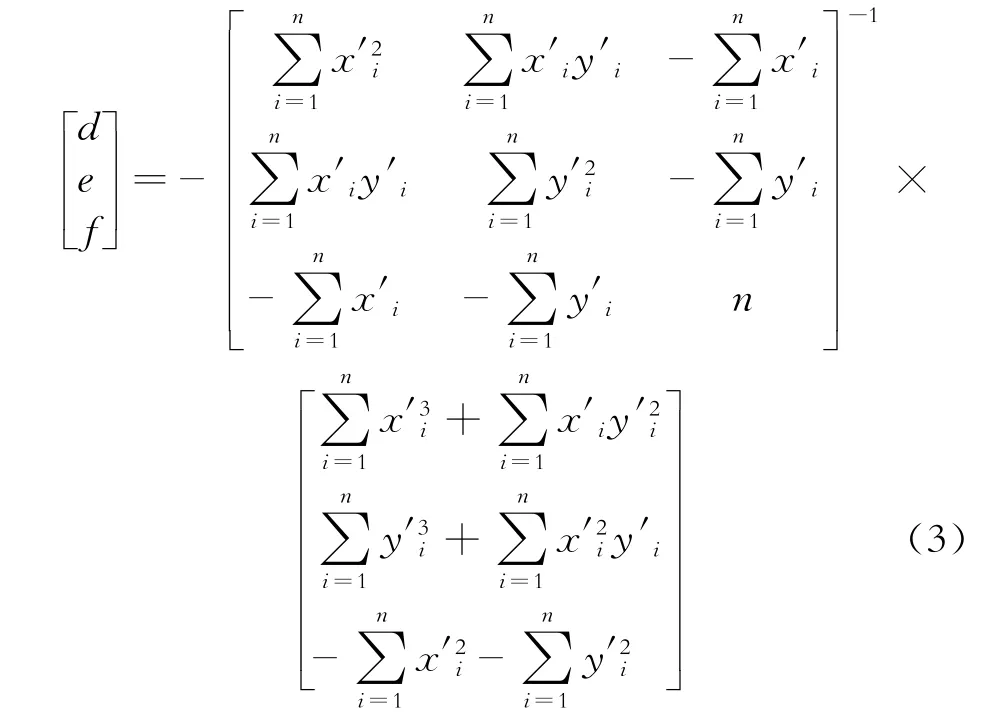
圆方程变换为圆心表达式为

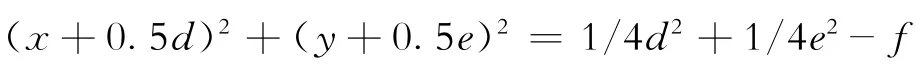
最佳圆心坐标为

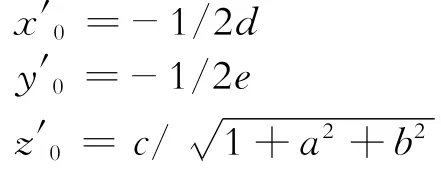
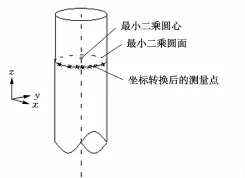
图3 BZ34-1WHPD海上导管架钢桩圆心计算示意图

至此,圆心坐标虽已经计算完毕,但这个圆心坐标是原始坐标绕向量L旋转θ角度后计算的圆心,并非原始状态下的圆心坐标,所以需要把圆心坐标绕向量L反向旋转θ角度,这样才得空间圆心坐标。设最终状态的圆心坐标为(x0,y0,z0),其计算公式为

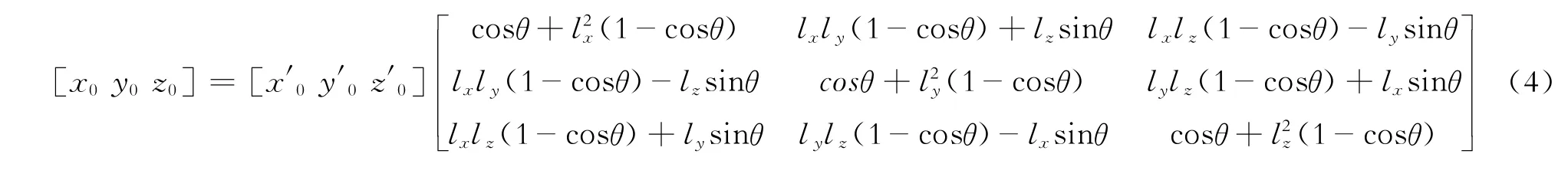
如图4所示,反向旋转θ角度后,最佳面的法向量又回到初始状态。至此,圆心的空间坐标已经计算完毕,通过两点间距离计算公式就可以计算各个钢桩的跨距了。

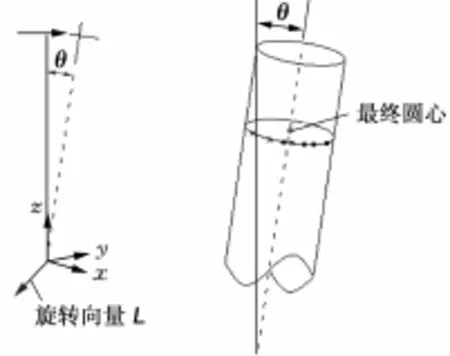
图4 导管架钢桩圆心反转示意图

2 精度评定

利用最小二乘法计算圆心坐标比传统方法精度高[7],其圆心点位精度评定方法如下:根据本文推导的公式(3)可以计算出最佳圆方程的3个参数d、e、f,进而可以计算出所有测量点与最佳圆周的偏差值的平方和φ。设圆方程3个参数的协因数阵为,则由式(3)可知

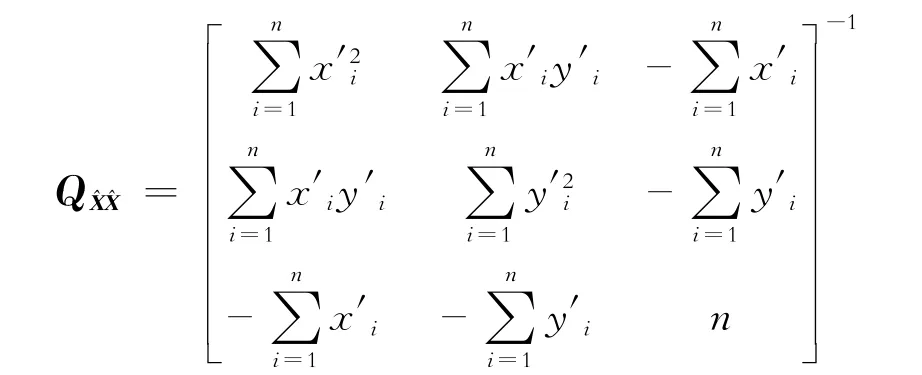
3 实际运用

3.1 计算程序编写

根据上述圆心坐标计算的数学原理,利用AUTOCAD VBA编写计算程序。之所以选择AUTOCAD VBA编写圆心坐标计算程序,是因为VBA语言比其他计算机语言编写独立应用程序更具优越性,它可以省略数据的输入,用鼠标点击各个测量点代替了数据的输入,并且能够在AUTOCAD中直接生成图形,操作非常方便,执行效率非常高。全站仪测量数据完毕后,其存储卡可以直接插入计算机的USB口,直接用AUTOCAD打开DXF测量数据文件,调用VBA编写的圆心坐标计算程序就可以在AUTOCAD窗口中直接生成圆心点。

3.2 实测数据分析对比

以BZ34-1WHPD导管架钢桩海上测量数据为例,测量的全站仪为徕卡1201,其测角精度为1s,测距精度为1mm+1.5mm(每1 km增加1.5mm误差),测量数据与计算结果如表1所示。从表1可知,圆心点位中误差都在3mm左右,足以满足钢结构建造与安装的精度(圆心点位中误差值越小,说明桩的圆度越好),其中A1桩腿的圆心点位中误差最小,所以其圆度比其他3个桩的圆度好些。

传统方法是在圆周上测量3点的三维坐标,运用三点定圆的计算方法计算圆心坐标。为分析对比传统方法与本文方法的精度,以A1桩腿为例,选择多组分散的三点分别计算圆心坐标,选择的点号组合分别为(P 1,P 3,P 5)、(P 1,P 3,P 6)、(P 1,P 3,P 7)、(P1,P4,P7)、(P1,P4,P6)、(P1,P5,P7)、(P2,P4, P6)、(P2,P4,P7)、(P2,P5,P7)、(P3,P5,P7),计算出的这10组圆心坐标与本文提出的最小二乘法计算的圆心坐标位置对比如图5所示。

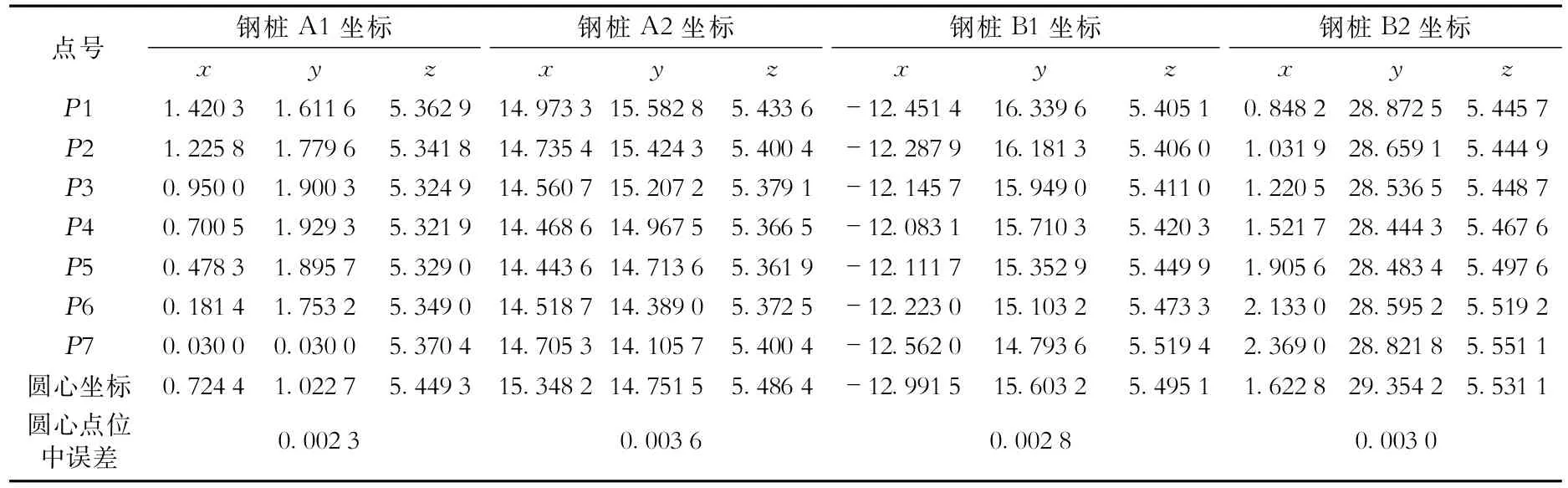
表1 BZ34-1WHPD导管架钢桩测量数据及计算结果 m

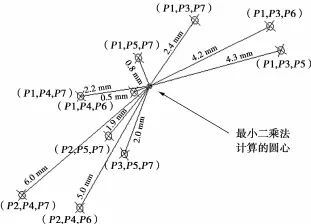
图5 传统的三点定圆法与本文提出的最小二乘法计算得到的导管架钢桩圆心位置分布图(以BZ34-1WHPD导管架A1桩腿为例)

从图5可以看到,运用传统的三点定圆法计算的多组圆心分散在最小二乘圆心周围。由于受椭圆度的影响,三点定圆法测量点少,圆心坐标精度较低,而最小二乘法通过测量更多观测值,而且更多测量点参与计算,消弱了椭圆度造成的误差影响,圆心坐标精度更高。在实际运用中,圆周的测量点数越多,则圆心精度越高,一般海上测量钢桩的测量点数取6～10个。根据表1的圆心坐标计算的BZ34-1WHPD导管架各个钢桩的跨距如表2所示,据此可以得出各个钢桩实测跨距值与理论值的差值以及各个钢桩的倾度,进而对钢桩切割线进行上移或下移调整,以靠近理论跨距值。

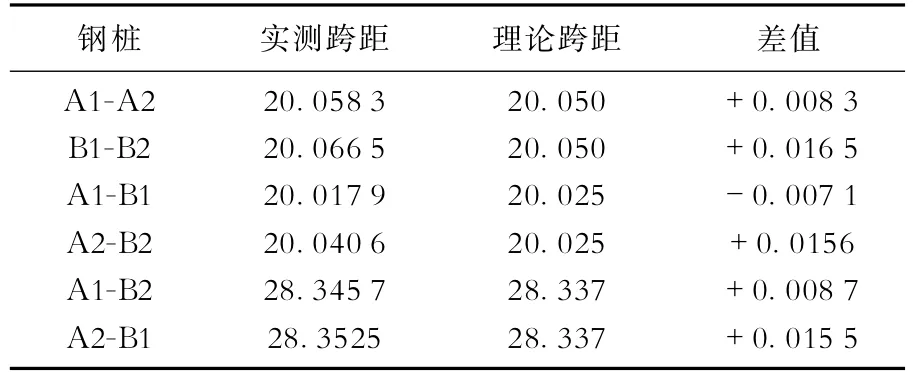
表2 BZ34-1WHPD导管架各个钢桩之间的跨距m

4 结论

1)运用最小二乘法计算钢桩圆心三维坐标,使更多的观测值参与圆心计算中,克服了传统方法测量精度较低的缺点,消弱了钢桩椭圆度造成的误差影响,显著提升了钢桩间跨距的测量精度与施工效率,大大降低了海上组块的安装风险。

2)利用绕向量旋转的坐标变换方法使空间圆与平面圆能够相互转换,可以计算任意倾斜度的钢桩圆心坐标,应用精度分析理论,计算出圆心点位中误差,可以非常直观地反映出钢桩的椭圆度情况。这一数学计算原理也可以推广到任何圆柱型杆件构成的钢结构圆心定位测量,应用范围非常广。

[1]张光明.平台组块过渡段设计中的若干问题及解决方法[J].中国海上油气(工程),1999,11(2):7-8.

[2]纪延涛,李军.滩海固定平台钢结构安装质量及精度控制[J].中国海洋平台,2005,20(2):45-51.

[3]张振山,米军,方向利.导管架钢桩测距及切割定位方法研究[J].海洋工程,2011,29(3):112-116.

[4]魏熊标,高瑞力.海洋固定平台过渡段安装技术分析[J].中国造船,2007,48(11):92-97.

[5]杨文友,高国鑫,徐少华,等.海洋固定平台过渡段安装技术的改进[J].中国造船,2009,50(11):107-113.

[6]刘春杰,张士舰,孙云虎.三维坐标系下检测导管架圆形杆件空间位置状态的方法:中国,ZL201010115279.X[P].2012-11-28.

[7]陶本藻,邱卫宁,黄加纳.误差理论与测量平差基础[M].武汉:武汉大学出版社,2003:102-148.

A newmethod for accuratemeasurement ofspans among jacketpiles

Zhang Shijian Liu Chunjie Xiao Liquan Li Xiaohong Meng Linghe Song Guohui
(China Offshore Oil Engineering Co.Ltd.,Tianjin,300452)

A newmethod for highprecisionmeasurement ofspans between jacketpiles is introduced in thispaper.Coordinates transformation by rotating around the vector and leastsquaremethod are included in themethod.Due tomoremeasuringpoints are involved to calculate the center of circle,the weakness of traditional lowprecisionmethod is conquered.As the error caused by roundness is weakened,the risk of installingmodule offshore is lowered.Thismethod issignificant for installation offshore.In addition,themathematical calculating theory in thispaper can extend to calculating the center of circle of cylinderstructure.So thismethod can be used inmany relevant fields.

jacket;transitionpiece;leastsquaremethod;rotate around vector;coordinate of circle center;span ofpiles;measurement

2013-09-24改回日期:2014-01-14

(编辑:叶秋敏)

张士舰,男,工程师,2004年毕业于西安石油大学测控技术与仪器专业,现主要从事钢结构测量技术研究工作。地址:天津市滨海新区渤海石油路688号595信箱海油工程检验公司(邮编:300452)。