一维复Ginzburg-Landau方程的分岔及其精确行波解

蔡 萍,唐驾时

(1.闽南师范大学数学与统计学院,福建 漳州 363000;2.湖南大学机械与运载工程学院,湖南 长沙 410082)

本文考虑如下一维复Ginzburg-Landau(CGL)方程:

ut=u+(1+iα)uxx-(1+iβ)|u|2u=0，

(1)

其中,u(x,t)是一复值函数,α,β是实参数.GL方程有着丰富的物理背景,在超导、相变、非平衡流体的调制不稳定性的偏微分方程,以及激光、化学反应的湍流问题的等离子体物理等方面有着广泛的应用,也是众多学者的研究对象.关于GL方程的丰富动力学行为已经有所研究,如新行波解[12],同宿轨解[13]及分岔[14].本文的目标是利用动力系统分支理论,研究方程(1)的分岔,获得其所有类型的精确行波解,并用椭圆函数和双曲函数来表示[15].本文不仅在推导上比文献[12]简单,解的表示形式也比文献[12]简洁.

1 CGL方程的分岔及相图

假设方程(1)具有如下形式的解:

u(x,t)=φ(ξ)ei(kx-ωt),ξ=x-ct，

(2)

其中,φ(·)是实函数,c,k,ω是实数.

把式(2)代入方程(1),分离实部和虚部,则有:

φ″+(c-2kα)φ′+(1-k2)φ-φ3=0,

(3)

αφ″+2kφ′+(ω-αk2)φ-βφ3=0.

(4)

由式(3)、(4)得

φ″-d0φ-2d1φ3=0，

(5)

其中,

方程(5)等价于如下二维平面动力系统:

(6)

对系统(6)首次积分:

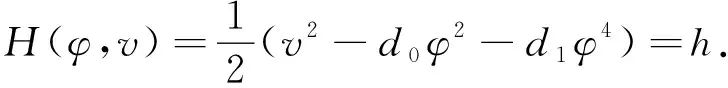
(7)

由向量场(6)定义的相轨道决定了方程(1)的行波解,并且系统(6)的同宿到一个奇点的同宿轨道对应方程(1)的孤立波解；连接两个奇点的异宿轨道对应方程(1)的扭波解或反扭波解；周期轨道对应方程(1)的周期波解.下面主要考虑系统(6)的有界解,因为只有有界解在实际物理模型中才有意义.

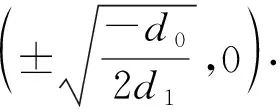
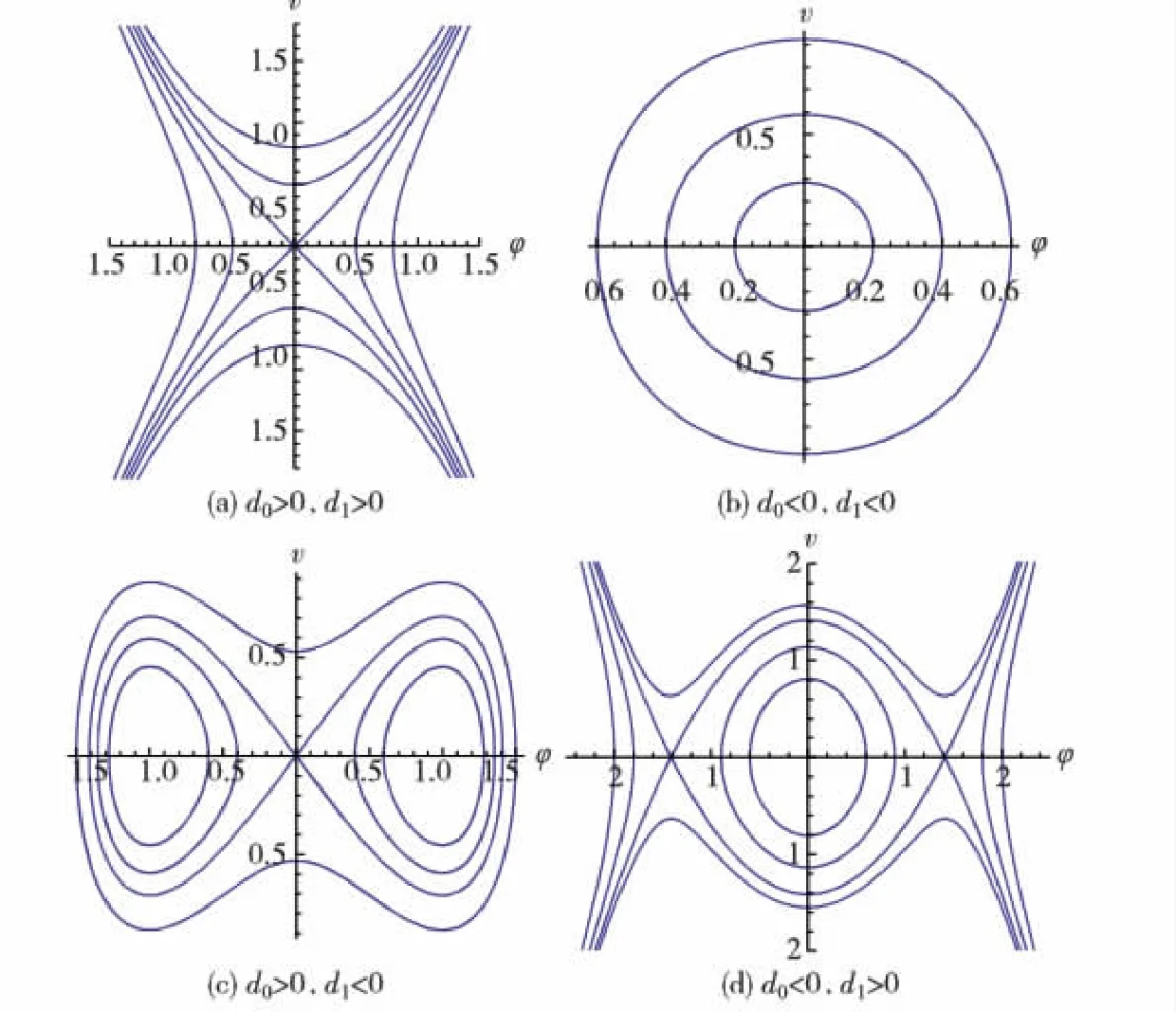
图1 系统(6)的分岔相图Fig.1 The bifurcation of phase portraits of system (6)

2 CGL方程的精确行波解

本节利用系统(6)的第1个方程和首次积分(7),获得方程(1)的精确行波解.

当d0<0,d1<0时,系统(6)只有一个平衡点(0,0),且为中心,如图1(b)所示.

对应于由H(φ,v)=h,h∈(0,∞)所定义的曲线,系统(6)存在无穷多的周期轨道,由式(7)得:

其中

由系统(6)的第一个方程得:

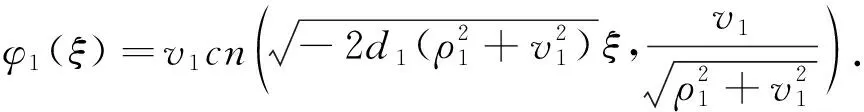
(8)

因此,方程(1)的一族周期波解为:

u1(x,t)=φ1(x-ct)ei(kx-ωt).

(9)

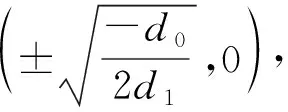
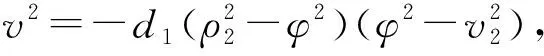
由系统(6)的第一个方程得:

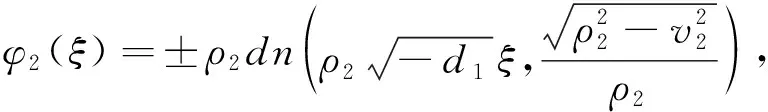
(10)

因此,方程(1)的两族周期波解为:

u2(x,t)=φ2(x-ct)ei(kx-ωt).

(11)

(ii) 对应于由H(φ,v)=h,h=0所定义的曲线,系统(6)存在过(0,0)的两条同宿轨道.由式(7)得:

由系统(6)的第一个方程得:

(12)

因此,方程(1)的两条孤波解为:

u3(x,t)=φ3(x-ct)ei(kx-ωt).

(13)

(iii) 对应于由H(φ,v)=h,h∈(0,∞)所定义的曲线,系统(6)存在一族周期轨道,对应系统(1)的一族周期波解同式(9).

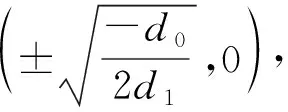
由系统(6)的第一个方程得:

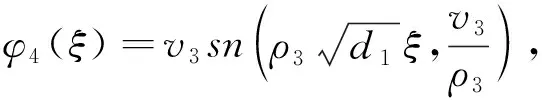
(14)

因此,方程(1)的一族周期波解为:

u4(x,t)=φ4(x-ct)ei(kx-ωt).

(15)

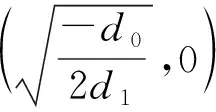
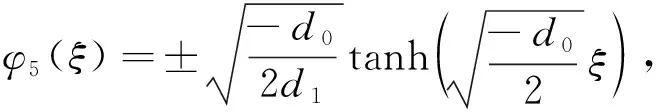
(16)

因此,方程(1)的扭波解和反扭波解为:

u5(x,t)=φ5(x-ct)ei(kx-ωt).

(17)

3 结 论

通过行波变换,把CGL方程转化为平面动力系统,借助动力系统的分岔理论,利用连接平衡点的闭轨线的特点,结合轨线与行波之间的关系,给出了CGL方程的所有分岔相图,并得到了其所有类型的有界行波解.据作者所知,对于CGL 方程,相关的定性分析并没有文献给出.由此可以看出,动力系统方法是研究非线性演化方程行波解的有效方法.

[1] Layeni O P,Akinola A P.A new hyperbolic auxiliary function method and exact solutions of the mBBM equation[J].Commun Nonlinear Sci Numer Simulat,2010,15:133-138.

[2] Feng J S,Li W J,Wan Q L.Using (G′/G)-expansion method to seek the traveling wave solution of Kolmogorov-Petrovskii-Piskunov equation[J].Applied Mathematics and Computation,2011,217(12):5860-5865.

[3] AbdelRady A S,Osman E S,Mohammed K.The homogeneous balance method and its application to the Benjamin-Bona-Mahoney equation[J].Applied Mathematics and Computation,2010,217(4):1385-1390.

[4] Wazwaz A M.A sine-cosine method for handling nonlinear wave equations[J].Mathematical and Computer Modelling,2004,40 (5/6):499-508.

[5] 刘式达,刘式适,叶其孝.非线性演化方程的显式行波解[J].数学的实践与认识,1998,28 (4):289-301.

[6] 刘式达,刘式适.孤立波与同宿轨道[J].力学与实践,1991,13(4):9-15.

[7] Xie S L,Wang L,Zhang Y Z.Explicit and implicit solutions of a generalized Camassa-Holm Kadomtsev-Petviashvili equation[J].Commun Nonlinear Sci Numer Simulat,2012,17:1130-1141.

[8] Yan F,Hua C C,Liu H H.Bifurcation of phase and exact traveling wave solutions of a higher-order nonlinear schrödinger equation[J].International Journal of Bifurcation and Chaos,2012,22(5):1250121.

[9] Deng S F,Sheng F,Guo B L,et al.Travelling wave solutions of a generalized Camassa-Holm-Degasperis-Procesi equation[J].Science China Mathematics,2011,54 (3):555-572.

[10] Wen Z S,Liu Z R.Bifurcation of peakons and periodic cusp waves for the generalization of the Camassa-Holm equation[J].Nonlinear Analysis:Real World Applications,2011,12:1698-1707.

[11] Cai J H,Qiu W,Jia P Z.Exact traveling wave solutions for a modified Camassa-Holm equation[J].Applied Mathematics and Computation,2010,217:607-611.

[12] 邱春,贾多杰,高秀云,等.复Ginzburg-Landau方程的新行波解[J].西北师范大学学报:自然科学版,2008,44 (1):38-42.

[13] Dai Z,Li Z,Liu Z,et al.Exact homoclinic wave and soliton solutions for the 2D Ginzburg-Landau equation[J].Physica Letters A,2008,372 (17):3010-3014.

[14] Norimichi H,Sawomir R.A remark on global bifurcations of solutions of Ginzburg-Landau equation[J].Nonlinear Analysis:Real World Applications,2011,12:2943-2946.

[15] Prasoolov V,Solovyev Y.Elliptic functions and elliptic integrals[M].New York:Amer Math Soc,1997.