一类波动方程的全离散H1-Galerkin混合有限元方法
2014-08-06于顺霞
于顺霞
(潍坊科技学院机械系,山东寿光267000)
讨论如下二阶双曲型方程初边值问题:
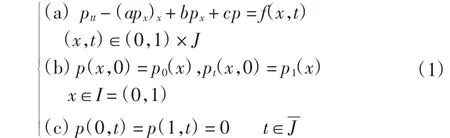
现代科学技术工程中的大量数学模型都可用偏微分方程来描述,双曲型偏微分方程是描述振动或波动现象的一类重要的偏微分方程.关于这类方程有限元方法的研究已有一些结果[1-6].文献[1-2]研究了非线性双曲型方程的全离散有限元方法的稳定性和收敛性估计,这些研究成果都为以后的工作打下了重要基础.文献[3]和文献[4]分别讨论了一维和高维双曲型方程的H1-Galerkin混合有限元方法的三层全离散格式,得到了最优误差估计.本文给出二阶双曲型方程的H1-Galerkin混合有限元方法的二层全离散格式,并进行误差分析,得到了最优阶误差估计.本文中C、ε分别表示普通常数和一个普通小正数,不同式中的C、ε可能不同.
1 格式的建立
令 apx=u,ut=q,α(x)=1/a(x),β(x)= α(x)·b(x),将 apx=u 与 vx做内积,并由 α(x)=1/a(x)得式(2)(a).将式(1)(a)与 wx做内积,利用分部积分和边界条件pt(0)=pt(1)=0得式(2)(b).于是与问题(1)等价的变分形式为:求满足
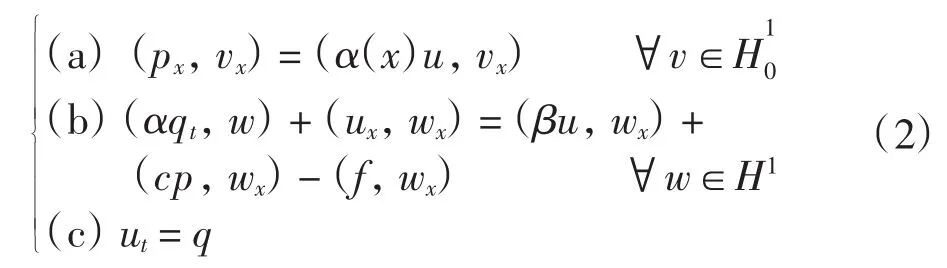
令Vh和Wh分别是和H1的有限维子空间,有如下逼近性质:对于1≤p≤∞和k>0,r>0的整数,满足
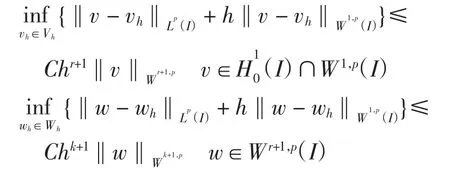
问题(2)的半离散H1-Galerkin混合有限元方法为:求{ph,uh,qh}∈Vh× Wh× Wh,满足
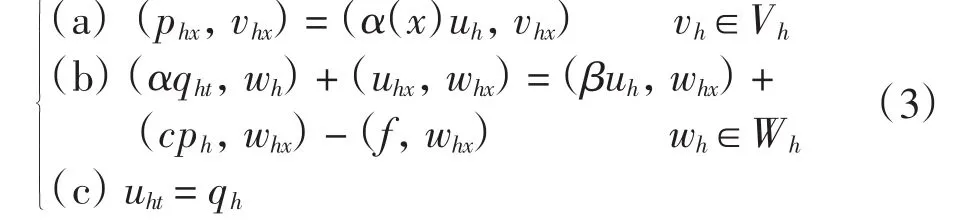
其中uh(0)和qh(0)分别为u0(x)=ap0x(x),q0(x)=ap1x(x)的某种近似.这3个方程构成了微分代数方程,因为刚度矩阵是正定的,因此问题(3)对于给定初值是唯一可解的.
由文献[7],定义椭圆投影{uh,ph}:[0,T]→Wh×Vh为
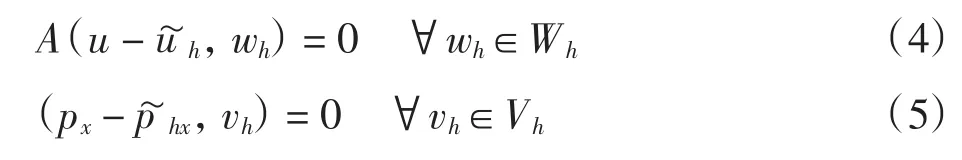
其中 A(u,v)=(ux,vx)-(βu,vx)+ λ(u,v),这里选取 λ 使 A(·,·)是 H1-正定的,即存在常数 α0> 0,使得且容易证明 A(·,·)是有界的.
下面对半离散问题(3)关于时间离散化,以导出全离散格式.取正整数N,时间步长为τ=T/N,tn=nτ(n=0,…,N),对于在 t=tn有定义的函数 v,记

将式(3)关于时间离散化,并将 uh、f在 tn-1,tn,tn+1的值做权平均,得全离散格式:求Wh,满足

上述格式的初值按下面的方式确定,
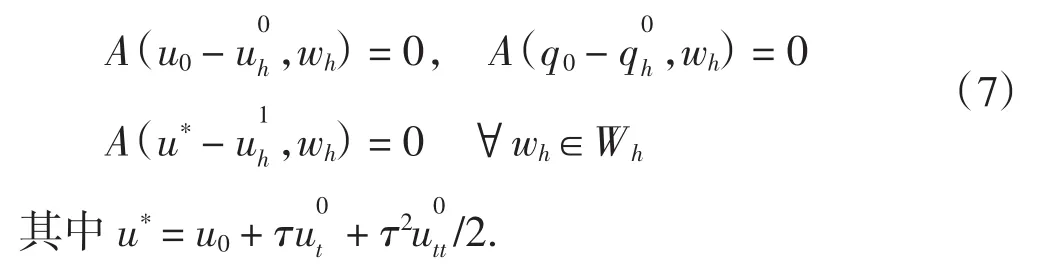
2 格式的误差估计
令ρ=u-uh,η=p-ph,对于ρ、η,由文献[7]可得估计


证明 ρ、η与e的估计已经由式(8)~式(11)给出,只需估计 ξ、ζ与 θ.在式(12)中取 vh= ζn+1/2,得
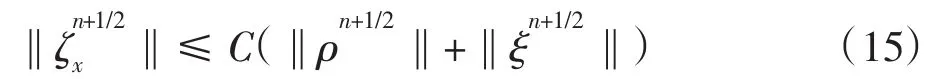
在误差方程(13)中取 wh==+ δn,其中
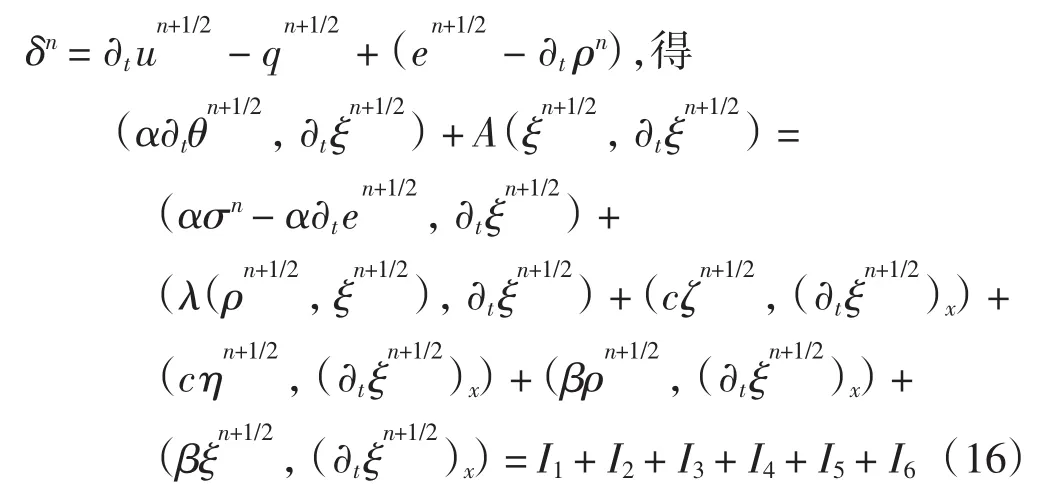
下面分别估计上式各项.对左端第1项,有

对上式右端第2项利用分部求和公式,有
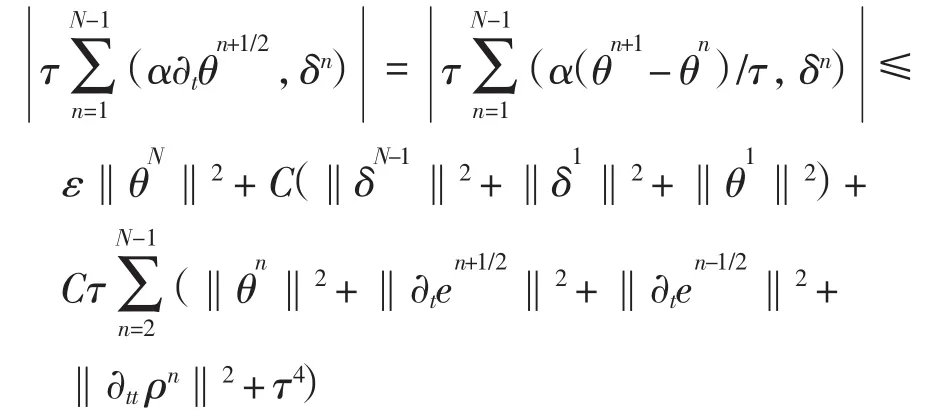
对式(16)左端第2项,有
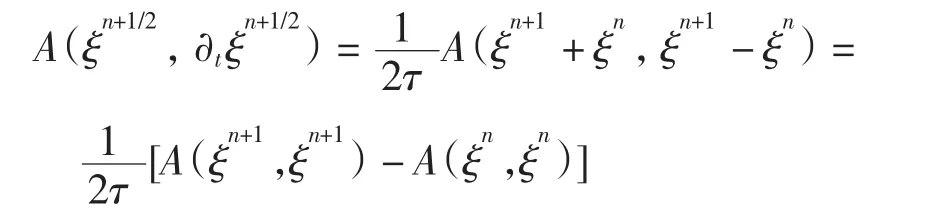
下面估计式(16)的右端各项.对|I1|和|I2|,利用柯西不等式,有

对|I3|,由格林公式及柯西不等式,并利用式(15),有
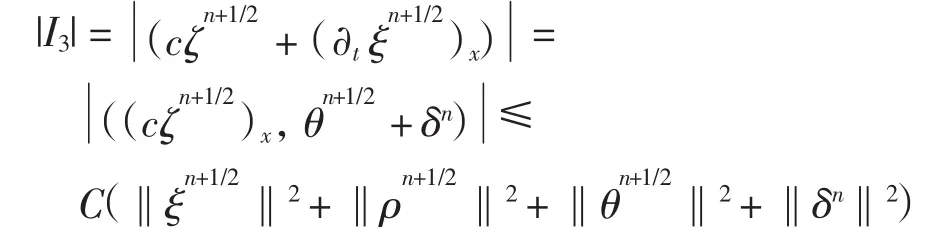
对I4,经整理并利用柯西不等式,有
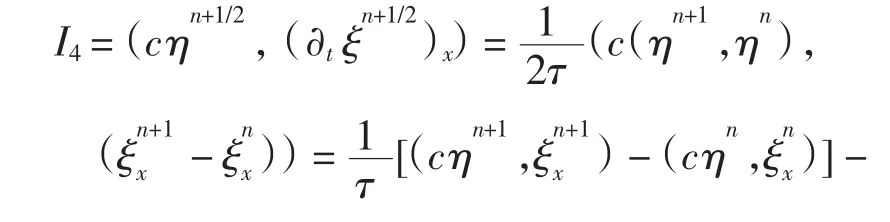

对I5和I6,与I4类似,有
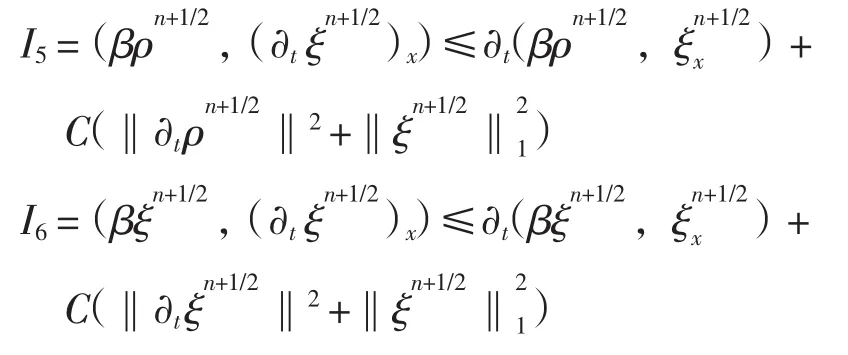
将上面各项估计代入式(16),两边同时乘以2τ,并关于n=1,2,…,N-1求和,注意到α的有界性,由A的正定性及有界性,利用ε-Cauchy不等式,有

当τ、ε充分小时,由Gronwall引理得

由u*的取法及泰勒展开式,可得
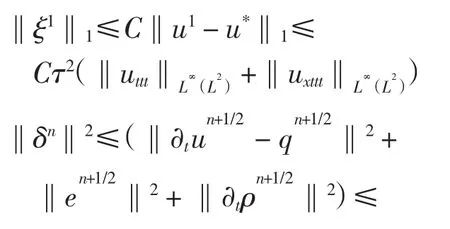

所以,由式(8)~式(11)得

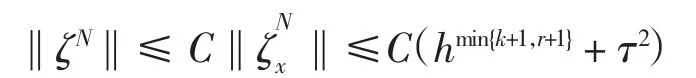
最后由三角不等式得结论成立.证毕.
[1]刘小华.关于一类二阶非线性双曲型方程的全离散有限元方法的稳定性和收敛性估计[J].高等学校计算数学学报,2002,25(1):15-22.
[2]王宏.关于非线性双曲型方程全离散有限元方法的稳定性和收敛性估计[J].计算数学,1987,9(2):163-175.
[3]于顺霞,杨青.双曲型方程全离散H1-Galerkin有限元方法[J].科学技术与工程,2007,7(1):18-21.
[4]杨青,于顺霞,李丽芳.高维双曲型方程全离散H1-Galerkin有限元方法[J].山东师范大学学报:自然科学版,2007,22(4):8-11.
[5]王瑞文.双曲型方程的混合元法[D].济南:山东师范大学,2004.
[6]甘小艇,张坤.抛物和双曲方程全离散间断有限体积元法[J].西北师范大学学报:自然科学版,2012,48(1):15-21.
[7]WHEELER M F.A priori L2-error estimates for Galerkin approximations to parabolic differential equation[J].SIAM J Numer Anal,1973,20(10):723-749.
