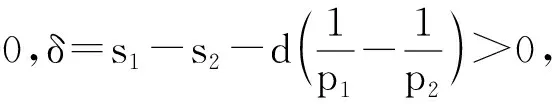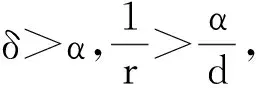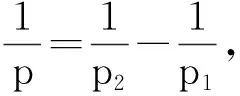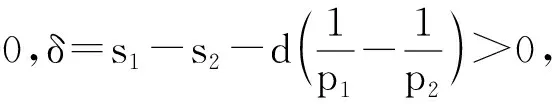加权Besov嵌入中的线性随机宽度*

王晶晶, 钱李新

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

令X,Y是赋范空间(或拟范空间),T是X|→Y的连续线性算子,用

Tn=φ∘N,N:X|→Rn,φ:Rn|→Y

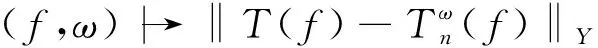
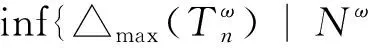
随着离散化技巧[3]的广泛应用,一些经典函数空间(如Besov空间)在一致框架下的各种经典宽度,如线性宽度、KoLmogorov宽度和GeLfand宽度等已经有了比较完整的结果[4].而对于Besov空间中的平均宽度、随机宽度和概率宽度的结果则不是很多[5-8].近年来,随着函数空间理论的进一步发展,开始在经典的函数空间中引入适当的权函数,并研究加权函数空间中的宽度问题,取得了一些成果,如加权Besov空间中的熵数、逼近数、GeLfand宽度和KoLmogorov宽度等[9-12].本文主要对加权Besov空间嵌入中的线性随机宽度的渐进阶进行了估计.

1 预备知识及引理

则可以定义如下的加权Besov空间:

其中,S′(Rd)表示所有定义在Rd空间内所有缓増广义函数的集合.

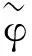
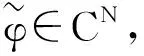
φj,k(x)=2jd/2φ(2jx-k),ψi, j,k(x)=2jd/2ψi(2jx-k).

其中: j∈N0:=N∪{0};k∈Zd.

由引理1知,当1≤p,q≤∞时,可以定义下面的加权序列空间:

Lq(2jsLp(α)):=

当p,q=∞时,取通常意义下的范数.

在加权Besov空间中有如下经典的嵌入定理:

定理1在加权序列空间中也成立.

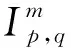
在有限维Lp空间中,Mathé[2,5]给出了相应线性随机宽度的渐进阶.

令0

(1)

2 主要结果

受引理3与文献[9]的启发,可以得到在加权序列空间中线性随机宽度的渐进阶.

其中:B1=Lq1(2jδLp1(α));B2=Lq2(Lp2).

证明 令Λ:={λ=(λj,k):λj,k∈C, j∈N0,k∈Zd},Ij,i⊂N0×Zd,使得

Ij,0:={(j,k):|k|≤2j},j∈N0;

(2)

Ij,i:={(j,k):2j+i-1<|k|≤2j+i},i∈N, j∈N0.

(3)

令Pj,i:Λ|→Λ是Ij,i内的标准投影算子,对任意的λ∈Λ,记

其中:u∈N0;v∈Zd;i≥0.则

Mj,i:=|Ij,i|～2d(j+i);

(4)

(5)

ωj,k=ωα(2-jk)～2iα,(j,k)∈Ij,i,i≥0.

(6)

根据线性随机宽度的基本性质[2],有

(7)

1)当1≤p1≤p2≤2时,先给出上方估计.对任意的r>0,由式(1)与式(7)得

(8)

对任意的M∈N0,令

(9)

对于1≤p1≤p2≤2,由引理3得

(10)

从而

(11)

因此,

(12)

由式(11)和式(12),令μ=min(δ,α),就有

(13)

考虑下方估计:由图表

及线性随机宽度的基本性质[2]得

(14)

式(14)中,S和T在不同的情形下由下面的定义给出.

(T(λ))i=λL,φ(i),1≤i≤N.

因此,由式(4)和式(6)可得

‖T‖=1,‖S‖≤c2Lδ.

(T(λ))i=λ0,φ(i),1≤i≤N.

因此,由式(4)和式(6)可得

‖T‖=1,‖S‖≤c2Lα.

(15)

再根据式(13)和式(15)可得

(16)

(17)

因此,只需将式(10)换作

再重复1)中的方法,就可得

(18)

3)当p1≤2≤p2< ∞时,只需将式(17)换作

(19)

即可证得

(20)

综上,由式(16)、式(18)和式(20),即可证得定理2.

注1当α=0,即μ=0时,定理2得到的结果与文献[2]中不加权序列空间的结果一致.

由引理1、定理1及离散化技巧,可以将加权序列空间得到的定理2自然地转化为加权Besov空间中的线性随机宽度,从而得到本文的主要结果:

注2当μ=δ时,定理3得到的结果与文献[6]中在Lipschitz有界域上得到的结果一致.

参考文献：

[1]Traub J F,WasiLkowski G W,Wozniakowski H.Information-Based compLexity[M].New York:Academic Press,1988.

[2]Mathé P.Random approximation of SoboLev embeddings[J].J CompLexity,1991,7(3):261-281.

[3]Maiorov V E.Discretization of the probLem of diameters[J].Uspekhi Mat Nauk,1975,30(6):179-180.

[4]Pinkus A.n-widths in approximation theory[M].New York:Springer,1985:234-247.

[5]Mathé P.Approximation theory of stochastic numericaL methods[M].BerLin:HabiLitationsschrift,Fachbereich Mathematik,Freie Universität,1994.

[6]Fang Gensun,Qian Lixin.Linear average and stochasticn-widths of Besov embeddings on Lipschitz domains[J].J Approx Theory,2009,161(1):9-22.

[7]Novak E.OptimaL Linear randomized methods of Linear operators in HiLbert spaces[J].J CompLexity,1992,8(1):22-36.

[8]Chen Guanggui,Fang Gensun.ProbabiListic and average widths of muLtivariate SoboLev spaces with mixed derivative equipped with the Gaussian measure[J].J CompLexity,2004,20(6):858-875.

[9]Kühn T,LeopoLd H G,SickeL W,et aL.Entropy numbers of embeddings of weighted Besov spaces[J].Constr Approx,2005,23(1):61-77.

[10]Kühn T,LeopoLd H G,SickeL W,et aL.Entropy numbers of SoboLev embeddings of radiaL Besov spaces[J].J Approx Theory,2003,121(2):244-268.

[11]Skrzypczak L.On approximation numbers of SoboLev embeddings of weighted function spaces[J].J Approx Theory,2005,136(1):91-107.

[12]Zhang Shun,Fang Gensun.GeLfand and KoLmogorov numbers of SoboLev embeddings of weighted function spaces[J].J CompLexity,2012,28(2):209-223.

[13]TriebeL H.Theory of function spaces[M].BaseL:Birkhäuser,1983：33-184.

[14]TriebeL H.Theory of function spaces II[M].BaseL:Birkhäuser,1992:87-139.

[15]Pietsch A.Operator IdeaLs[M].New York:North-HoLLand,1980:87-103.