Distance Spectral Radius of Bicyclic Graphs with Disjoint Cycles

Zhu Zhongxun, Luo Jing, Lu Hongyan

(College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China)

1 Introduction

LetG=(V(G),E(G)) be a connected simple graph with |V(G)| =nand |E(G)| =m. Ifm=n+c-1,thenGis called ac-cyclic graph. Specially, ifc=0,1 or 2, thenGis called a tree, a unicyclic graph or bicyclic graph, respectively. For verticesvi,vj∈V(G), the distancedG(vi,vj) is defined as the length of the shortest path betweenviandvjinG. LetD(G) =(dij)vi,vj∈V (G)be the distance matrix ofG,wheredij=dG(vi,vj). SinceD(G) is a symmetric real matrix, its eigenvalues are real. The maximum eigenvalue ofD(G) is called the distance spectral radius ofG, denoted byρ(G).

图1 图

In order to discuss our results, we first introduced some terminology and notation. Other undefined notation may refer to Ref[14]. Denote byPn,SnandCnthe path and the cycle onnvertices, respectively. LetGconsist of connected graphG1and pendant treesTi(1 ≤i≤k) with orderti, whereTi∩G1=vi. Vertexviis called the root of the treeTionG1. Ifti≥ 2, thenTiis called the nontrivial attaching tree toG1with rootvi(or rooted atvi). IfV(Ti)={vi}, thenTiis called the trivial attaching tree toG1. LetNG(v) be the neighbor set of vertexvinG. SetNG[v] =NG(v) ∪ {v}. The degree ofvinG, denoted bydG(v), is equal to |NG(v)|, i.e. the order ofNG(v). Letx= (xv1,xv2,… ,xvn) be the Perron eigenvector ofD(G) corresponding to the spectral radiusρ(G), in whichxvicorresponds tovi.

2 The transformations

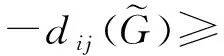
It is easy to see that:

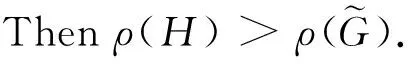
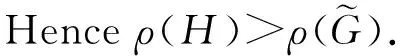
Lemma 3[6]Letwbe a vertex of the nontrivial connected graphGand for nonnegative integerspandq, letG(p,q) denote the graph obtained fromGby attaching pendant pathsP=wv1v2…vpandQ=wu1u2…uq. Ifp≥q≥ 1, thenρ(G(p+1,q-1)>ρ(G(p,q)).

Lemma 4[7]Supposeuvis a cut-edge of connected graphG, butuvis not a pendent edge. Letudenote the vertex obtained from identifyinguandvinGuv, andG′=Guv+uv, thenρ(G) >ρ(G′).

3 The bicyclic graph with minimal distance spectral radius in Bn

LetG*be the graph in Bnwith minimal distance spectral radius. Repeatedly by Lemma 4, we have the following two propositions.

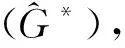
Ifqis odd, let

Note that for any vertexvt∈V(G*)V(Tu), all the path fromutovtwith lengthdG′(u,vt) passes only throughwor only throughvinG′. By Lemma 1, we haveρ(G′)<ρ(G*), it is a contradiction.

Ifqis even, let

or

by Lemma 2, we haveρ(G′)<ρ(G*), it is also a contradiction.

Henceq=3.

Similarly, we can provep=3.

Fig.2 The graph B(p1; q1, q2, q3, q4)图2 图B(p1; q1, q2, q3, q4)

Let

B(3, 1, 3) = {B(p1;q1,q2,q3,q4)|5 +p1+

Remark 1 In order to find the graphG*with minimal distance spectral radius in Bn, by Proposition 1-3, we only need to consider the graphs in B(3, 1, 3).

Proposition 4 Ifq1≥1,ρ(B(p1;q1,q2,q3,q4))>ρ(B(p1+q1;0,q2,q3,q4)).

Proof LetA1=B(p1;q1,q2,q3,q4),A2=B(p1+q1;0,q2,q3,q4), and

V1=NA1(u1),V2=NA1[u2],

V3=NA1[u3]∪NA1[u4],V4=NA1[v1].

Letxbe the Perron vector ofD(A2). By the Rayleigh quotient we have:

By the symmetry of components ofx, we can let:

From the eigenvalue equationD(A2)x=ρ(A2)x,we have:

ρ(A2)xu1=xv1+2(p1+q1)x1+xu2+2q2x2+

2xu3+3q3x3+2xu4+3q4x4,

ρ(A2)xu3=xv1+2(p1+q1)x1+2xu1+2xu2+

3q2x2+q3x3+xu4+2q4x4,

ρ(A2)xu4=xv1+2(p1+q1)x1+2xu1+2xu2+

3q2x2+xu3+2q3x3+q4x4,

ρ(A2)xv1=(p1+q1)x1+xu1+xu2+2q2x2+

xu3+2q3x3+xu4+2q4x4,

then

ρ(A2)(xu3+xu4+xv1-xu1)=xv1+3(p1+q1)x1+

5xu1+4xu2+6q2x2+2q3x3+xu4+2q4x4>0.

Note that

Henceρ(B(p1;q1,q2,q3,q4))>ρ(B(p1+q1;0,q2,q3,q4)).

Remark 2 Repeatedly by Proposition 4, we know thatρ(B(p1;q1,q2,q3,q4)>ρ(B(p1+q1+q2+q3+q4;0,0,0,0)).

Theorem 1 For a graphG∈Bn,ρ(G)≥ρ(B(n-5;0,0,0,0)),whereρ(B(n-5;0,0,0,0)) is the solution of the cubic equation inρ:

ρ3-(2n-7)ρ2-(7n-21)ρ-3n+7=0.

The equality holds if and only ifG≅B(n-5;0,0,0,0).

Proof By Remark 1 and 2, we haveρ(G)≥ρ(B(n-5;0,0,0,0)), and the equality holds if and only ifG≅B(n-5;0,0,0,0).

From the eigenvalue equationD(B(n-5;0,0,0,0))x=ρx, we have:

ρa=5a+b+2(n-5)c,

ρb=4a+(n-5)c,

ρc=8a+b+2(n-6)c.

Then we haveρ3-(2n-7)ρ2-(7n-21)ρ-3n+7=0.

[1] Consonni V, Todeschini R. New spectral indices for molecule description [J]. MATCH Commun Math Comput Chem, 2008, 60: 3-14.

[2] Gutman I, Medeleanu M. On the structure-dependence of the largest eigenvalue of the distance matrix of an alkane [J]. Indian J Chem A, 1998, 37: 569-573.

[3] Zhou B. On the largest eigenvalue of the distance matrix of a tree [J]. MATCH Commun Math Comput Chem, 2007, 58: 657-662.

[4] Zhou B, Trinajstic N. On the largest eigenvalue of the distance matrix of a connected graph [J]. Chem Phys Lett, 2007, 447: 384-387.

[7] Yu G, Wu Y, Zhang Y,et al. Some graft transformations and its application on a distance spectrum [J].Discrete Mathematics, 2011,311: 2117-2123.

[8] Bapat R B. Distance matrix and Laplacian of a tree with attached graphs [J]. Linear Algebra Appl, 2005,411:295-308.

[9] Bapat R B, Kirkland S J, Neumann M. On distance matrices and Laplacians [J]. Linear Algebra Appl,2005,401: 193-209.

[10] Indulal G. Sharp bounds on the distance spectral radius and the distance energy of graphs [J]. Linear Algebra Appl, 2009,430: 106-113.

[11] Zhang X L, Godsil C. Connectivity and minimal distance spectral radius [J]. Linear Multilinear Algebra,2001(1): 1-10.

[12] Balaban A T, Ciubotariu D, Medeleanu M. Topological indices and real number vertex invariants based on graph eigenvalues or eigenvectors [J]. J Chem Inf Comput Sci, 1991, 31: 517-523.

[13] Liu Z Z. On spectral radius of the distance matrix [J]. Appl Anal Discrete Math,2010(4): 269-277.

[14] Bollobás B. Modern graph theory [M]. Berlin: Springer, 1998.