基于广义成本的轨道交通最优路径模型研究

, , ,

(浙江理工大学机械与自动控制学院, 杭州 310018)

引 言

我国已有的高速铁路专线分布网络总长度已达到1.8万km,开通城市轨道交通运营线路的城市共有15座,运营长度总规模约1 746 km。预计到2020年,将会建成省会城市及大中城市间的快速客运通道,建设客运专线1.2万km以上[1]。随着轨道交通的发展,铁路接驳地铁的最优路径模型成为一个新的研究热点。传统的最优路径理论一般将路程最短、时间最短或费用最少作为最优路径,这种单目标的最优化往往带有片面性和局限性,难以符合现实状况。因此,建立基于多目标下的路径优化模型能为轨道交通最优路径模型的研究提供新思路。基于这一思路,Dial[2]提出了时间和费用双准则多目标最优路径模型,即时间约束下的最小费用路径模型。杨新苗等[3]设计了以换乘次数最少作为第一目标、出行距离最短为第二目标的双目标约束最优路径搜索和选择模型。柴登峰等[4]提出了广义最短路径问题,设计了一个递归调用Dijkstra算法,可以求取前N条最短路径的新算法。姚春龙等[5]提出了考虑多重目标的查询模型,通过权值设定来灵活调整目标的取舍问题。Jourquine等[6]给出了出行时间和路径选择的组合动态用户最优模型,利用出行费用和延迟成本求解模型。这些文献给出了多目标的最优路径模型和算法设计,但只是将目标作为约束条件,没有将多目标之间的关系进行转换。而且,这些文献也没有给出不同交通工具间换乘的计算模型。

本文提出将时间和成本两个目标统一成广义成本,建立基于广义成本下的轨道交通换乘最优路径模型,使之更加具有实际价值,应用Dijkstra算法求出的解也更为合理。

一、轨道交通换乘最优路径求解问题

(一)交通网络模型

轨道交通换乘路径求解问题可以描述为:已知乘客在铁路和地铁两种交通出行方式的情况下,找出从起点到终点的满足乘客需求的最优路径。其中换乘路径必须满足以下条件[7]:

(1) 出发点与目标点不属于同一条线路;

(2) 出发点与目标点必须是连通的;

(3) 出发点到目标点的路径不允许有回路。

将各站点进行分类,换乘站点:路线从一条线转入另一条线的必经站;关键站点:出度>3且不算是换乘站点的车站;一般站点:出度≤2的站。将换乘站点和关键站点作为交通网络的节点。

本文经过对轨道交通网络的分析,采用两级网络的层次模型。第一级网络模型:包括铁路以及地铁的所有车站、营运线名及其里程,也称物理模型。第二级网络模型:除去第一级网络中的中间站,仅取第一级网络中的关键站点、换乘站点以及拓扑结构。两级路网模型的对应关系如图1所示。可以看到,第二级网络模型的节点数明显减少,能够显著提高算法效率。

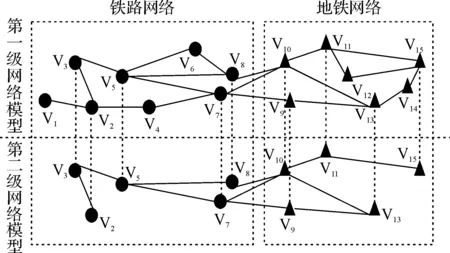
图1 两级路网模型的对应关系

二、广义成本下的二阶段换乘最优路径模型

(一)最优路径计算模型

1.时间成本模型

设G=为有向带权图,其中N={1,2,…,n}表示节点的集合,E={eij|i∈N,j∈N,i≠j}表示交通网络里的路段集合,M代表所有开车列车的车次集合,D代表节点之间的里程，T代表节点之间经历的时间,C代表节点之间的票价。两列列车在换乘站能够换乘的条件是:到车时间和发车时间间隔不小于最小的换乘时间,这里用T0表示。构建的时间成本模型:

Ttrain=Ttravel+Twait=

(1)

其中,

对城市轨道交通而言,只有发车频率和首末班时间,行车时间由路程长度与行车速度决定。设地铁速度为v,发车间隔频率为fk。在城市轨道交通的研究中,通常认为等车时间是发车频率的函数,计算公式如下[8]:

(2)

在两种不同的交通工具之间进行换乘时,必须添加一个惩罚因子[9],记作Tturn。因此,轨道交通换乘的时间成本模型函数为:

T(O,D)=β1(Ttravel×X铁路+T乘车×X地铁)+

β2(Twait×X铁路+Twait×X地铁)+β3×Tturn×Xturn=

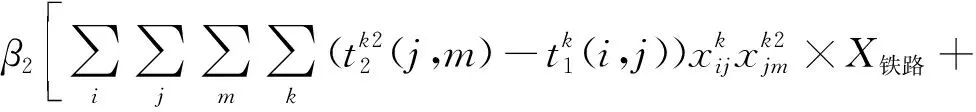
(3)

β1、β2、β3分别为各部分时间的重要性权值。

2.票价成本模型

城市轨道交通收费体系中票形式为里程票制[10]。里程票是指根据路程的长短确定票价,其票价函数形式为f(s)。因此,参照铁路的时间成本模型函数,地铁的成本函数为:

(4)

结合铁路及地铁的成本函数模型,得到轨道交通换乘的票价成本模型函数:

中医专业学生通过5年的本科学习，具备了较为扎实的中医学基本理论和基本技能，但普遍对中药化学成分、鉴别、炮制和制剂等知识缺乏了解，而中药是医生治疗疾病的重要武器，中药质量的好坏关系到药物疗效的发挥，最终会影响到患者的身体健康。所以随着中药现代化推进，中医专业研究生有必要加强中药化学成分、分析测试技术和现代制剂技术等知识的学习。

F(O,D)=

(5)

3.可靠性成本模型

可靠性成本是指交通工具到站时间的准点性、相邻交通工具间隔的均匀性及安全性。本文用出行时间中等待时间的偏差因子来衡量。理想状态下的等待时间为fk/2,因此,可靠性成本模型的函数为:

(6)

式(6)表明,在轨道交通等封闭环境较好的交通工具下,由于其准时性较高,可靠性成本可以不作考虑。

(二)票价成本对时间成本的转换模型

票价的单位为元,时间的单位是h(小时)。这两者之间可以通过时间行为价值的原理相互转化[11]。按照相关文献计算公式如下:

Bvot=Pwork×[Ywage/(50×40)-Bxiuxiam]+

(1-Pwork)×Bxiuxian

(7)

当Pwork为全国城市平均水平时,即Pwork=0.5时,得到票价成本对时间成本的转换函数为:

Bvot=Ywage/4000

(8)

(三)广义成本下的最优路径模型

广义成本是指由时间、票价、可靠性成本三部分构成的成本[8-9]。其形式为:

C(O,D)=CT(O,D)+CF(O,D)+CR(O,D)=

θ1ω1(T)T(O,D)+θ2ω2(F)F(O,D)+θ3ω3(R)R(O,D)

s.t.θ1+θ2+θ3=1,θ1,θ2,θ3>0

(9)

式(9)中,C(O,D)表示起点O和终点D间的广义成本;CT(O,D)表示起点O和终点D间的时间成本;CF(O,D)表示起点O和终点D间的票价成本。ω1(T)、ω2(F)、ω3(R)分别表示时间、票价和可靠性的量纲转化函数。T(O,D)、F(O,D)、R(O,D)分别表示时间函数、票价函数和可靠性函数。θ1、θ2、θ3分别表示时间、票价和可靠性的权重。

通过上述最优路径计算模型以及票价成本对时间成本的转换模型,最终得到基于广义成本下的轨道交通换乘最优路径的计算模型函数为:

minC(O,D)=

θ1ω1(T)×T(O,D)+θ2ω1(T)×(Ywage/4000)×

F(O,D)+θ3ω1(T)R(O,D)

(10)

三、Dijkstra算法

Dijkstra算法的基本思路是:假定V1→V2→V3→V4是V1→V4的最短路,如图2所示,则V1→V2→V3必定是V1→V3的最短路,V2→V3→V4必定是V2→V4的最短路。否则,设V1→V3的最短路为V1→V5→V3,就有V1→V5→V3→V4的路必小于V1→V2→V3→V4,这与假设矛盾。

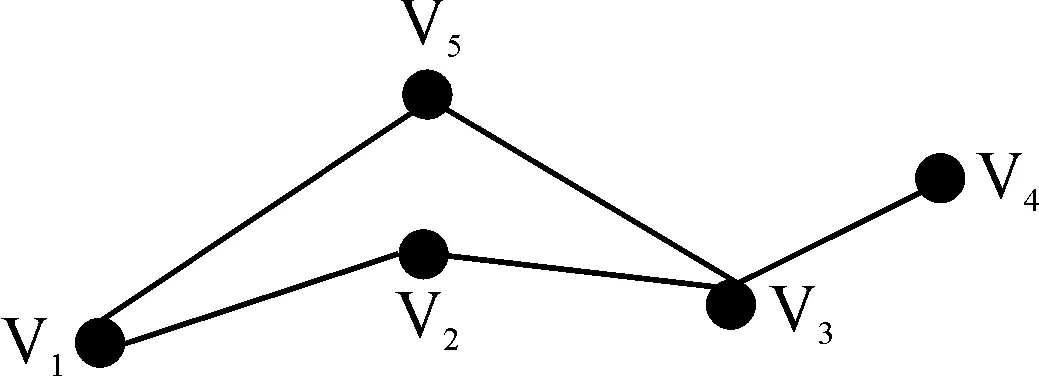
图2 Dijkstra算法思路

若用dij表示两相邻点i与j的距离,若i与j不相邻,则令dij=∞,显然dii=0。若用Lsi表示从s点到i点的最短距离,现求从s点到o点的最短路,用Dijkstra算法的步骤如下[12]:

(1) 从s点出发,因Lss=0,将此值标注在s旁的方框内,表示s点已标号;

(2) 从s点出发,找出与s相邻的点中距离最小的一个点,设为t。将Lst=Lss+ds的值标注在t旁的方框内,表明点t也已标号;

(3) 从已标号的点出发,找出与这些点相邻的所有未标号的点p。若有Lsp=min{Lss+dsp;Lst+dtp},则对p点标号,并将Lsp的值标注在p点旁的方框内;

(4) 重复第3步,一直到o点被标号为止。

Dijkstra算法主要用于静态路径的最优化模型,该算法也是目前公认的理论上较完善的算法,且简单易用。由于轨道交通本身具有封闭性好的特点,即受外界环境变化的影响很小。因此可以通过Dijkstra算法对基于广义成本下的轨道交通换乘最优路径模型进行求解。

四、模型仿真分析

以北京南站到上海同济大学为例,通过铁路运行时刻表和城市轨道交通运行表得到所有北京南站到上海的列车信息以及轨道交通的票价和发车频率。以高铁G157次列车为例,导入表1的数据,利用Matlab进行数据仿真。仿真参数:列车的等待时间为2 min;地铁的发车频率为每4 min一列;地铁的平均速度为75 km/h;按照相关文献调查及研究的成果将乘车时间相对重要性权值为1,等待时间相对重要性权值为2.1,换乘时间相对重要性权值为2.5[13];时间成本权值系数为0.26,票价成本权值系数为0.43,可靠性成本权值系数为0.31[14]。

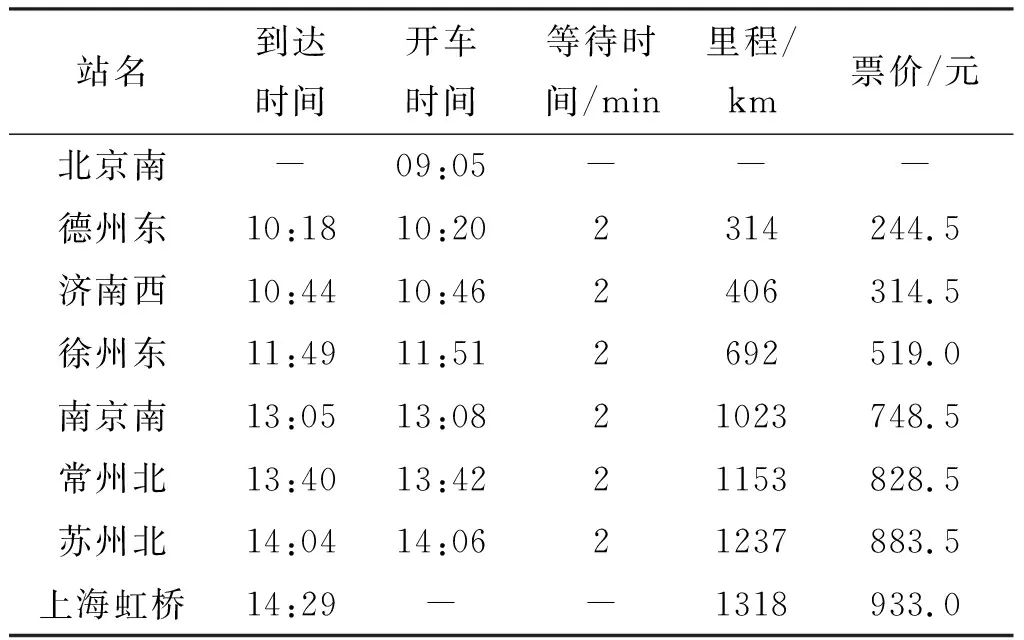
表1 G157次列车信息

通过仿真运行得到图3。从图3中可以看到,黑色箭头方向即为最优路径方向。依次经历的车站分别是北京南、沧州、济南、昆山南、上海南站、人民广场、上海体育馆、徐家汇、豫园、南京东路、四川北路、海伦路、同济大学。另外,通过仿真得到从北京南站到上海同济大学的最低广义成本为1 075元。综合仿真结果得出,仿真求得的最优路径较为合理,没有出现重叠交叉路径,且符合实际出行的规律。可见,本文提出的基于广义成本的轨道交通最优路径模型具有收敛性以及可行性。

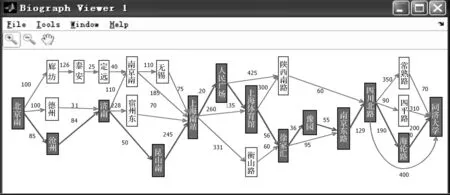
图3 可视化的最优路径

五、结 语

本文将行为时间价值理论应用于轨道交通换乘的多目标路径优化模型,提出了基于广义成本的轨道交通换乘最优路径模型,并采用两级分层的层次模型描述轨道交通网络,有效减少搜索节点的数量,提高了Dijkstra算法效率。最后通过Matlab进行实例仿真,验证了模型和算法的可行性和收敛性。本文的研究实现了多目标之间的关系转换以及两种交通工具之间换乘的模型计算,为多目标下的轨道交通换乘最优路径模型的研究提供了一些思路和方法。

文中仅考虑了铁路接驳地铁这两种运输环境较为封闭的交通工具之间的换乘,在将来的工作中,还需对更多交通工具组合方式下的换乘进行讨论,将经典的Dijkstra算法进行改进,以及针对外部环境不断变化的情况下,考虑采用更加适合和高效的算法进行优化求解。

参考文献：

[1] 陈文强, 吴群琪. 时间相关的运输网络最小费用路径模型及算法[J]. 铁道运输与经济, 2009, 31(5): 11-14.

[2] Dial R B. Transit pathfinder algorithm[J]. Highway Research Record, 1967, 205: 67-85.

[3] 杨新苗, 王 炜. 基于 GIS 的公交乘客出行路径选择模型[J]. 东南大学学报: 自然科学版, 2000, 30(6): 87-91.

[4] 柴登峰, 张登荣. 前 N 条最短路径问题的算法及应用[J]. 浙江大学学报: 工学版, 2002, 36(5): 531-534.

[5] 姚春龙, 王 昱. 基于权值设定策略的公交出行路径查询模型[J]. 计算机工程与应用, 2009, 45(11): 241-244.

[6] Jourquine B, Beuthe M. Transportation policy analysis with a geographic information system: the virtual network of freight transportation in Europe[J]. Transportation Research, 1996, 4 (6): 359-371.

[7] 余震江. 基于最短路径Dijkstra算法的铁路客运中转径路优化研究[D]. 重庆: 重庆大学, 2008.

[8] 柳晶晶. 基于多种换乘方式的公共交通路径选择模型研究[D]. 武汉: 华中科技大学, 2009.

[9] 白惠涛. 基于多种交通方式的城市快捷客运系统出行路径选择模型及优化方法研究[D]. 北京: 北京交通大学, 2007.

[10] 李春清. 城市公共交通换乘系统关键问题及评价研究[D]. 北京: 北京交通大学, 2008.

[11] 黄树森. 基于非集计的城市公共交通方式选择模型及灵敏度分析研究[D]. 北京: 北京交通大学, 2008.

[12] 张伯生. 运筹学[M]. 北京: 科学出版社, 2008: 175-176.

[13] 王 林. 车辆导航系统中最优路径算法的研究[D]. 葫芦岛: 辽宁工程技术大学, 2009.

[14] 张 帅. 基于ITS的智能乘客信息系统研究[D]. 郑州: 河北工业大学, 2004.