A study of quasi-absolute method in photon activation analysis∗

SUN Zai-Jing(孙在泾),D.Wells,C.Segebade,S.Chemerisov,and K.Quigley

1Chemical Sciences&Engineering Division,Argonne National Laboratory,9700 S.Cass Ave.,Argonne,IL 60439,United States

2Physics Department,South Dakota School of Mines&Technology, 501 E.Saint Joseph St.Rapid City,SD 57701,United States

3Idaho Accelerator Center,Idaho State University,921 S.8th Ave.Pocatello,ID 83209,United States

A study of quasi-absolute method in photon activation analysis∗

SUN Zai-Jing(孙在泾),1,†D.Wells,2C.Segebade,3S.Chemerisov,1and K.Quigley1

1Chemical Sciences&Engineering Division,Argonne National Laboratory,9700 S.Cass Ave.,Argonne,IL 60439,United States

2Physics Department,South Dakota School of Mines&Technology, 501 E.Saint Joseph St.Rapid City,SD 57701,United States

3Idaho Accelerator Center,Idaho State University,921 S.8th Ave.Pocatello,ID 83209,United States

Relative methods,which are performed with the assistance of reference materials,are widely used in photon activation analysis(PAA).On the contrary,absolute methods,which are conducted without any reference material,are rarely applied due to the difficulty in obtaining photon flux.To realize absolute measurement in PAA, we retrieve photon flux in the sample via Monte Carlo simulation and raise a novel procedure—quasi-absolute method.With simulated photon flux and cross section data from existing databases,it is possible to calculate the concentration of target elements in the sample straightforwardly.A controlled experiment indicates that results from the quasi-absolute method for certain elements are nearly comparable to relative methods in practice. This technique of absolute measurement has room for improvement in the future and can serve as a validation technique for experimental data on cross sections as well.

Photon activation analysis(PAA),Monte Carlo Simulation,LINAC

I.INTRODUCTION

Photon activation analysis(PAA),in most cases nowadays, is an accelerator-based radioanalytical technique.After the irradiation of the samples with high energy photons created by bremsstrahlung radiation of electrons,qualitative and quantitative information on the target elements can be obtained by detection of nuclear emissions following the irradiation with LINAC.The first article of PAA dated back to 1951 when Gaudin and Pannell of MIT tried to determine the amount of beryllium in low grade beryl ores by photodisintegration of Beryllium[1].They commented on this method as“rapid, simple,and nondestructive”.In 1954,Basile proposed to analyze some of the light elements using photonuclear reaction induced by bremsstrahlung radiation from a betatron[2]. His paper led to the wide use of the bremsstrahlung radiation as the high energy photon source of PAA.A chapter in Encyclopedia of Analytical Chemistry gave a brief but complete summary of PAA research[3].In recent years,PAA has expanded its applications in radiotherapy,meteorology, geochemistry,archeology,industrial material,environmental studies,etc.[4–10].

Figure 1 shows the basic principle of PAA.Photon activation usually occurs in the giant dipole resonance(GDR) region of the target nucleus.A high energy photon above the particle emission threshold enters the nucleus and interacts with nucleons.Then the excited nucleus equilibrates and turns into a statistical“compound nucleus”state.This“compound nucleus”will de-excite through residual strong interaction by emitting prompt gamma rays,neutrons,protons, and even alpha particles.Following the“compound”nucleusstage,the product nucleus generally is still unstable because it is usually a proton-rich(or neutron-rich)nucleus.It continues to de-excite to the final nucleus through weak interactions, such as electron capture and beta decay.Delayed gamma rays are emitted after those weak interactions.In most cases of PAA study,researchers concentrated on delayed gamma ray emission with a relatively long half-life.Those gamma rays can be detected by HpGe spectrometers and generated spectra with the assistance from computers.Hence,the procedure of PAA is quite straightforward:from the spectra of delayed gamma rays,one acquires their energy lines and intensity,which corresponds to certain product nuclides.From the information on the products nuclides,one can trace back to quantity and species of the target nuclides according to the corresponding nuclear reaction channels.

II.CALCULATIONS

According to Ref.[11–13],the net peak area(or counts)Pof the characteristic gamma line in the spectrum is

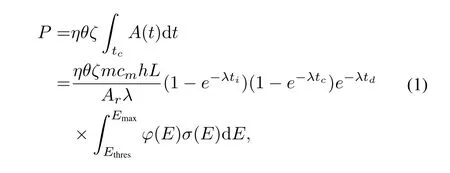
whereηis the detector efficiency,θis the branching ratio of the reaction channel,ζis the absolute intensity of the gamma line,Ais the activity of radioactive nuclide,mis the mass of the total sample,cmis the concentration of the nuclides of interest,his the natural abundance of the target nuclide,Lis the Avogadro constant,λis the decay constant of product nuclide,Aris the atomic mass of the target nuclide,ϕ(E)isthe energy differential photon flux,σ(E)is the cross section of the photonuclear reaction of interest,tiis the irradiation time,tcis the counting time,andtdis the decay time from the end of irradiation to the start of spectrum collection.

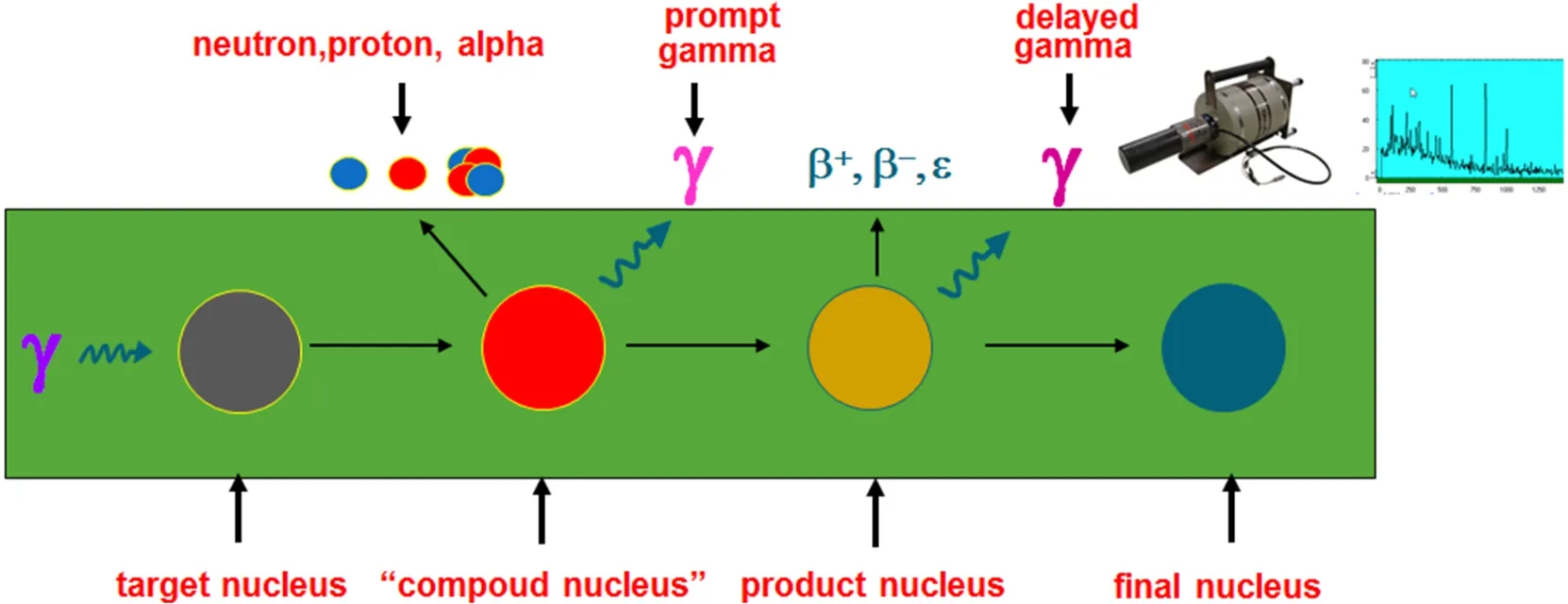
Fig.1.(Color online)Basic principle of PAA.

Equation(1)can be rearranged as

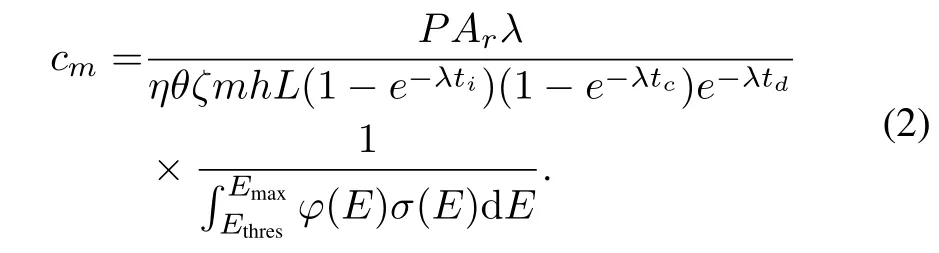
On the left side of Eq.(2)is the concentrationcmof a certain element in the sample,which is the ultimate value PAA seeks.On the right side mostly are the parameters we can measure(P,η,m,ti,tc,td),or parameters we can find the values in existing databases(θ,ζ,h,L,λ,Ar,σ(E)).The only parameter we normally cannot measure directly is the energy differential photon fluxϕ(E).

How to find the energy differential photon fluxϕ(E)?As mentioned before,we need assistance from computer simulations.From the simulated photon yield,it is feasible to derive photon flux and then calculate the concentration of the target nuclide directly based on the Eq.(2).

The output of the computer simulation is the photon yieldY(E).To obtain photon fluxϕ(E),one needs to multiply it with average beam current,Ibeam,of the LINAC as below.

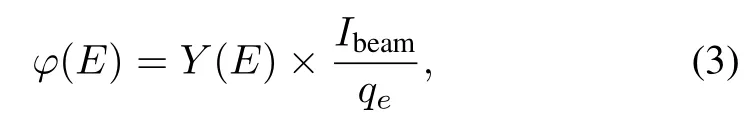
whereqeis the charge of an electron.Inserting Eq.(3)into Eq.(2),one gets

To simplify Eq.(4),we define the integral in the denominator as the reduced reaction rateIR,the Eq.(4)evolves into

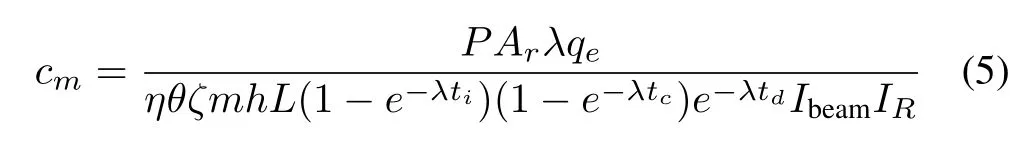
In Eq.(5),the uncertainty from atomic massAr,decay constantλ,electron chargeqe,detector efficiencyη,branching ratioθ,absolute intensityζ,natural abundanceh,Avogadro’s numberL,and time parameters(ti,tc,td)usually can be ignored.The primary source of uncertainty comes from uncertainty in the net peak areaP,mass of samplem, beam currentIbeam,and reduced reaction rateIR.Hence,the uncertainty propagation of Eq.(5)follows

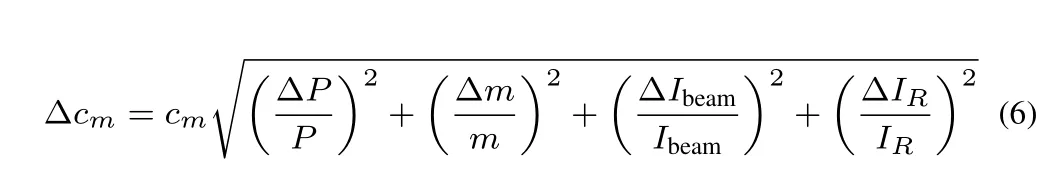
One should note that the uncertainty of the reduced reaction rate in Eq.(6)is the combination of the uncertainties of photon yield and cross sections.

III.EXPERIMENTAL SETUP,SIMULATIONS,CROSS SECITONS,AND PHOTON YIELD

A.Experimental setup

The experiment to realize quasi-absolute method was done by the 44MeVL-band pulsed LINAC at the Idaho Accelerator Center.In the experiment,the peak current is about 300mA,pulse width is 2.2µs,repetition rate is 120Hz,and the peak energy is about 30MeV.The side view of the experimental setup is shown in Fig.2.

Electrons are first produced by the hot cathode and then accelerated by a series of alternating RF electric fields in the acceleration cells.They form a focused electron beam from magnetic fields.The radius of the electron beam is around 3 millimeters.The energy distribution of the electrons(Fig.3) was measured with a Faraday cup,a magnetic spectrometer and beam-split to allow quasi-monochromatic electrons to pass after magnetic fields bend the track of electrons.

Aftertheelectronbeampassesthroughawatercoolingsystem and a path of air,it is absorbed by a 3mm-thick tantalum electron-photon converter(or radiator).Bremsstrahlung radiation is the primarily physical process in the radiator.After the radiator,the electron beam almost completely stops andthe newly generated photon beam strikes an aluminum hardener of about 3 inches thickness.The hardener absorbs the residual electrons and ensures that the beam out of the radiator is entirely made of high energy photons.

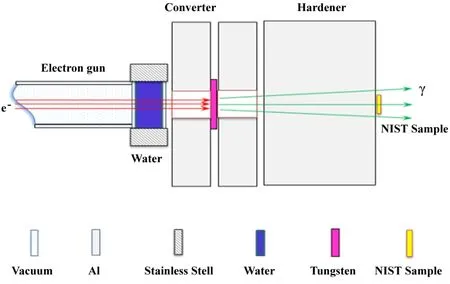
Fig.2.(Color online)Experimental setup of quasi-absolute method.

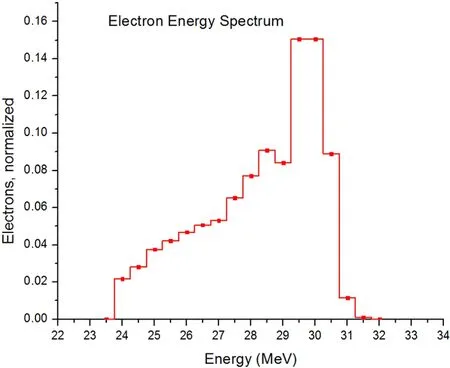
Fig.3.(Color online)Energy distribution of the electron beam of LINAC at 30MeV peak energy.

The urban particulate matter—standard reference material 1648a[14]—from NIST was chosen as the sample for verifying quasi-absolute method.It was selected because it is a well-known certified reference material and widely used in instrumental analytical methods.The sample was wrapped into a 1cm by 1cm square area with Aluminum foil and put behind the hardener along the beam axis.The thickness of the sample is about 1mm.

B.Photon beam simulations

Fig.4.(Color online)Geant4 simulation of“photon shower”in experiments for quasi-absolute method(view pointθ=45◦,ϕ=45◦).

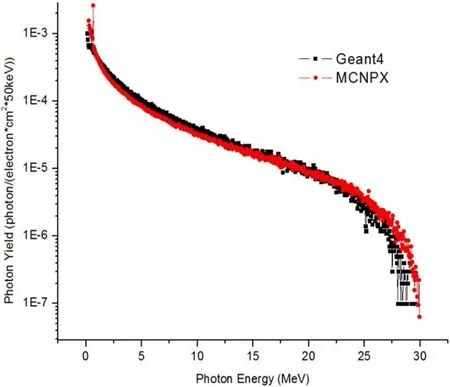
Fig.5.(Color online)Comparison of the simulated electron-photon yield with Geant4 and MCNPX(log scale).

Photon flux simulation was exactly based on the geometry and material of the experimental setup in Fig.2.The simulated photon flux is on the surface of the sample.Sample matrix effects(e.g.,in sample Compton scattering,γ induced further nuclear reactions,etc.)are not considered since the sample is small and thin.Geant4 is used as our primarily simulation software.MCNPX applied as an accessorial validation.The Geant4 toolkit we applied to the simulation is version 4.9.6[15].The class library of the high energy physics(CLHEP)used in this version is 2.1.3.1[16].The Geant4 toolkit is installed on a computer server running 64 bits GNU/Linux.The physics list of simulations includes all the electromagnetic processes,such as ionization,multiple scattering,positron annihilation,photoelectric effects,Compton scattering,pair production,and bremsstrahlung radiation. In the simulations,the total number of electrons we applied was 10 million.The statistical uncertainty from the simulation was small since we processed such a large number of electrons.

Figure 4 depicts the Geant4 simulation of a photon beam for the quasi-absolute method in PAA.In the figure,the yellow dot is the tracking point.The relationship of the track color and its corresponding particle is:photon–green, electron–red,positron–blue,neutron–yellow.The yellow square disk at the end of beam line is the sample.

Figure 5 shows the difference between simulated photon yields from Geant4 and those from MCNPX with the same geometry and materials shown in Fig.2.The two simulated results are consistent but with some slight variance.The percentage of differences is approximately 2%for the whole energy range(0～30MeV)and about 7.6%for the energy range of interest(10～30MeV)of PAA.The source of this discrepancy may originate from the different cross section libraries and the different algorithms used to implement calculation of electromagnetic processes in the two simulation codes.

C.Selection of cross sections

Ten photonuclear reactions were selected for realizing the quasi-absolute method(see Table 2).They were chosen based on the following criteria:(1)concentrations of their target nuclides are certified;(2)the target nuclides in this sample have a wide atomic number distribution:from light elements to heavy ones;and(3)their product nuclides have clear interference-free energy lines(pile-up can be ignored at the low counting rates in these experiments);(4)most of them are(γ,n)reactions.For the same isotope,the(γ,n)reaction channel has the largest cross sections in GDR region.

Original data of cross sections is in exchange format(EXFOR),which contains an extensive compilation of experimental nuclear reaction data[17–37].These records were retrieved and validated via a consortium of organizations,including the International Atomic Energy Agency(IAEA),the National Nuclear Data Center(NNDC),and the Center for Photonuclear Experiments(CDFE).Our criteria for choosing cross sections are:(1)find experimental reaction data and target isotopes as accurately as possible:(γ,n)data is preferred over(γ,total)and single target isotopes are preferred to targets with more than one isotope;(2)the cross section energy range should expand the energy range of interest(10～30MeV);(3)the data is as recent as available;(4) data from highly relevant sources in nuclear physics was preferred.

D.Photon yeild

With proper cross section data,we can apply quasiabsolute method by Eq.(5)if photon yield is available.Photon yield was obtained from photon beam simulations by the ratio between the number of photons in a certain energy bin and total incident electrons.The number of photons in different energy bins with different sizes was counted by the function“hist”in statistical software R[38].We tabulated the cross section data and photon yield and summed the products of them to obtain the reduced reaction rateIRand its corresponding uncertainty.Table 1 gives an example of this process.In Table 1,Eis the energy,σis cross section,Δσis uncertainty of cross section,“Energy Range”is the energy range centered onE,Np(E)is the number of photons in the energy range,Y(E)is photon yield in the energy range,Y(E)σ(E) is the reduced reaction rate in the energy range,ΔY(E)σ(E) is the uncertainty of reduced reaction rate in the energy range, andIRis reduced reaction rate.After having obtained the reduced reaction rateIRand its uncertainty ΔIR,we inserted them into Eq.(6)to calculate the estimated uncertainty for the quasi-absolute method.

IV.RESULTS AND DISCUSSION

Table 2 shows the experimental results from the quasiabsolute method.In Table 2,his natural abundance,Eis the energy line we chose for calculation,T1/2is the half-life of the product nuclides,Branch%is the absolute intensity of the energy lines,ηis the efficiency of the detector of that energy line,Iis the reaction rate which was calculated from the simulation and the cross section database,Pis the net peak area.cis the NIST certified value of concentration,cqis the concentration calculated from the quasi-absolute method,and“accuracy”is the discrepancy of the two values.The uncertainty of the NIST certified value is expanded uncertainty,with a coverage factor ofk=2(approximately 95%confidence)[14].The uncertainty from quasi-absolute method is calculated by the standard uncertainty propagation formulas.

From Table 2,one can see that the calculated value is close to the certified value for Ca,Mn,Co,Ni,and Zn;but apart for As,Rb,Sb,and Ce.The calculated concentrations are within a factor of two from the known concentrations.For some elements(e.g.As,Rb,Sb,and Ce),the results from the quasi-absolute method are considerably lower than the known concentration,close to a factor of two.This may stem from the fact that the cross section data we applied to those isotopes is an IAEA-tabulated total photonuclear cross section.For several elements(e.g.Ca,Mn,Co,Ni,and Zn),the calculated concentrations are reasonably close to the known concentrations(around 20%).For Zinc,two different reactions—(γ,n)and(γ,p)—reach very similar results.In addition,our results from the quasi-absolute method are systematically lower,which could mean that the simulated photon flux is higher than the real one.Many experiments have shown that simulated flux of standard Monte Carlo codes is higher than the real experimental flux by around 20%,according to different experimental setups and simulation programs[39–41].This difference may come from a combination of several factors,such as beam emittance,uncertainty of beam current,beam loading,beam wandering,cross sections, energy dissipation in experimental setup,etc.

Because of the limitations in measurement of experimental parameters,computer simulation of the Bremsstrahlung photon beam,and cross section data,the uncertainty of the quasi-absolute method may be still too high for practical usein precise radiochemistry and nuclear chemistry.In addition, thesystematicallyhigherphotonfluxofsimulationisasource of systematic error of the quasi-absolute method.

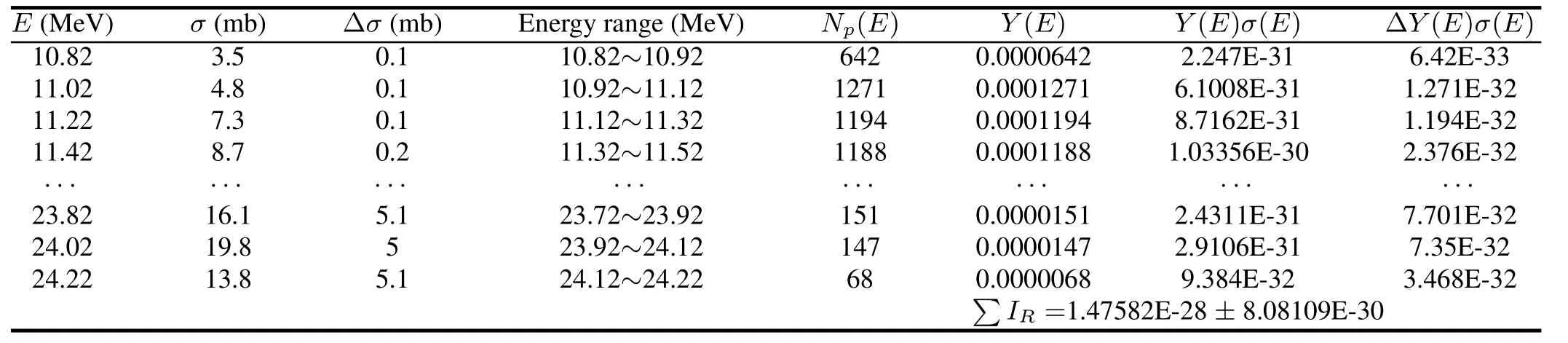
TABLE 1.Reduced reaction rate and its uncertainty for66Zn(γ,n)65Zn reaction

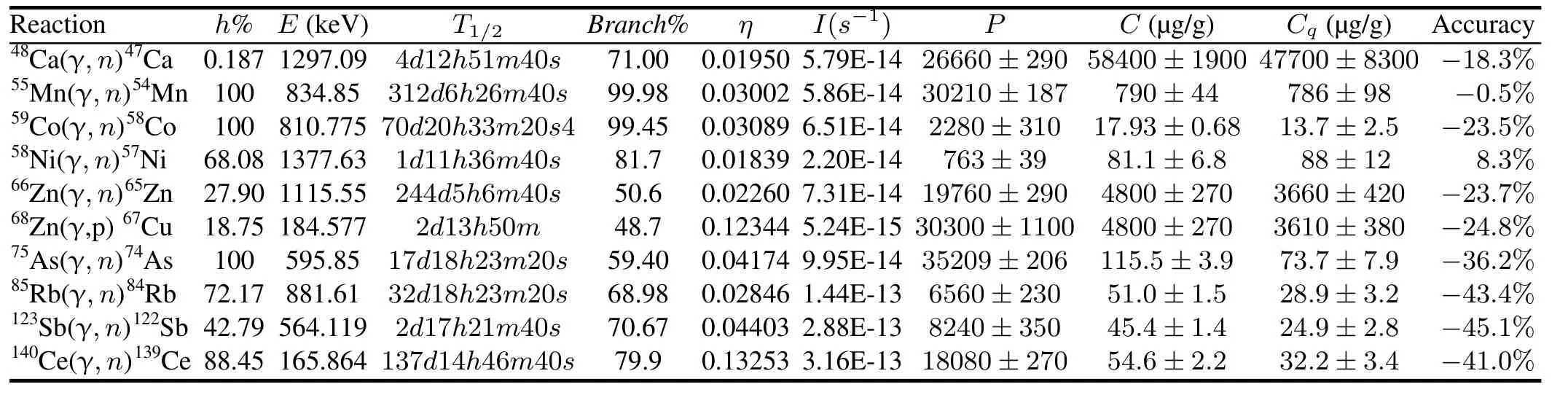
TABLE 2.Results from quasi-absolute method for NIST sample

V.CONCLUSION

We integrated the calculation of absolute measurement with the simulation of the bremsstrahlung photon yield and raised a question whether the quasi-absolute method could be developed and applied to practical radioanalytical chemistry. The experimental results show that the quasi-absolute method can be effective for some elements if the cross section data is accurate enough and simulated photon flux is close to a real situation.

Quasi-absolute method has its merit in practice and lots of room for further improvements:after systematic adjustment of photon flux and more accurate measurements on experimental parameters(especially photo-nuclear cross sections), it is possible to use the quasi-absolute method in actual radioanalytical practice for certain elements.On the other hand,if we havea prioriknowledge of elemental concentrations and a tagged photon beam,it is possible to invert the calculations to obtain valuable cross section information.Theoretically, thequasi-absolutemethodwillworkwellifthemeasurements and the corresponding simulation reach the required precision and accuracy.This should be a valuable direction in nuclear activation analysis.

[1]Gaudin A M and Pannell J H.Anal Chem,1951,23:1261–1265.

[2]Basile R,Hure J,Leveque P,et al.Comp Rend Acad Sci,1954,239:422–424.

[4]Ni J and Xu X G.Int J Environ An Ch,2000,78:117–134.

[5]Tsipenyuk Y M and Firsov V I.Appl Radiat Isotopes,2009,67:152–154.

[6]Goerner W.J Radioanal Nucl Ch,2008,276:251–255.

[7]Randa Z,Kucera J,Soukal L.J Radioanal Nucl Ch,2003,257: 275–283.

[8]Mamtimin M,Cole P L,Segebade C.AIP Conf Proc,2013,1525:400–406.

[9]Avino P,Capannesi G,Lopez F,et al.Scientific World J,2013: 458793.

[10]Avino P,Capannesi G,Manigrasso M,et al.Chem Cent J, 2013,7:173–182.

[11]Segebade C,Weise H P,Lutz G.Photon activation analysis. Berlin:Walter de Gruyter,1998,13–17.

林雪川的水业公司从2011年建立之后，经济效益一直不怎么理想。在和黎永兰确立了情侣关系之后，林雪川多次通过黎永兰向黎的家人借款。

[12]Sun Z J,Wells D P,Starovoitova V,et al.AIP Conf Proc,2013,1525:412–416.

[13]Sun Z J,Wells D P,Segebade C,et al.J Radioanal Nucl Ch, 2013,296:293–299.

[14]Wise S A.Certificate of analysis:standard reference material 1648a urban particulate matter,National Institute of Standards and Technology,2008.

[15]Geant4 Collaboration.Geant4 user’s guide for application developers.Geant4.9.6.0,November.European Organization for Nuclear Research,2012.

[16]Boudreau J W B and Cosmo C.CLHEP user guide,http: //proj--clhep.web.cern.ch/proj--clhep/ manual/.Accessed 10 July 2013.

[17]Veyssi`ere A,Beil H,Berg`ere R,et al.Nucl Phys A,1974,227: 513–540.

[18]AlvarezRA,BermanBL,LasherDR,etal.PhysRevC,1971,4:1673–1679.

[19]IAEA.Handbook on photonuclear data for applications cross–sections and spectra.I.A.E.A.TECDOC 1178.2000.

[20]Tompkins J R,Arnold C W,Karwowski H J,et al.Phys Rev C, 2011,84,044331.

[21]O′Keefe G J,Thompson M N,Assafiri Y I.Nucl Phys A,1987,469:239–252.

[22]Ahrens J,Borchert H,Czock K H,et al.Nucl Phys A,1975,251:479–492.

[23]Alvarez R A,Berman B L,Faul D D,et al.Phys Rev C,1979,20:128–138.

[24]Bazhanov E B,Komar A P,Kulikov A V.Pis’ma v Zh`Eksper Teoret Fiz,1964,46:1497–1499.

[25]Fultz S C,Bramblett R L,Caldwell J T,et al.Phys Rev,1962,128:2345–2351.

[26]Fultz S C,Alvarez R A,Berman B L,et al.Phys Rev C,1974,10:608–619.

[27]Owen D,Muirhead E,and Spicer B.Nucl Phys A,1970,140: 523–528.

[28]Goryachev B.Yadernaya Fizika,1970,11:252–256.

[29]GoryachevA.VoprosyTeoreticheskoyiYadernoyFiziki,1982, 8–121.

[30]Berman B L,Bramblett R L,Caldwell J T,et al.Phys Rev, 1969,177:1745–1754.

[31]Carlos P,Beil H,Berg`ere R,et al.Nucl Phys A,1976,258: 365–387.

[32]Varlamov V V,Peskov N N,Rudenko D S,et al.MSU-INP-2003-2/715.Engl transl of YK,2003,1–2,43–51.

[33]Leprˆetre A,Beil H,Berg`ere R,et al.Nucl Phys A,1971,175: 609–628.

[34]Katz L and Cameron A G W.Can J Phys,1951,29:518–544.

[35]Leprˆetre A,Beil H,Berg`ere R,et al.Nucl Phys A,1974,219: 39–60.

[36]Belyazv S.Izv Ross Akad Nauk,Ser Fiz,1991,55:953–956.

[37]Leprˆetre A,Beil H,Berg`ere R,et al.Nucl Phys A,1976,258: 350–364.

[38]Venables W N,Smith D M,the R Core Team.An introduction to R,Version 3.0.1.,2013.http://cran.r--project. org/doc/manuals/r-release/R-intro.html

[39]Faddegon B.Phys Med Biol,2008,53:1497–1510.

[40]Faddegon B.Med Phys,2008,35:4308–4317.

[41]Faddegon B.Med Phys,1990,17:773–785.

10.13538/j.1001-8042/nst.25.050201

(Received February 4,2014;accepted in revised form May 27,2014;published online September 15,2014)

∗Supported by the U.S.Department of Energy,Basic Energy Sciences, Office of Science(No.DE-AC02-06CH11357)

†Corresponding author,sunz@anl.gov