A fractionation model based on three lognormal particle size distributions

SHANG Jian-Bo(商建波),SHI Quan-Lin(师全林),WANG Qun-Shu(王群书),1,ZHONG Zhen-Yuan(钟振原),LEI Bei-Fang(雷北方),LIU Jie(刘杰),BAI Tao(白涛),DAI Yi-Hua(代义华),and LI Mou(李谋)

1Department of Engineering Physics,Tsinghua University,Beijing 100084,China

2Northwest Institute of Nuclear Technology,Xi’an 710024,China

A fractionation model based on three lognormal particle size distributions

SHANG Jian-Bo(商建波),1,2,∗SHI Quan-Lin(师全林),2WANG Qun-Shu(王群书),1,2ZHONG Zhen-Yuan(钟振原),2LEI Bei-Fang(雷北方),2LIU Jie(刘杰),2BAI Tao(白涛),2DAI Yi-Hua(代义华),2and LI Mou(李谋)2

1Department of Engineering Physics,Tsinghua University,Beijing 100084,China

2Northwest Institute of Nuclear Technology,Xi’an 710024,China

In this paper,a new model is proposed to calculate distribution of fi ssion products in particles of different sizes.The model sensitivity to the effective volume and mass of vaporized soil particles is examined.Compared with other fractionation models,the new method has a much better performance in calculatingr89,95,but the calculated cumulative activity fraction for particles in diameters over 100µm is in between the results using the F-T and G-X models.It is concluded that in a near surface nuclear explosion radioactivity is mainly distributed in soil particles which have not been vaporized,and according to the Henry’s law and ideal gas law,r89,95may vary in larger particles when effective volume of the fi reball is changed.

Fission products,Fractionation,Diffusion model

I.INTRODUCTION

A nuclear explosion generally produces fi ve effects:blast and shock,thermal radiation,electromagnetic radiation,initial nuclear radiation,and residual nuclear radiation(fallout) [1].Fallout plays an important role especially in ground nuclear explosion by creating a concentrated radioactive hazard causing potential damages to ecosystem in a relatively long period of time.Radioactive fallout must be evaluated to limit the ionization damages and provide guidance for formulating emergency plans in response to nuclear explosions.The total amount of radioisotopes and their distribution in particles of different sizes are determined by parameters of nuclear explosion,such as weapon yield,explosion height and soil type of ground zero.Therefore,computer simulation of the formation of radioactive particles in various explosions and quantitative analysis of the radioisotope distribution in different particles play an important role in fallout forecasting.It was found that the in fl uence coef fi cient of fractionation in radioactive fallout is over 2 according to researches conducted in Air Force Institute of Technology(AFIT),but fractionation models are still important for better understanding of explosion phenomena and evaluation of validity of samples[2].

Freiling-Tompkins fractionation model(also known as Modi fi ed Radial Power Law),Miller’s thermodynamic equilibrium model and Martin’s diffusion based G-X model are typical fractionation models[3–5].The G-X model was designed by Martin in 1980s,in which fallout particles are divided into two distinct types:glassy and crystalline.However,the total speci fi c activity of glassy and crystalline particles calculated with the G-X model varies much more greatly than the results of test observation.This can be attributed mainly to the different particle position in the fi reball.All the particles are drawn into fi reball at an early time,and different locations in the fi reball decide the speci fi c activitiesbecause of rapid changes in temperature and fi ssion product concentration in the fi reball.Also,some fi ne particles may come into being from condensation of the vaporized soil on separate atoms/molecules.After the soil particles begin to solidify,soil particles of smaller diameters are still drawn into cloud by after-winds,and are entirely un-melted.

Considering the particle formation process,the fallout particles can be divided into three types:1)particles from the device debris and vaporized soil,2)particles representing completely or partially melted soil,and 3)particles representing soil never melted.Based on the particle size and formation process,the three types of particles are referred to as fi ne particles,glassy particles and crystalline particles,respectively. With this classi fi cation,a new fractionation model was constructed to describe the distribution of radioactive nuclides in these particles.Taking into account that effective volume and the mass fraction of fi ne particles cannot be determined clearly,in fl uenceoftheresultfromeffectivevolumeandmass of fi ne particles was also examined.

II.METHOD AND PARAMETER SELECTION

A.Method

Calculation proceeds on one decay chain at a time when the fi reball temperature is about 3500K.After this point the isotopes are assumed to condense on surface of the particles according to Henry’s law and diffuse into the fallout particles. The isotopes decay with the time and the temperature falls. The process is repeated until the temperature is close to the solidi fi cation temperature for the glass.After this point,the fi ssion products in gaseous state will be distributed on surface of all types of particles.The amounts of the nuclides distributed in particles of different sizes and types are proportional to the total surface area of the particle group.

In the fi rst stage,only agglomeration between fi ne particles should be considered.Since all the fi ne particles are small enough to be considered nuclides volume-distributed,if weignore the diffusion process in the fi ne particles,there is no relation between the distributions of fi ssion products and the fi ne particle growth process.To simplify the model,we suppose that the fi ne particles of a constant mass at the fi rst stage grow up mainly by agglomeration.The diffusion equation for spheres with only radial diffusion is

whereciis the concentration of fi ssion producti,tis time of the diffusion process,ris the radial coordinate,andDiis the diffusion constant.According to the Henry’s law equation, the partial pressurePiof fi ssion productiis

wherekiis the Henry Constant andxiis concentration of fi ssion productiat the particle surface.

By dividing the fi rst stage into many small steps,at Step 1 we have the following mass balance by combing the diffusion equation,Henry’s law and ideal gas law:

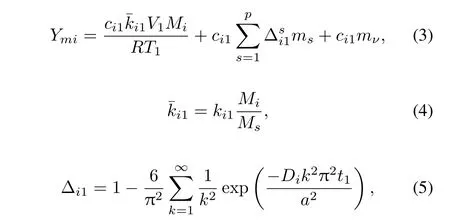
where subscriptidenotes the fi ssion product;Ymiis its massiin the fi rst time period;ci1is its surface layer concentration in the soil andki1is its Henry’s Law constant,at temperature of Step 1;Ris its gas constant;Miis its mole weight;msis the mass of soil in particle size classs;pthe number of particle size classes;mνthe mass of fi ne particles;andt1is the fi rst time period.On right side of Eq.(3),the fi rst term is the amount of fi ssion productiin gas phase,the second term is the amount of fi ssion productidiffused into melted soil particles by solving diffusion equation,and the third term is the amount of fi ssion productidiffused into fi ne particles formed mainly by vaporized soil.

The immediate precursor of isotopeiwhich diffused into particles in time interval Δt1may have decayed into isotopei.The in fl uence to diffusion of isotopeiin Step 2 by the mentioned process can be ignored if the time step is small enough. The mass balance equation after the second time period is

whereYi2isthemassof fi ssionproductiandci2isthesurface layer concentration ofiin the soil,in Step 2;λiis the decay constant ofi;andλi−1is the decay constant of precursor of isotopei.

This calculation goes iteratively until the temperature is close to the solidi fi cation temperature for the glass.In the second stage,the distribution of fi ssion productiin particles with different sizes and types is given by

whereYmsjis the mass of isotopeion the surface of thesthsize andjthtype particles,Ymνthe mass of gaseous istopeiafter stage 1,Surfjthe total surface fraction of thejthtype,mjthetotalmassofthejthtypeparticles,νjthemeanvolume of thejthtype particles andσjthe standard deviation.

B.Particle size distribution

Heft suggested that nuclear debris might be described by a linear combination of several lognormal distributions[6], which are distributions for each type of particles generated by the burst.The subsurface mass distribution is given by

whereϕiis the percentage of mass for theithtype of particles,σiis the standard deviation,andα0iis the natural logarithm of average diameter.

Based on Del fi c’s lognormal distribution and Baker’s airborne particle distribution,and with the knowledge that soil particles near ground zero of the Small Boy atom bomb are below 150µm in diameter,the values ofσiandα0iin this research are given in Table 1.

TABLE 1.The values ofσiandα0iin this research

C.Parameters selection

The main fi reball parameters in this research are the volume and temperature during the fi reball cooling to the solidi fi cation temperature of glass.The temperature is selectedfrom the Small Boy data.The fi reball size varied little after the fi reball breakaway,so the averaged fi reball volume is 106m3/kt in this research.

Normanet al.did many studies to determine Henry’s Law constants for those atomic species of interest in fallout research[7].Norman and others contributed a lot in determining diffusion constants of various soil types.The soil type of interest here is the CaO−Al2O3−SiO2soil,which is representative of common soils.The values of Henry’s Law constantsanddiffusioncoef fi cientsusedinthisresearcharelisted in Ref.[3].

Fission yield data and radioactive decay data are required for fi ssion product dynamic calculation.Independent fi ssion yield data together with radioactive decay data were selected from ENDF BVII.1[8].

III.RESULTS

A.Fractionation results

In a ground explosion,about 5000t of earth per kt of yield are released into the atmosphere and,of that quantity,180～200t are fused.The vaporized soil is 1.5～25t per kt.As the Small Boy is a nuclear explosion of low yield,3t vaporized soil particles and 1kt crystalline particles are assumed and 200t melted soil particles is determined[9].

To evaluate the model,the plots ofr89,95as a function of particle size is useful.The ratiori,jis de fi ned as

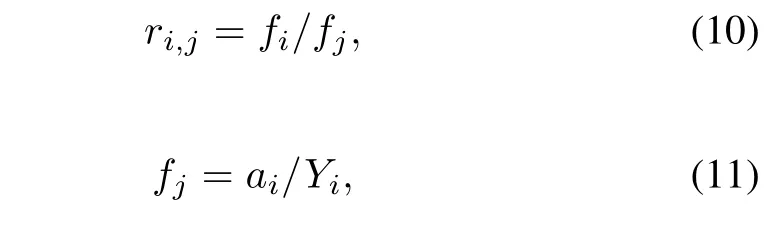
whereaiis the number of atoms of nuclideiin the sample corresponding to one fi ssion andYiis the yield of nuclideiper fi ssion.Log-log plots ofri,95versusr89,95values can be prepared and fi tted with linear least squares to determine the correlation slopes.

Ther89,95and the correlation slopes calculated by this model and G-X model are compared to the Small Boy data in Fig.1 and Table 2.The cumulate activity-size distribution calculated by this model with 3t vaporized soil particles and 1kt crystalline particles is compared in Fig.2 with the results using G-X and F-T models.

Figure 1 shows that our method better matches the Small Boy data above 100µm.The Small Boy data are mainly above 20µm,so the new method performs much better in calculatingr89,95.Fig.2 shows that our results of the cumulate activity fraction of particles over 100µm diameters,which mainly grounded in an area near ground zero after explosion, are between the results of the F-T and G-X models.But the logarithmic correlation slopes calculated with both models shows poor consistency with the Small Boy data,but the new model shows a poorer consistency in logarithmic correlation slopes of 131.Log-log plots ofr131,95versusr89,95of G-X model in Ref.[3]are cited,and the linear fi tting gives a slope of about 0.40 which varies much with the value given in Table 2 and is nearly equal with result of this model.As we cannot fi nd more information about how Martin fi tted the plots and logarithmic correlation slopes vary little when we changeeffective volume and fi ne particle mass fraction,we do not pay more attention to the logarithmic correlation slopes in later research.The current deviation of slopes of mass chain 91 and 140,where elements mainly affecting fractionation in the chain are mixed behavior elements whose distribution in fallout particles is appreciable gradient or some bulk loading, may suggest that diffusion constants used are overestimated.

Fig.1.(Color online)r89,95vs.particle size for different methods.

Fig.2.(Color online)Cumulate activity-size distribution for different models.

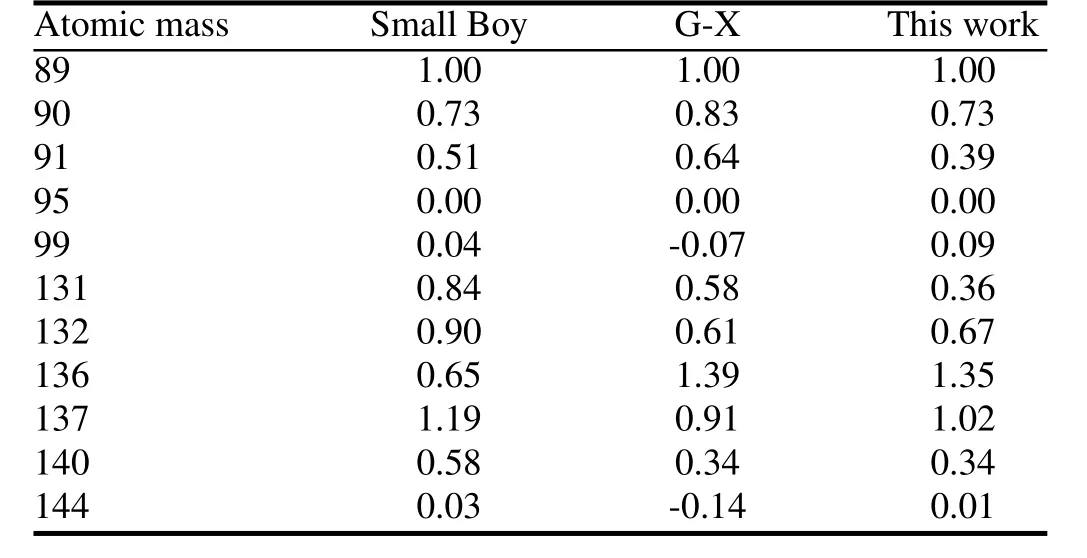
TABLE 2.The values ofσiandα0iin this research

B.Sensitivity analysis

1.Model sensitivity to effective volume

Since the fi reball experiences a rapid temperature and concentration fall,the effective volume in which the condensation process is involved is smaller than the physical volume of the fi reball.Ther89,95and activity-size distribution were shown in Figs.3 and 4,with 20%and 100%as the fraction of effective volume in the fi reball.

Fig.3.(Color online)Dependency of particle size onr89,95.

Fig.4.(Color online)Cumulate activity-size distribution.

Fig.5.(Color online)r89,95vs particle size for 0–15t mass of vaporized soil particles.

Fig.6.(Color online)Cumulate activity-size distribution for 0–15t mass of vaporized soil particles.

For particles of diameters over 1mm,as shown in Fig.3, ther89,95differ from each other for 20%and 100%fraction of effective volume,while the cumulate activity-size distributions remain unchanged.According to Henry’s law and ideal gas law,the fraction of fission products condensed in particles or still in gaseous state changes when effective volume varies.

2.Model sensitivity to mass of vaporized soil particles

In surface nuclear explosions,fine particles may form in the process of condensation on separate atoms/molecules. But mass fraction of the particles cannot be determined due to uncertainty of vaporized soil mass and the condensation process competition between the fine particles and melted soil particles.About 40t fine particles may form in an explosion of1.65ktweaponyield,butjust15tfineparticles wasused as a maximum value because of the low yield and about 3m explosion height.Ther89,95and activity-size distribution werecalculated for vaporized soil particle masses of 0t,3t and 15t(Figs.5 and 6).The results show that the mass of vaporized soil particles has no effect on ther89,95–size relation and the cumulate activity–size distribution hardly changes with the vaporized soil particle mass,as melted and un-melted soil particles involved are much more than the vaporized soil particles.

IV.CONCLUSION

Large quantity of soil entrained into the fireball by blast and updraft winds is not melted.We can assume that the unmelted soil particles do not play an important role in the condensation process of fission product on the particles,but they offer large surface areas for the gaseous fission product after condensation of the melted soil.Based on the Small Boy data near ground zero,Del fi c’s lognormal distribution and Baker’s airborne distribution,the particle size distribution is characterized and a new model is proposed to calculate the fi ssion product distribution on particles of different sizes.The new method has a much better performance in calculatingr89,95, and the cumulate activity fraction for particles in diameters of over 100µm is between the results calculated with the FT and G-X models.Model sensitivity analysis shows that ther89,95–size relation and the cumulate activity–size distribution are insensitive to both effective volume and mass of vaporized soil particles.It is concluded that in a nuclear explosion near surface,radioactivity is mainly distributed on the soil particles which have not been vaporized andr89,95may vary in larger particles when effective volume changes according to the Henry’s law and ideal gas law.

[1]Glasstone S and Dolan P J.The Effects of Nuclear Weapons (Third Edition).Alexandria V A:US Department of Defense and US Department of Energy,1977,1-4.

[2]Trabalka J R and Kocher D C.Bounding Analysis of Effects of Fractionation of Radionuclides in Fallout on Estimation of Doses to Atomic Veterans.Fort Belvoir(USA):DTRA-TR-07-5,2007.

[3]Martin C R.Ph.D.Thesis.Air Force Institute of Technology, 1983.

[4]Freiling E C.Science,1961,133:1991-1998.

[5]Freiling E C.Science,1963,139:1058-1059.

[6]Heft R E.Adv Chem Ser,1970,93:254-281.

[7]Norman J H.Henry’s Law Constants for Dissolution of Fission Products in a Silicate Fallout Particle Matrix,San Diego(USA), GA 7058,1966.

[8]McLaneV.ENDF-102Dataformatsandproceduresfortheevaluated nuclear data fi le ENDF-6.New York(USA),BNL-NCS-44945-01/04-Rev,2001.

[9]Izrael Y A.Radioactive fallout after nuclear explosions and accidents.Argyll,Scotland,UK:Amp fi eld House,2002,9-10.

10.13538/j.1001-8042/nst.25.050301

(Received December 25,2013;accepted in revised form March 3,2014;published online September 21,2014)

∗Corresponding author,shangjianbo@nint.ac.cn