一类超混沌系统的动力学研究及其仿真

张勇，张付臣，张光云，袁红

1.河南工业职业技术学院，河南南阳 473009

2.重庆大学数学与统计学院，重庆 401331

3.西南石油大学外国语学院，成都 610500

4.临沂大学理学院，山东临沂 276005

一类超混沌系统的动力学研究及其仿真

张勇1，张付臣2，张光云3，袁红4

1.河南工业职业技术学院，河南南阳 473009

2.重庆大学数学与统计学院，重庆 401331

3.西南石油大学外国语学院，成都 610500

4.临沂大学理学院，山东临沂 276005

1 引言

自从美国气象学家Lorenz发现第一个混沌系统-Lorenz系统以来[1]，混沌已经在许多领域中取得了巨大而深远的发展。尤其最近10多年来，混沌系统的控制和同步得到了广泛而深入的研究[2]。其中的许多结果都直接用到了混沌系统的解最终有界的假设，而这些系统的有界性大多数是通过计算机数值模拟得到的。直到2002年，文献[3]从数学上严格论证了Lorenz混沌系统吸引子的存在性以及最终有界性。对于著名的Lorenz系统，俄罗斯学者Leonov通过长期的研究，得到了Lorenz系统全局吸引集的一个圆柱形估计式和一个球形估计式。2005年，我国动力系统专家廖晓昕[4]等首次提出全局指数吸引集的概念，通过构造广义正定、径向无界Lyapunov函数族，结合其他数学方法，给出一个Lorenz系统全局吸引集和正向不变集的统一结果，并派生出其他一系列类似的公式，比Leonov的结果更精确。由于在全局指数吸引集Ω外一个混沌系统的平衡位置、周期解、概周期解、游荡回复解和其他任何混沌吸引子都不复存在，因此大大简化了对该混沌系统的分析工作。随后，其他一些混沌系统的全局指数吸引集相继被研究[5-15]。由于超混沌系统比一般的混沌系统的动力学行为更加复杂。因此，其动力学行为较一般混沌系统更加难以预测。据作者所知，对于超混沌系统的全局指数吸引集的问题研究的比较少，而且没有统一的方法来构造李雅普诺夫函数。因此，有必要对新超混沌系统的全局指数吸引集进行研究。下面将研究一类新超混沌系统的全局指数吸引集。

一个新超混沌系统为[16]：

其中a,b,c,d,e,f,g,h均为系统（1）的正参数，并且当a=35,b=4,c=25,d=5,e=35,f=100,g=1,h=1时，系统的李雅普诺夫指数分别是LE1=10.732 7,LE2=3.850 3,LE3=-3.439 9,LE4=-26.347 6，其最大的李雅普诺夫指数比较大且大于零，说明系统（1）的运动比较复杂，并且具有两个正的李雅普诺夫指数，因此系统（1）是超混沌的，其动力学行为较一般混沌系统（最大的李雅普诺夫指数为负）更加难以预测。此外该系统的李雅普诺夫指数维数是DL=3.422 9，由于该系统的李雅普诺夫指数维数是分数维，从而从另一方面验证了系统（1）是混沌系统。当a=35,b=4,c=25,d=5,e=35,f=100,g=1,h=1时，系统（1）轨线相图，见图1。

系统（1）的平衡点、李雅普诺夫指数、同步等问题在文献[16]中已经被研究过，但是超混沌系统（1）的全局指数吸引集问题至今没有被研究，下面将研究当正参数a,b,c,d,e,f,g,h满足a≥1,b＞1,c＞0,d＞0,e＞0,f＞0,g≥1,h≥1时，系统（1）的全局指数吸引集（在系统（1）中a=35,b=4,c=25,d=5,e=35,f=100,g=1,h=1)，有下面的定理。

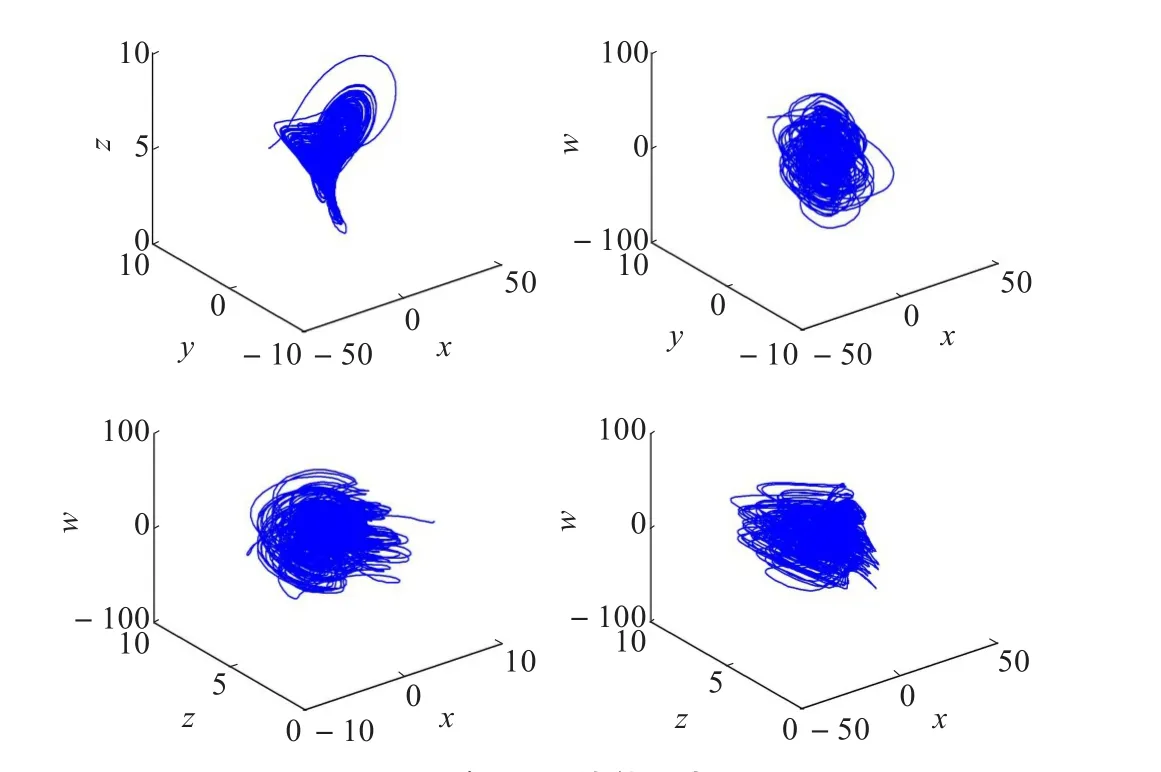
图1 系统（1）轨线的相图(a=35,b=4,c=25,d=5,e=35,f=100,g=1,h=1)

2 系统的全局指数吸引集

为系统（1）的全局指数吸引集。

证明作广义正定、径向无界的Lyapunov函数

沿着式（1）的正半轨线计算V(x,y,z)对时间t的导数，有

由定理1，系统（1）的正半轨线包含在下列所定义的四维椭球Ω之中。2所示。集合Ω1在xOy，xOw，yOw平面上的投影，如图3所示。取a=35,b=4,c=25,d=5,e=35,f=100,g=1,h=1[16]，取时间t=50 s，系统（1）的各个状态变量x(t),y(t),z(t),w(t)随时间演化的图形，如图4所示。

为方便起见，仅给出四维椭球Ω在xOyw平面上的投影

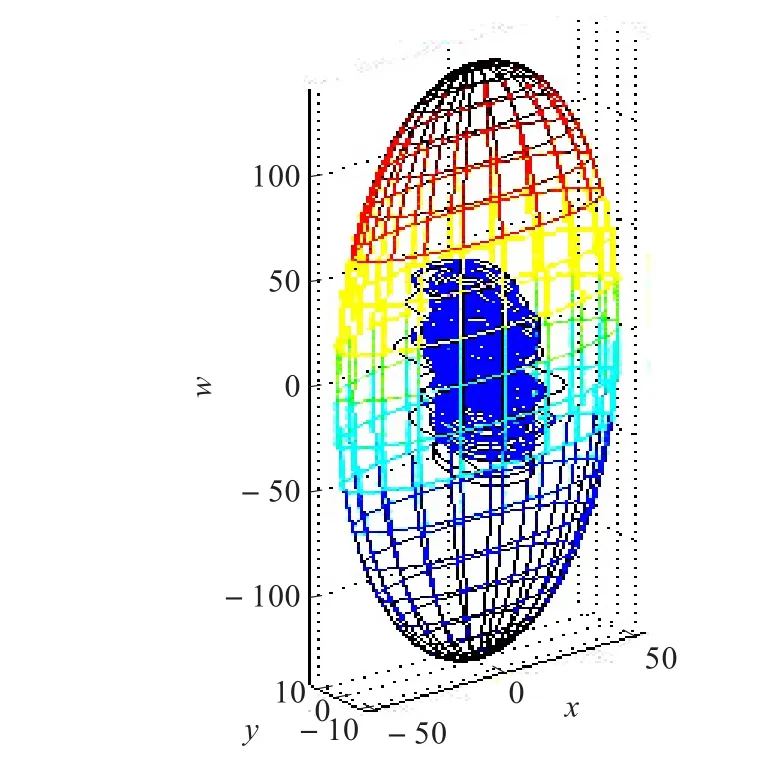
图2 系统（1）的正半轨线包含在三维椭球Ω1之内

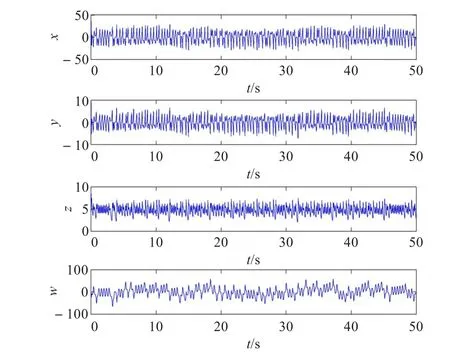
图4 系统（1）在上述参数下的各个变量随时间演化的曲线

与文献[16]中得到的该超混沌系统的界Ω2进行比较，可以看出本文中得到的该混沌的界范围相对较小，从而结果更加准确。

3 结论

本文通过构造合适的李雅普诺夫函数研究了一类新的不拓扑等价于Lorenz系统，Rossler系统，Chen系统，Lü系统的非线性自治超混沌系统（1），得到了该超混沌系统的全局指数吸引集Ω={x,y,z,w|7.142 9x2+100y2+ 250(z-11)2+w2≤20 166.7=(142)2},而且通过数学软件MATLAB给出了相应的数值模拟。仿真结果表明了该方案的有效性，同时也丰富了该混沌系统的混沌特性。由于全局指数吸引集的估计是通过广义Lyapuov函数获得的，正如Poincare地形线的作用一样Lyapuov函数控制系统轨线的走向。并且可以断定在全局指数吸引集Ω之外混沌系统（1）的平衡位置、周期解、概周期解、游荡回复解和其他任何混沌吸引子都不复存在。但是该系统的控制、同步、和复杂分岔行为等其他一些问题还有待于进一步研究。

[1]Lorenz E N.Deterministic non-periods flows[J].J Atmos Sci，1963，20：130-141.

[2]陈关荣，吕金虎.Lorenz系统族的动力学分析控制与同步[M].北京：科学出版社，2003.

[3]Stwart I.The Lorenz attractor exists[J].Nature，2002，406：948-949.

[4]Liao Xiaoxin.On the new results of global attractive set and positive invariant set of the Lorenz chaotic system and the applications to chaos control and synchronization[J].Science in China Ser FInformSci，2005，48：304-321.

[5]Liao Xiaoxin，Yu Pei.Study on the global property of the smooth Chua’s system[J].Internat J Bifur Chaos Appl Sci Engrg，2006，16：2815-2841.

[6]Li Damei，Lu Junan，Wu Xiaoqun.Estimating the ultimate bound and positively invariant set for the hyperchaotic Lorenz-Hakensystem[J].ChaosSolitonsFractals，2009，39：1290-1296.

[7]Wang Pei，Li Damei，Hu Qianli.Bounds of the hyper-chaoticLorenz-Stenflosystem[J].CommunNonlinearSci Numer Simul，2010，15（9）：2514-2520.

[8]Wang Pei，Li Damei，Wu Xiaoqun，et al.Ultimate bound estimation of a class of high dimensional quadratics autonomousdynamicalsystems[J].InternatJBifurChaos Appl Sci Engrg，2011，21（9）：2679-2694.

[9]Zhang Fuchen，Shu Yonglu，Yang Hongliang.Bounds for a new chaotic system and its application in chaos synchronization[J].Commun Nonlinear Sci Numer Simul，2011，16（3）：1501-1508.

[10]Zhang Fuchen，Mu Chunlai，Li Xiaowu.On the boundness of some solutions of the Lü system[J].Internat J Bifur Chaos Appl Sci Engrg，2012，22（1）：1250015-1-1250015-5.

[11]Zhang Fuchen，Shu Yonglu，Yang Hongliang，et al.Estimating the ultimate bound and positively invariant set for a synchronous motor and its application in chaos synchronization[J].Chaos Solitons Fractals，2011，（44）：137-144.

[12]舒永录，张付臣，杨洪亮.一个多维混沌系统及其性质研究[J].四川大学学报:自然科学版，2011，48（4）：857-864.

[13]杨洪亮，张付臣，舒永录，等.一个新三维类洛伦兹系统的最终有界集和正向不变集及其在同步中的应用[J].山东大学学报：理学版，2010，45（9）：83-89.

[14]袁红，张付臣.新混沌系统的全局指数吸引集及其数值模[J].计算机工程与应用，2012，48（11）：37-39.

[15]袁红，张付臣.多维混沌系统的全局指数吸引集及模拟[J].华中师范大学学报：自然科学版，2012，46（5）：518-521.

[16]张晓丹，崔丽娟.一类四维超混沌系统的界及同步的研究[J].物理学报，2011，60（11）：110511-1-110511-7.

ZHANG Yong1,ZHANG Fuchen2,ZHANG Guangyun3,YUAN Hong4

1.Henan Polytechnic Institute,Nanyang,Henan 473009,China
2.College of Mathematics and Statistics,Chongqing University,Chongqing 401331,China
3.School of Foreign Languages,Southwest Petroleum University,Chengdu 610500,China
4.School of Science of Linyi University,Linyi,Shandong 276005,China

Globally exponentially attractive set of a chaotic system plays an important role in chaos control and chaos synchronization.In this paper,the globally exponentially attractive set of a new hyper-chaotic system is studied via constructing a Lyapunov function and the function extreme value theory.It has been obtained that the globally exponentially attractive setΩfor this system.It can be concluded that the system cannot have equilibrium points,periodic solutions,quasiperiodic solutions,or other chaotic attractors outside the globally attractive setΩ.This simplifies the analysis of the properties of the hyper-chaotic system.Furthermore,it can be concluded that the rate of the trajectories of system going from the exterior of the setΩto the interior of the setΩis an exponential rate.The globally exponentially attractive setΩalso provides the theoretic foundation for the chaotic control and chaotic synchronization of the system.Numerical simulations are presented to show the effectiveness of the proposed scheme.Numerical simulation is consistent with the results of theoretical calculation.

hyper-chaotic system;globally exponentially attractive set;numerical simulations Lyapunov function

混沌系统的全局指数吸引集在混沌系统的控制与同步之中起着非常重要的作用。借助一个适当的Lyapunov函数和一元函数极值理论研究了一个新超混沌系统的全局指数吸引集，得到了该系统的全局指数吸引集表达式Ω。可以断定在全局指数吸引集Ω之外混沌系统的平衡位置、周期解、概周期解、游荡回复解和其他任何混沌吸引子都不复存在，这大大简化了对该系统的分析工作。确定轨线从吸引集外走向吸引集的速度是指数速率。同时得到的全局指数吸引集表达式Ω为该系统的控制和同步提供了理论依据。通过计算机进行了模拟，数值模拟与理论计算的结果相吻合。

超混沌系统；全局指数吸引集；数值仿真；李雅普诺夫函数

A

O241.84；O29；O242.1

10.3778/j.issn.1002-8331.1211-0340

ZHANG Yong,ZHANG Fuchen,ZHANG Guangyun,et al.Dynamical analysis of hyper-chaotic system and its simulation.Computer Engineering and Applications,2014,50（22）：79-82.

重庆市自然科学基金（No.2009BB3185）.

张勇（1981—），男，讲师，从事大学数学教学与研究；张付臣（1983—），主要研究领域为常微分方程稳定性与分岔；张光云（1983—），女，硕士研究生，研究方向：外国语言学与应用语言学。E-mail：zhangfuchen1983@163.com

2012-11-27

2013-01-05

1002-8331（2014）22-0079-04

CNKI网络优先出版：2013-02-07,http://www.cnki.net/kcms/detail/11.2127.TP.20130207.1420.020.html

◎网络、通信、安全◎