分布式隐私保护FHE-DBIRCH模型研究
2014-08-03刘英华
刘英华
(中国青年政治学院,北京 100089)
1 引言
自1995年提出隐私保护数据挖掘以来,隐私保护数据挖掘就成为了数据挖掘领域的研究热点和难点。隐私保护技术主要有数据扰动技术、匿名化技术和安全多方计算技术[1]。数据扰动技术隐藏了真实数据,挖掘者只能在被扰动的数据上挖掘知识(如添加了噪声、数据交换等);匿名化技术则是泛化和抑制操作微调了原始数据对象属性值,数据扰动技术、匿名化技术都改变了原始数据,即在被修改了的数据上完成挖掘任务。
聚类分析是数据挖掘研究的一个重要部分,是实现数据深层使用价值的一个重要步骤,也是其他挖掘任务的基础,聚类分析在数据挖掘领域得到了广泛的研究和应用[2]。可以将聚类分析作为单独的工具使用,分析、发现数据库中存在的知识和信息,并且对聚类分析的每一类总结其特点。针对聚类分析的某个类,还可以聚类二次分析出更深层次的知识和信息,并以此类推,进行聚类的n次分析,所以也可以认为聚类分析是其他数据挖掘模型中的一个预先处理过程[3]。
聚类分析是根据数据对象的相似度划分为若干个群组(簇),而隐私保护中的数据扰动技术、匿名化技术微调了原始数据对象属性值,这种操作将导致相似度计算值的误差,从而引起数据分布、密度特征的改变,进而影响群组的划分结果[4]。只有隐私保护中的安全多方计算技术,没有改变原始数据集,而是加密后传输,确保参与方信息的独立性和计算的正确性,同时又可以保护各参与方的信息不泄露给其他参与方或第三方。在基于安全多方计算技术隐私保护的数据集上完成聚类分析才能保证划分的群组与在原始数据上聚类分析划分的群组是完全一致的[5]。
本文提出的FHE-DBIRCH(Fully Homomorphism Encryption-Distribute Balanced Herative Reducing and Clustering using Hierarchies)模型是针对水平分布式数据存放模式,将各从数据集通过完全同态加密算法加密后发送到主数据集,并对主数据集的数据计算后解密,所有的计算对象均为加密后的数据。所以,半可信第三方数据挖掘者的聚类挖掘对象也是加密数据,无法重构原始数据,避免了原始数据的隐私泄露。理论证明了FHE-DBIRCH模型在聚类挖掘时对隐私的保护是可行的,并通过实验进行了验证。
2 问题描述
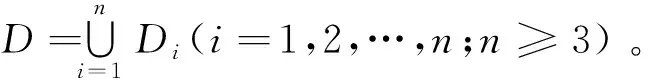
3 FHE-DBIRCH模型
为实现水平分布式数据集的隐私保护聚类挖掘,首先要实现各终端Ti到主数据集的隐私保护,首选的方法是加密技术[6~8]。
3.1 完全同态加密技术
完全同态加密FHE(Fully Homomorphism Encryption)技术是2009年由IBM研究员Gentry C首次提出的[9]。
定义1加密算法α,解密算法β,明文mi,运算符⊕和⊗。若存在公式α(β(m1)⊕β(m2)⊕…⊕β(mi))=α(β(m1+m2+…+mi)),即单个从数据集加密后进行的某种“加”计算后解密得到的结果,与单个从数据集“加”计算后加密后再解密得到的结果是相同的,则加密算法α和解密算法β基于运算符⊕满足同态加密。若存在公式α(β(m1)⊗β(m2)⊗…⊗β(mi))=α(β(m1×m2×…×mi)),则加密算法α和解密算法β基于运算符⊗满足同态加密。若两个公式均存在,则加密算法α和解密算法β基于运算符⊕和⊗满足完全同态加密。
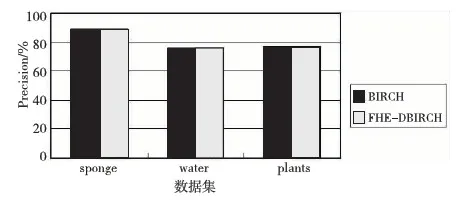
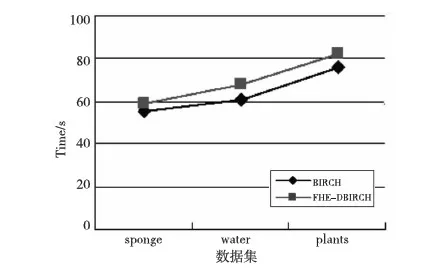
算法1加密数据为m,密钥是大数p(一个大数),大数k(随机生成,且k符合条件m< 加密算法:E(m)=qp+kr+m; 解密算法:D(E(m))=(E(m) modp)modk。 则算法1是一个符合完全同态加密的算法。 证明假设E(mi)=qip+kri+mi,则有: E(m1)+E(m2)+…+E(mi)= (q1+q2+…+qi)p+(r1+r2+…+ri)k+(m1+m2+…+mi) 因为(r1+r2+…+ri)k+(m1+m2+…+mi)< D(E(m1)+E(m2)+…+E(mi))=((E(m1)+E(m2)+…+E(mi)) modp) modk=(k(r1+r2+…+ri)+(m1+m2+…+mi)) modk=m1+m2+…+mi 则有E(m1)×E(m2)×…×E(mi)= (γ)p+(δ)k+(m1×m2×…×mi), 其中(γ)p表示p的倍数,(δ)k表示k的倍数, 因为(δ)k+(m1×m2×…×mi) < D(E(m1) ×E(m2)× …×E(mi))=((E(m1)×E(m2)×…×E(mi))modp) modk=((δ)k+(m1×m2×…×mi)) modk=m1×m2×…×mi得证。 □ 加密算法E(m)的时间复杂度为O(1),解密算法D(E(m))的时间复杂度为O(1)。 分布式BIRCH(DBIRCH) 模型针对主数据集、从数据集分布式存储结构,将各从数据集Di(i=1,2,…,n;n≥3)计算出CFi树后发送到主数据集,主数据集联合从数据集发来的CFi树构建联合数据集CF树(即主CF树)。然后,采用PAM算法对主CF树的叶节点进行聚类,删除离群点(即稀疏的簇),合并稠密簇。 算法2分布式BIRCH算法 输入:各站点数据集Di,每个Di对象个数mi(i=1,…,n;n≥3),B值(任何的非叶节点可以拥有的孩子数目),L值(叶子节点最多拥有的元组数目),聚簇个数k。 输出:k个聚簇。 分布式BIRCH算法——主数据集: (1)fori=1 ton (2)接收各站点发来的CFi树 (3)end for (4)构建主CF树 ①设CF1的根节点是主CF树的根节点,非叶子节点根据root(CF1)逐级确定最近的子节点; ②叶子节点则计算最接近的元组Li可否吸收; i.是,更新CF值; ii.否,判定是否增加新元组; a)是,增加新元组; b)否,分裂距离最远的元组,并将其作为种子分配给距离最近的元组; ③更新每一个非叶子节点的CF值,若分裂此节点node,则在parent(node)插入新元组直至分裂到根节点; ④合并:若在Nj节点(非叶子节点)不再分裂,则将离Nj最近的两个节点的元组合并。 ⑤输出主CF树; (5)在CF树中任选k个叶子节点; (6)repeat (7)分配剩余叶子到最近的代表对象所代表的簇; (8)递归修改CF树中非叶子节点的CF值; (9)随机选择对象O并计算O交换Oj的代价; (10)若代价<0,则Oj=O; (11)until 不再发生变化; 分布式BIRCH算法——从数据集: (1)fori=1 ton (2)从根节点开始逐级确定非叶子节点最近的子节点; (3)若是叶子节点,则计算最接近的元组Li可否吸收; ①是,更新CF值; ②否,再次判定可否增加一个新元组; i.是,更新CF值; ii.否,分裂距离最远的元组,并将其作为种子分配给距离最近的元组; (4)更新除叶子节点外的其他节点的CF值,若分裂此节点node,则为parent(node)插入新元组,直至分裂到根节点; (5)合并:若在Nj节点(非叶子节点)不再分裂,则将离Nj最近的两个节点的元组合并; (6)发送CFi树到主站点; (7)end for FHE-DBIRCH算法的基本思想是在从数据集计算CFi值,然后加密传输到主数据集;主数据集对密文进行某种计算后,解密后再构建联合数据集CF树(即主CF树)。然后,采用PAM算法对主CF树的叶节点进行聚类,删除离群点(即稀疏的簇),合并稠密簇。最后,将主站点计算的k个簇的集合广播给各从站点Si。 模型中传输的数据均为加密数据,保证了原始数据的隐私性,但因为加密、解密操作增加了额外开销,必然导致FHE-DBIRCH模型的运行时间高于DBIRCH模型。 算法3FHE-DBIRCH算法 输入:各站点数据集Di,每个Di对象个数mi(i=1,…,n;n≥3),B值(任何的非叶节点可以拥有的孩子数目),L值(叶子节点最多拥有的元组数目),聚簇个数k。 输出:k个聚簇。 FHE-DBIRCH算法——主数据集: (1)fori=1 ton (2)接收各站点发来的加密CFi树,根据解密算法得到CFi树; (3)end for (4)构建主CF树; ①设CF1的根节点是主CF树的根节点,非叶子节点根据root(CF1)逐级确定最近的子节点; ②叶子节点则计算最接近的元组Li可否吸收; i.是,更新CF值; ii.否,判定是否增加新元组; a)是,增加新元组; b)否,分裂距离最远的元组,并将其作为种子分配给距离最近的元组; ③更新除叶子节点外的其他节点的CF值,若分裂此节点node,则为parent(node)插入新元组直至分裂到根节点; ④合并:若在Nj节点(非叶子节点)处不再分裂,则将离Nj最近的两个节点的元组合并; ⑤输出主CF树; (5)在CF树中任选k个叶子节点; (6)repeat (7)分配剩余叶子到最近的代表对象所代表的簇; (8)递归修改CF树中非叶子节点的CF值; (9)随机选择对象O,计算O交换Oj的代价; (10)若代价<0,则Oj=O; (11)until 不再发生变化; FHE-DBIRCH算法——从数据集: (1)fori=1 ton (2)从根节点开始逐级确定非叶子节点最近的子节点; (3)叶子节点则计算最接近的元组Li可否吸收; ①是,更新CF值; ②否,再次判定可否增加一个新元组; a)是,更新CF值; b)否,分裂距离最远的元组,并将其作为种子分配给距离最近的元组; (4)更新除叶子节点外的其他节点的CF值,若分裂此节点node,则为parent(node)插入新元组直至分裂到根节点; (5)合并:若在Nj节点(非叶子节点)处不再分裂,则将离Nj最近的两个节点的元组合并; (7)end for 实验平台是具有以下参数的PC机:赛扬2.6 GHz CPU,4 GB内存,1 TB硬盘,Windows XP操作系统。本实验随机挑选了UCI中的三个数据集,在Weka平台下封装了FHE-DBIRCH算法,对三个数据集分别实现BIRCH算法和FHE-DBIRCH算法的对比实验。 评价聚类挖掘结果的重要指标之一是聚类精度,聚类精度是用有明确的分类结构的数据作为输入样本,对比聚类结果和数据原来的分类结构,以评价聚类算法的优劣[10]。 因为采用FHE-DBIRCH算法的从数据集传输时均为加密后的数据,其他数据集都不能获取其他从数据集的明文数据,所以FHE-DBIRCH算法避免了从数据集的隐私泄露。本文的FHE-DBIRCH算法符合完全同态加密,因此FHE-DBIRCH算法与不加隐私保护的聚类算法得到的聚类结果完全一致,即聚类精度一致。实验结果如图1所示。 Figure 1 Comparison of clustering accuracy图1 聚类精度比较 FHE-DBIRCH算法需要加密解密过程,因此时间成本增加,相对不加隐私保护的BIRCH算法成本增加小于15%,如图2所示。 Figure 2 Comparison of execution time图2 执行时间比较 本文针对水平分布式环境中聚类数据挖掘算法中存在的隐私泄露问题,提出了一种完全同态加密FHE-DBIRCH模型。该模型将水平分布式数据分为主、从两个数据集,采用完全同态加密算法对从数据集的数据进行加密,加密后的从数据集传送到主数据集,主数据集对加密后的从数据集计算后得到结果再解密。 这样的结果与各从数据集直接计算得到的结果是一致的。通过理论证明和实验数据的分析均确认该模型可以保护水平分布式数据的隐私,在加密的同时实现聚类挖掘。 [1] Zhou Shui-geng, Li Feng, Tao Yu-fei, et al. Privacy preservation in database applications:A survey[J]. Chinese Journal of Computers, 2009, 32(5):847-860.(in Chinese) [2] Han Jia-wei. Data mining concepts and techniques[M]. Beijing:China Machine Press, 2001.(in Chinese) [3] Chong Zhi-hong, Ni Wei-wei, Liu Teng-teng, et al. A privacy-preserving data publishing algorithm for clustering application[J]. Journal of Computer Research and Development, 2010,47(12):2083-2089.(in Chinese) [4] Gentry C. Fully homomorphic encryption using ideal lattices[C]∥Proc of the 41st Annual ACM Symposium on Theory of Computing (STOC’09), 2009:169-178. [5] Kamakshi P, Babu A V. Preserving privacy and sharing the data in distributed environment using cryptographic technique on perturbed data[J]. Journal of Computing, 2010, 2(4):115-119. [6] Vaidya J, Clifton C W, Zhu Y M. Privacy preserving data mining[M]. Purdue:Springer, 2006. [7] Vaidya J, Clifton C. Privacy-preserving K-means clustering over vertically partitioned data[C]∥Proc of the SIGKDD’ 03, 2003:24-27. [8] Kumar K A, Rangan C P. Privacy preserving DBSCAN algorithm for clustering [J].Advanced Data Mining and Applications, 2007, 4632:57-68. [9] Gentry C. Fully homomorphic encryption using ideal lattices[C]∥Proc of Symposium on the Theory of Computing (STOC), 2009:169-178. [10] Halkidi M, Vazirgiannis M, Batistakis Y. Quality scheme assessment in the clustering process[C]∥Proc of PKDD Conference, 2000:265-276. 附中文参考文献: [1] 周水庚,李丰,陶宇飞,等. 面向数据库应用的隐私保护研究综述[J]. 计算机学报,2009, 32(5):847-860. [2] 韩家炜.数据挖掘概念与技术[M].北京:机械工业出版社,2001. [3] 崇志宏,倪巍伟,刘腾腾,等. 一种面向聚类的隐私保护数据发布方法[J]. 计算机研究与发展,2010,47(12):2083-2089.3.2 分布式BIRCH模型
3.3 隐私保护FHE-DBIRCH模型
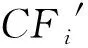
4 实验结果和分析
5 结束语
