基于最小二乘支持向量机的电站锅炉吸热面积灰监测研究

刘正峰 王景成 史元浩

(上海交通大学自动化系系统控制与信息处理教育部重点实验室,上海 200240)

电站锅炉运行中，受热面的积灰结渣是不可避免的。灰污的热阻很大，导致锅炉受热面的吸热量减少，降低锅炉的热效率；严重的积灰会使锅炉运行变得不稳定，甚至造成安全事故。而我国电站燃煤往往呈现煤种多变、煤质差的状况，造成锅炉受热面更容易积灰结渣。对受热面进行吹灰是有效的解决办法，吹灰介质一般是空气或者蒸汽，目前我国燃煤电站锅炉大多是进行定时定量吹扫操作。这样一方面会由于高温高压蒸汽的消耗而造成效率降低，另一方面也会因为不合理的吹扫而影响受热面的寿命。因此，对受热面的吹灰操作进行优化是亟待解决的问题之一，而其前提就是对受热面的积灰状况进行准确的监测。

近年来，学者对燃煤电站锅炉受热面积灰监测做了许多工作。目前主要的方法有：理论机理模型[1]、热平衡法[2]和神经网络法[3]。朱予东等根据热平衡原理，建立了热力计算模型[2,4]。陆继东等利用神经网络方法建立了受热面清洁吸热量预测模型，计算出灰污特征参数，进而对积灰状况进行监测[5]。徐啸虎等基于能量守恒和换热过程一般原理，建立了灰污染损失的计算模型[1]，包括排烟温度偏差和传热量偏差两个子模型。建模和偏差分析过程均不涉及任何线性化的数学处理，模型可用于定量分析锅炉系统因灰污染引起的传热性能和效率变化，并确定最佳经济性吹灰时间。

最小二乘支持向量机LSSVM是以二次损失函数为经验风险的支持向量机，它以等式约束代替不等式约束，将模型的训练转化为线性方程组的求解，简化了计算，缩短了训练时间，且训练结果更具确定性，适合对清洁吸热量的预测进行在线应用[6]。

笔者基于最小二乘支持向量机和粒子群算法，以某300MW燃煤机组为研究对象，对电站锅炉热工数据处理分析后，建立锅炉低温过热器受热面清洁吸热量模型。基于所建立的模型，选取机组正常运行工况下的数据，预测清洁吸热量，并计算实际吸热量，得到清洁系数，绘制出受热面的积灰曲线，从而实现对锅炉受热面积灰的在线监测。

1 燃煤电站锅炉对流受热面积灰监测方法①

1.1 积灰特征参数选取

传统的积灰特征参数一般选择灰污系数，这既涉及到工质侧参数，也需要烟气侧的参数，这在实际应用中有比较大的限制[7]，因此，笔者选取更方便的积灰特征参数。

受热面积灰后，直接受到影响的是工质吸热量的减少，所以将对流受热面吸热量选为对比参数值，引入表征受热面积灰程度的特征参数——清洁系数K：

(1)

式中Qqj——相同运行工况条件下，工质在受热面清洁状态下的吸热量，简称清洁吸热量；

Qsj——对流受热面工质实际状态下的吸热量，简称实际吸热量。

显然，清洁系数K介于0～1之间，当受热面清洁时，K趋近于1；随着受热面污染程度加重，K逐渐减小，趋近于0。

1.2 吸热量计算

锅炉运行时对流受热面工质的实际吸热量Qsj可以用下面的公式求得：

Qsj=Dgz(h2-h1)

(2)

式中Dgz——工质流量，kg/s；

h1——受热面入口工质焓，kJ/kg；

h2——受热面出口工质焓，kJ/kg。

出入口的工质焓值可以通过工质压力与温度计算得到。工质压力及进出口工质温度等工质侧参数在现有大型电站锅炉的数据采集系统(DAS)中一般都可准确获得。涉及到的饱和水蒸气和过热蒸汽的焓值计算，可以通过IAPWS-IF97的水和水蒸气性质表查得[8]，也可以根据IAPWS-IF97的水和水蒸气性质表的数据自行拟合。笔者通过基于IAPWS-IF97的水和水蒸气性质所编写的程序计算得到工质焓值[9]。因此，实际吸热量Qsj可由式(2)计算得到。

而在相应工况下，由于受热面处于非清洁状态，受热面的清洁吸热量Qqj不能通过式(2)直接得到。受热面的清洁吸热量与受热面污染情况无关，只由相应运行工况决定。因此，受热面清洁吸热量Qqj与实际运行工况参数构成一个随时间连续变化的非线性动态系统[7]。因此，可以选取合适的算法建立模型来预测Qqj。

相对于高温过热器，在低温过热器的灰污检测中，可以增加入口烟温这一测点，更准确地确定受热面的运行工况，所以笔者以锅炉低温过热器为例进行分析。

2 最小二乘支持向量机算法

设有n个训练样本(xi,yi)(i=1,2,…,n),x为n维训练样本输入,x∈Rn；yi为训练样本输出,yi∈R。决策函数f(x)=wTφ(x)+b。模型的数学描述为：

(3)

式中b——偏置量；

R——结构风险；

w——权值矢量；

γ——惩罚参数；

ξi——误差向量。

引入相应的Lagrange函数：

(4)

其中，α为Lagrange乘子，α=[α1,α2,…,αn]。

根据KKT条件，对式(4)求偏导得：

(5)

将求解的最优化问题转化为求解线性方程组，即：

(6)

其中，p=[φ(x1)Ty1,φ(x2)Ty2,…,φ(xn)Tyn]；q=[y1,y2,…,yn]；α=[α1,α2,…,αn]。

令

K(xi,xj)=<φ(xi),φ(xj)>

(7)

K(xi,xj)为核函数，根据泛函理论，满足Mercer条件的函数都可以作为核函数。

联立式(6)、(7)，得到LSSVM回归函数：

(8)

目前，常用的核函数主要有多项式核函数、径向基(RBF)核函数及神经网络核函数等。笔者选取径向基核函数：

(9)

3 模型建立和验证

3.1 参数选取

基于最小二乘支持向量机建立清洁吸热量模型的前提是，分析对流吸热面的清洁吸热量与锅炉的哪些运行工况参数有关。对流吸热面两侧分别为烟气侧和工质侧，可以将影响因素分为烟气侧和工质侧。烟气侧的直接影响因素是烟气量(一次风量、二次风量)、烟气温度(水平低温过热器入口烟温、给煤量和机组负荷)；工质侧的影响因素是工质的特性，主要包括工质流量、工质压力和工质入口温度。

3.2 样本准备

笔者以贵州黔西某电厂2#300MW燃煤机组为研究对象。该机组是哈尔滨锅炉厂生产的HG-1025/17.3-WM18型，为亚临界、自然循环、一次中间再热、双拱单炉膛、“W”火焰燃烧方式、尾部双烟道、烟气挡板调温、平衡通风、固态排渣、露天布置的全钢架悬吊煤汽包炉。锅炉燃料设计煤种、校核煤种均为黔西无烟煤。

笔者将长吹灰结束6～8min后的吸热面作为清洁吸热面，一般取20min的数据。选取2009年4月4～30日的数据，每隔5s取点，经过数据处理后，共得到15 913组数据，其中随机选取14 838组数据作为训练样本，剩余1 075组数据作为测试样本，部分数据见表1。

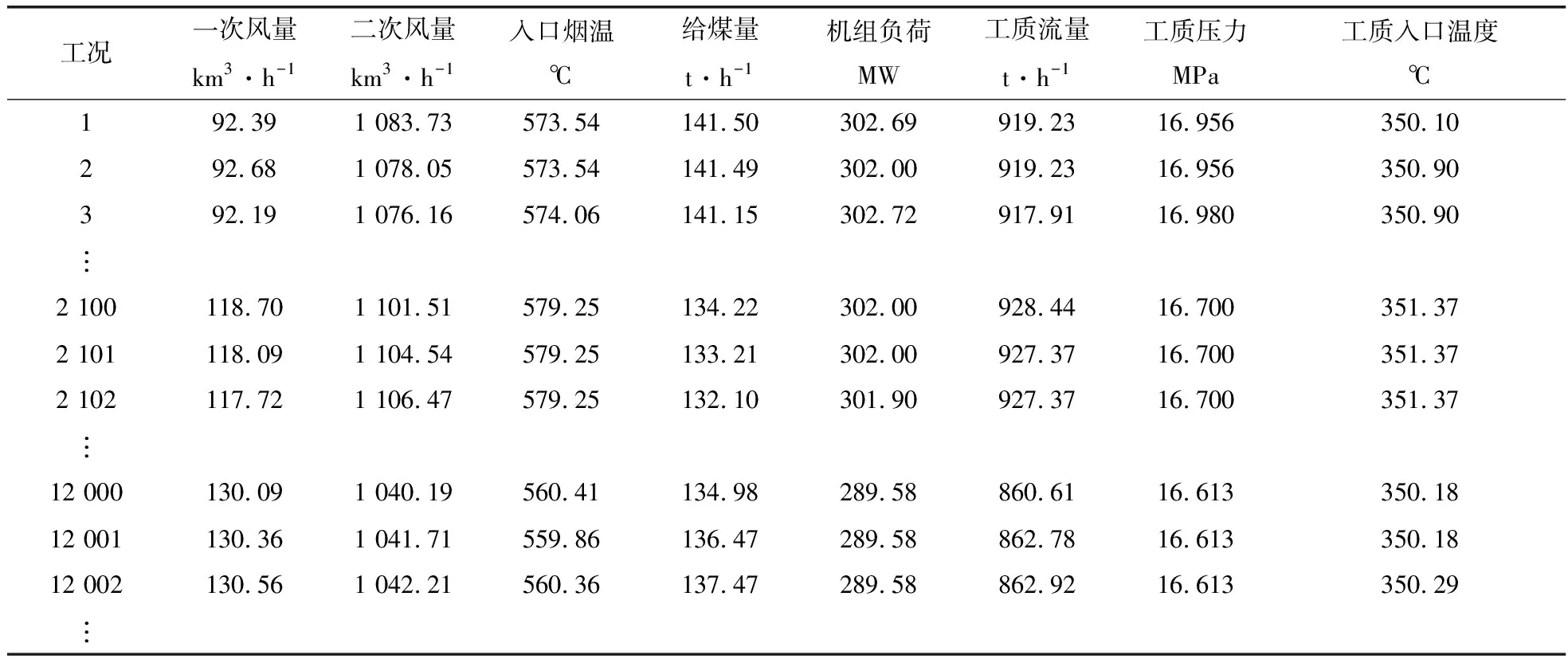
表1 热工数据

由于不同的热工参数单位不同，所以需要对采集到的数据进行归一化处理，将数据归一化到[0,1]区间。归一化公式为：

(10)

其中，x和x′分别是归一化前、后的值。

3.3 模型建立

LSSVM参数选择对模型的性能有很大的影响。笔者选取RBF核函数作为LSSVM算法的核函数，需要优化的参数是γ和σ，目前对参数的选取仍然没有统一的方法。

笔者采用粒子群算法对LSSVM的参数进行选择和优化。令种群群体规模N=20，迭代的最大次数kmax=100；LSSVM参数γ和σ的取值范围为γ∈[0,100000]，σ∈[0,100]。粒子群算法寻优流程如图1所示。

图1 粒子群算法对LSSVM的参数寻优流程

经粒子群算法寻优得到惩罚参数γ=56130，σ=0.47。

3.4 模型测试

表2列出模型对训练集和测试集的绝对误差和相对误差。模型的实际清洁吸热量和预测清洁吸热量的比较曲线如图2所示，模型的实际吸热量与预测吸热量的关系如图3所示。

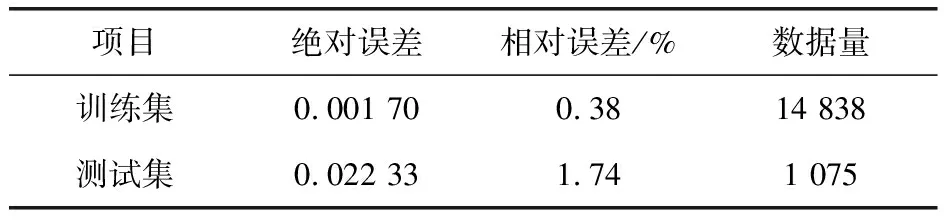
表2 LSSVM的预测精度

图2 模型对清洁吸热量的预测

图3 实际吸热量与预测吸热量的关系

从图2和表2中可以看出，基于LSSVM建立的低温过热器受热面清洁吸热量模型具有良好的预测性能。从表2可以看出，模型对训练样本的误差几乎是零，说明模型具有较好的逼近能力；对测试样本的误差也比较低，因此模型的预测性能较好。从图3可知，测试集的样本均匀地分布在参考线(斜率为1)两侧。

4 模型验证

模型应用中，笔者以贵州黔西某电厂2#300MW燃煤机组为研究对象，选取机组正常运行工况12h的数据，隔5s采样，经过数据处理后，得到热工参数共计8 000组样本，根据式(2)计算得到实际吸热量，再利用建立的模型预测出清洁吸热量，最后根据式(1)计算得到清洁系数K，绘制出低温过热器受热面积灰曲线，即清洁系数随时间的变化关系曲线，如图4所示。

图4 低温过热器受热面积灰曲线

由图4可知，随着锅炉的运行，受热面清洁系数逐渐下降，这主要是受热面不断积灰造成的。开始吹灰后，受热面开始变得清洁，清洁系数逐渐增大，当吹灰停止后，受热面又开始积灰，清洁系数又逐渐减小。

5 结束语

笔者基于最小二乘支持向量机和粒子群算法，对燃煤电站锅炉低温过热器受热面清洁吸热量进行建模，实现了对低温过热器受热面清洁吸热量的预测，从而能够对低温过热器的积灰状况进行有效的在线监测。以贵州黔西某电厂2#300MW燃煤机组为例，应用所建立的模型，得到了良好的效果。结果表明，以清洁系数来表征锅炉低温过热器的积灰情况具有可操作性，同时，最小二乘支持向量机和粒子群算法建立的模型具有良好的预测性能。在锅炉的运行过程中，模型得到的清洁系数有一定幅度的波动，这可能是由给煤量等锅炉热工参数造成的干扰，模型仍需要进一步改进。