基于相角裕度与鲁棒性解析法设计分数阶PIλ控制器

高学利 吕广芝

(烟台万华化工设计院有限公司，山东 烟台 264006)

随着现代工业的发展和工业过程控制精度的不断提高，对工业过程数学模型的建立提出了更高的要求，传统的整数阶模型不能达到精度要求，因为实际的工业过程控制中有许多系统都是分数阶系统。随着分数阶微积分理论的发展[1]，人们建立分数阶微分方程来描述实际分数阶系统，这样可以使模型更加精确。

由于PID控制器具有结构简单、鲁棒性强及易于操作等特点，被广泛地应用于工业过程控制中。对分数阶被控系统，用传统整数阶PID控制器来控制往往达不到理想的控制效果。当系统参数变化时，整个闭环系统控制效果变差甚至会不稳定，所以，针对分数阶被控系统，科学家们提出了分数阶控制器。由于分数阶PID控制器具有变量多、自由度高的特点，这给研究人员提供了更大的想象空间，并进行着不同方向的研究[2，3]。目前，分数阶控制理论已在工业过程控制中，特别是在冶金、化工、电力、轻工及机械等行业得到了广泛应用。笔者将介绍一种基于相角裕度与鲁棒性解析法设计的分数阶PIλ控制器。通过仿真对比常规PI控制器，表明设计的分数阶PIλ控制器具有更好的鲁棒性。

1 分数阶PIλ控制器①

传统的SISO闭环控制结构如图1所示。

其中被控对象G(s)的形式为：

(1)

图1 闭环控制系统

其中，L表示滞后时间，L>0；k表示被控对象增益；N(s)和D(s)是整数阶或者分数阶多项式；控制器C(s)为分数阶PIλ控制器，其形式为：

(2)

其中，kP是控制器的比例增益，TI是积分时间，分数阶积分阶次λ∈(0,2)。显然，控制器(2)比常规的PI控制器多一个可调节参数λ，从而提高了控制器的设计自由度，为额外的设计要求提供了可能。

笔者的目的是提供一种简单的解析法，设计分数阶PIλ控制器使系统得到期望的相角裕度，且当被控对象的增益发生变化时，系统阶跃响应变化不大，从而使系统有更好的鲁棒性。

2 分数阶PIλ控制器设计

首先，考虑开环控制系统G(s)C(s)在幅值穿越频率ωc处的相角裕度，满足下列方程：

=-π+φm

(3)

其中φm为期望的开环系统相角裕度，A(ωc)=∠G(jωc)。众所周知，系统的相角裕度直接影响系统阶跃响应的超调量。

由式(3)推出：

(4)

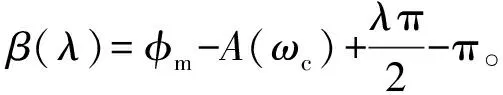
为使系统增益发生变化时，系统有较好的鲁棒性，引入如下方程：

(5)

该设计的目的是使系统的伯德图在幅值穿越频率处变化平缓，这意味着当系统增益发生变化时，系统的阶跃响应超调量变化不大，从而使控制系统具有较强的鲁棒性。

由式(5)可推出：

(6)

其中：

综上所述，分数阶PIλ控制器设计需要确定3个参数λ、kp和TI，而两个方程(4)和(6)不能确定3个未知数。因此，附加最后一个方程：

|C(jωc)G(jωc)|=1

(7)

从式(7)推出：

(8)

其中,C(ωc)=|G(jωc)|。

由式(4)可得：

(9)

将式(9)代入式(6)得到：

(10)

给定截止频率ωc，非线性方程(10)的唯一未知量λ可用图解法解得。

由式(9)可推出：

(11)

根据式(8)可得到：

(12)

3 仿真研究

本章中仿真研究的被控制对象为整数阶时滞被控对象和分数阶时滞被控对象。

例1 一阶时滞系统

(13)

这类传递函数是由许多工业生产过程中的S形响应曲线逼近出来的。假设k=5，T=10，L=0.4。根据解析法设计分数阶PIλ控制器。给定期望的相角裕度φm=π/4，截止频率ωc=0.9。利用上述方法依次求得λ=1.06，TI=3.71，kP=1.26。

为显示分数阶PIλ控制器的优越性，对比常规的PI控制器。

(14)

利用著名的Ziegler-Nichols整定规则整定PI控制器的参数。四分之一衰减曲线法得到TI=1.33，kP=4.5。

根据上述结果，分别做出PIλ控制系统和常规PI控制系统的开环伯德图，如图2所示。

图2 开环伯德图

从图2中可以看出，在幅值穿越频率ωc处，通过解析法得到的PIλ控制系统的相角裕度曲线变化平缓，而通过Z-N方法整定得到的常规PI控制系统相角裕度变化很大。因此可以推得，依照传统的Z-N整定方法得到的PI控制器的鲁棒性比笔者提出的通过解析法得到分数阶PIλ控制器的差。

当开环控制系统增益在±20%之间变化时，分别绘出分数阶PIλ控制器与常规PI控制器控制下系统的阶跃响应曲线(图3)。

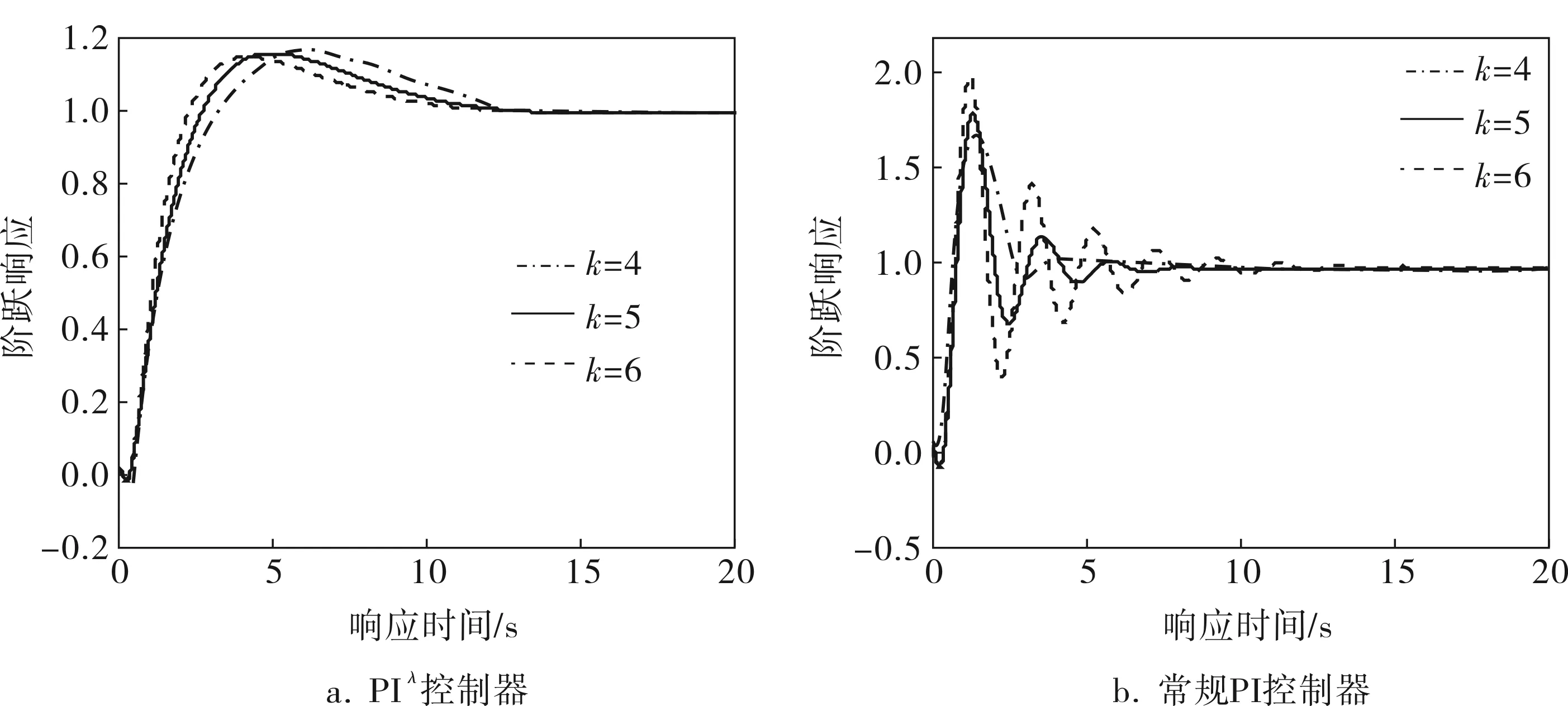
图3 阶跃响应曲线

仿真结果表明，当被控对象的增益变化时，通过解析法设计的分数阶PIλ控制器能使系统达到期望的鲁棒性，而常规PI控制器的控制效果不好。

例2 分数阶被控对象

(15)

这是一个普通的膜式电容器的分数阶模型，在描述细胞膜、细胞、组织和大量的生物组织方面有着非常重要的意义。假设T=0.4，k=1，α=1.4，接下来设计相应的分数阶PIλ控制器。给定期望的相角裕度为φm=π/3，幅值穿越频率ωc=0.5。由上述方法可求出3个参变量的值分别为λ=0.72，TI=2.89，kP=0.31。

当系统的增益在0.8～1.2(标量±20%)变化时，分别绘出各自的闭环阶跃响应曲线(图4)。显然，用解析法设计的分数阶控制器控制这种类型的分数阶被控对象，能使系统有较强的鲁棒性。

4 结束语

由于分数阶微积分环节所固有的一些特性，其可以更加真实地反映实际系统的渐近变化情况，且引入的积分、微分阶次能增加模型设计的灵活度。虽然分数阶系统的离散化数字实现仍然相对困难，实施结果相对复杂，但随着计算技术的高速发展，在自动控制理论工程实际应用中分数阶微积分理论必将有着越来越广泛的应用。

图4 阶跃响应曲线