随机环境中可迁移两性分枝过程的极限性质

宋明珠，胡守鹏

(铜陵学院数学与计算机学院，安徽 铜陵 241000)

随机环境中可迁移两性分枝过程的极限性质

宋明珠，胡守鹏

(铜陵学院数学与计算机学院，安徽 铜陵 241000)

在独立同分布的随机环境下，建立了随机环境中可迁移的两性分枝过程{Zn}n≥0，且迁移人口数依赖当前人口数.证得{Zn}n≥0和{(Fn，Mn)}n≥0是随机环境中的马氏链，并得到了第n代每个配对单元平均增长率{rk}k>0的极限性质，从而推广了经典两性分枝过程的相关理论.

随机环境；两性分枝过程；迁移依赖人口数；马氏链；极限性质

1 预备知识

为了更精确地描述某种生物的人口模型，D.J.Daley在1968年首次引入了两性分枝过程的模型，得到众多概率论学者的广泛关注和深入地研究[1-8].由于自然界生物在繁衍的过程受到自然环境、社会环境等诸多因素的影响，作为两性分枝过程和随机环境中分枝过程的自然推广，马世霞引入了随机环境中的两性分枝过程，得到了一系列有价值的结果[6-7].实际上生物为了生存，有些个体需要离开原来的群体，同样也有新的个体加入到这个群体中来，即生物人口的迁移.现在大多数模型只考虑各类环境对配对数目的影响，而忽视人口迁移对配对数目的影响.本文从环境和人口迁移两方面出发，建立了随机环境中可迁移的两性分枝过程，且迁移人口数依赖当前人口数，推导出这类两性分枝过程是随机环境中的马氏链，以及第n代每个配对单元平均增长率的极限性质，进而推广了经典两性分枝过程的相关理论.

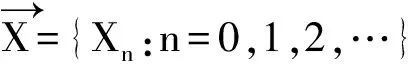
定义1.1 若{Zn}n≥0满足：

(1)Z0=N∈N+；

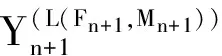
定义1.2 如果对任意的x，n∈N+，有

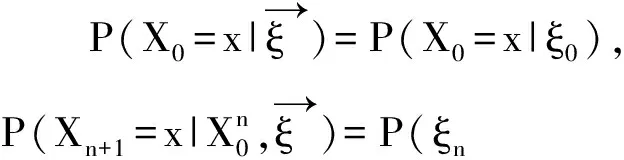
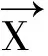
记

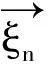
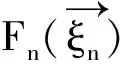
2 马氏性

定理2.1 {Zn}n≥0是随机环境中的马氏链，其一步转移概率为

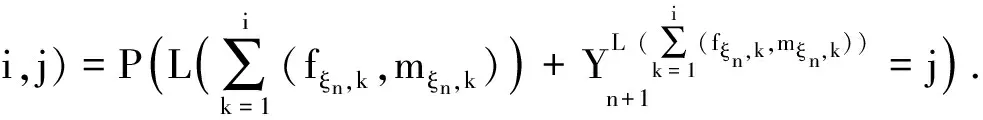
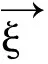
由定义1.2知{Zn}n≥0是随机环境中的马氏链.

定理2.2 {(Fn，Mn)}n≥1中随机环境中的马氏双链，其一步转移概率为

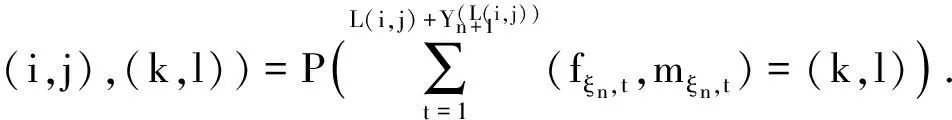
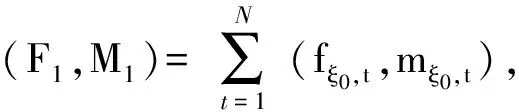
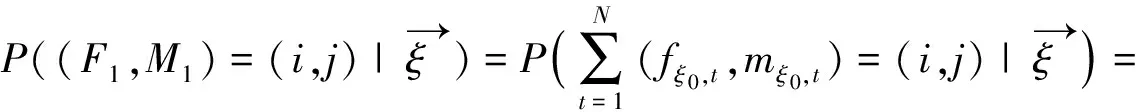
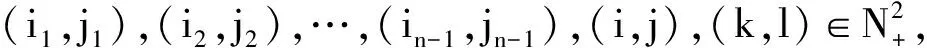
由定义1.2知{(Fn，Mn)}n≥1是随机环境中的马氏链.

3 极限性质

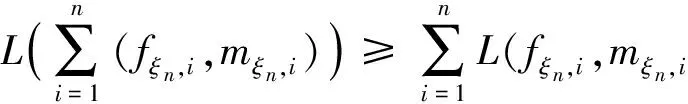
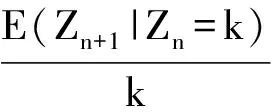
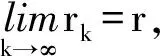
第一步 因为{(fξn，i，mξn，i)}i=1，2，…独立同分布，由强大数定理得

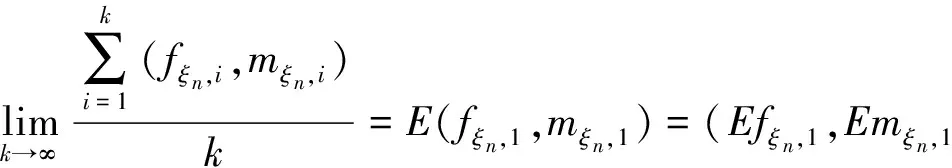
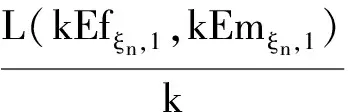
因为配对函数L(·，·)是上可加性的且非负的，所以

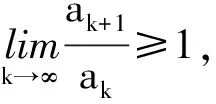
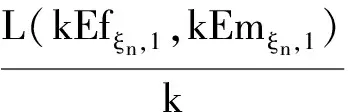
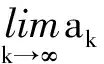
第三步 证明r(·，·)是二元连续函数.

由r(Efξn，1，Emξn，1)的定义和L(x，y)对每个分量单调不减，对任意的ε

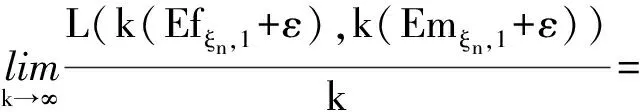
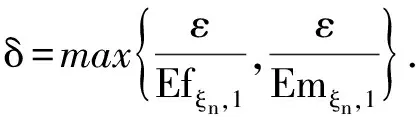
同理可得

r(Efξn，1-ε，Emξn，1-ε)≥(1-δ)r(Efξn，1，Emξn，1).

从而令ε↓0，则δ↓0，所以

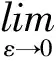
(1)

又因为

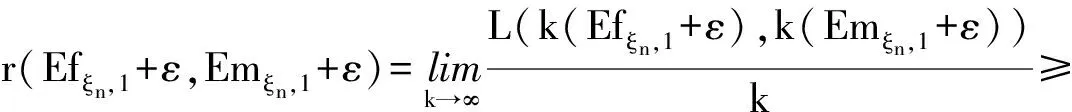
(2)

由(1)和(2)式可得

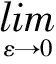
所以r(·，·)是二元连续函数.

由第一步可知

所以∀ε，∃k0，∀k>k0有

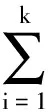
又因为配对函数L(·，·)是上可加的，所以有

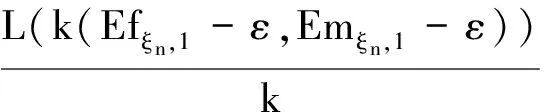
令k→∞，得

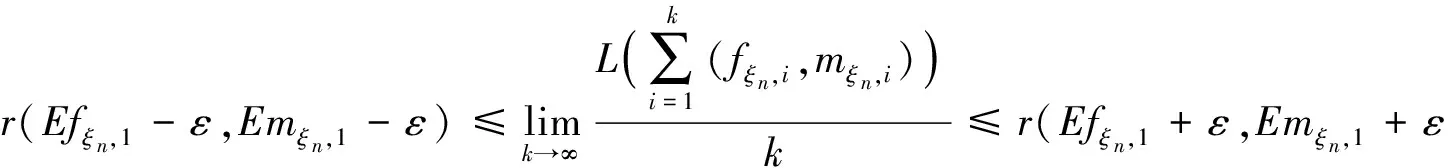
再令ε→0，由r(·，·)是二元连续函数，得

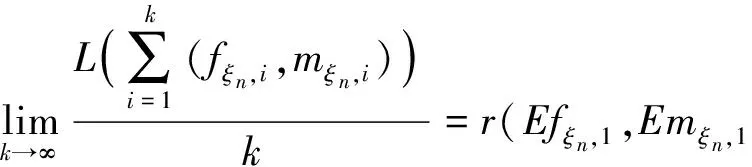
因为L(x，y)≤x+y，所以

由强大数定理可知

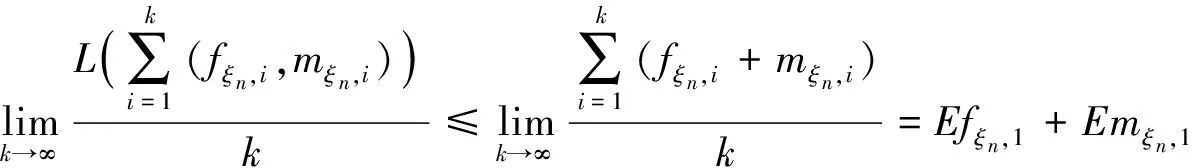
所以当k充分大时，

由控制定理可知，期望和取极限可交换次序，即

(3)

(4)

由(3)式和(4)式知

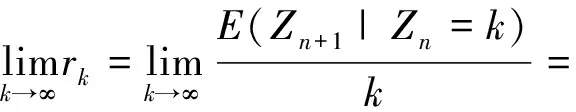
即定理3.1得证.

注 由定理3.1的证明过程可知，只要迁移的配对数有限，则随机环境中可迁移两性分枝过程的第n代每个配对单元平均增长率的极限值，与随机环境中两性分枝过程第n代每个配对单元平均增长率的极限值相等，从而推广了经典随机环境中两性分枝过程的相关结论.

又因为EL(fξ0，1，mξ0，1)>0，故存在正整数i，j，使pi，j(ξ0)>0.不失一般性，设

k1=L(k0(i，j))+k0，k2=L(k1(i，j))+k0，…，kn+1=L(kn(i，j))+k0，…

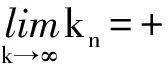
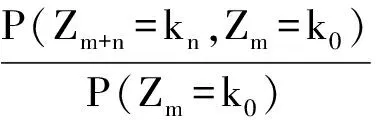
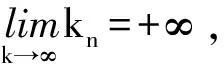
[1] DALEY D J.Extinction conditions for certain bisexual Galtion-Waston processes[J].Z Wahr，1968，9(2)：315-322.

[2] SMITH W L，WILKINSON W E.On branching processes in random environments[J].Ann Math Statist，1969，40(3)：814-827.

[3] MOLINA M，MOTA M，RAMOS A.Bisexual Galton-Waston lranching processes with population-size-depengent mation[J].J Appl Prob，2002，39：479-490.

[4] MOLINA M，MOTA M，RAMOS A.Bisexual Galton-Waston branching processes in varying envirnments[J].Stoch Anal Appl，2003，21：1353-1367.

[5] 邢艳春.一阶马氏下潜变量模型的多元纵向数据分析[J].东北师大学报：自然科学版，2013，45(3)：46-50.

[6] SHI-XIA MA.Bisexual Galton-Waston branching processes in random environments[J].Acta Mathematicae Applicatae Sinica：English Series，2006，22(3)：419-428.

[7] 马世霞.随机环境中两性Galton-Waston分枝过程[J].河北工业大学学报，2008，37(1)：68-72.

[8] 沈燕，王学军，胡舒合.NOD随机阵列加权和的完全收敛性[J].东北师大学报：自然科学版，2012，44(4)：1-5.

(责任编辑：陶 理)

The limit properties of the bisexual branching process with population-size-dependent migration in random environments

SONG Ming-zhu，HU Shou-peng

(College of Mathematics and Computer Science，Tongling University，Tongling 241000，China)

In this paper，we consider a bisexual branching process with population-size-dependent migration in independent and identically distributed random environments.It is proved the bisexual branching process is Markov chains in random environments and the double chains about the number of females and males in the nth generation is double Markov chains in random environments，too.The limit properties of the mean growth rate per mating unit is studied.Some limit properties known about classical bisexual branching process in random environments are enlarged.

random environments；bisexual branching process；population-size-dependent migration；Markov chains；limit properties

1000-1832(2014)04-0009-06

10.11672/dbsdzk2014-04-002

2013-06-08

安徽省自然科学基金资助项目(1308085MA03)；安徽高校省级自然科学研究项目(kj2013z331).

宋明珠(1979—)，女，硕士，主要从事随机环境中的马氏链研究.

O 211.65 [学科代码] 110·64

A