Hilbert K-模上酉系统的广义框架向量集的参数化

董 芳 芳

(天水师范学院数学与统计学院，甘肃 天水 741001)

HilbertK-模上酉系统的广义框架向量集的参数化

董 芳 芳

(天水师范学院数学与统计学院，甘肃 天水 741001)

引入了紧算子代数模(简称HilbertK-模)上广义框架，广义框架算子，酉系统以及其广义框架向量集的概念，研究了其性质，最后得到了广义框架向量集的参数化定理.

HilbertK-模；广义框架；酉系统；广义框架向量集；参数化

1 Hilbert K-模及框架

HilbertK-模是一种特殊的HilbertC*-模，其中K为作用在Hilbert空间上的全体紧算子组成的C*-代数，显然I∉K，且D.Bakic和B.Guljas在文献[1]中证明了这种模一定有特殊的标准正交基，其特殊点在于相同标准正交基向量的内积为K中的一个秩1的自伴投影.

定义1.1[1]设K为作用在Hilbert空间H上的全体紧算子组成的C*-代数，M是复数域C上的线性空间，M是左K-模，满足μ(kx)=(μk)x=k(μx)，∀μ∈C，∀k∈K，∀x∈M，若〈，〉:M×M→K具有性质:

(ⅰ) 〈x，x〉≥0，∀x∈M；

(ⅱ) 〈x，x〉=0⟺x=0，∀x∈M；

(ⅲ) 〈x，y〉=〈y，x〉*，∀x，y∈M；

(ⅳ) 〈kx，y〉=k〈x，y〉，∀k∈K，∀x，y∈M；

(ⅴ) 〈x+y，z〉=〈x，z〉+〈y，z〉，∀x，y，z∈M.

则称(M，〈，〉)为准HilbertK-模.在M上定义范数‖x‖∶=‖〈x，x〉‖1/2，若M在该‖·‖意义下完备，就称之为HilbertK-模.

定义1.2[1]称序列{vλ，λ∈Λ}为HilbertK-模M的标准正交序列，若∀λ，μ∈Λ，

其中ξ∈H，且‖ξ‖=1 (H为Hilbert空间)，eξ，ξ∈K，K：∀η∈H，eξ，ξ(η)=(η，ξ)ξ.

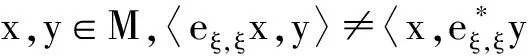
定义1.3[2]称HilbertK-模M中的序列{xλ，λ∈Λ}为框架，若存在常数c>0，d>0，使得∀x∈M，

若c=d=1，则称{xλ，λ∈Λ}为正规紧框架；若只有右半部等式成立，则称{xλ，λ∈Λ}为Bessel序列.

定义1.4[2]设M1，M2均为HilbertK-模，T:M1→M2是K-线性算子(即T(kx)=kT(x)，∀x∈M1，∀k∈K)，若存在K-线性算子T*:M2→M1，使得∀x∈M1，∀y∈M2，〈Tx，y〉=〈x，T*y〉，则称T是可伴算子.

定义1.5[2]设T为M1到M2的可伴算子.若T为双射，即T既为单射，也为满射，则称T为可逆算子；若T*T=TT*=I，则称T为酉算子.

2 Hilbert K-模上的广义框架

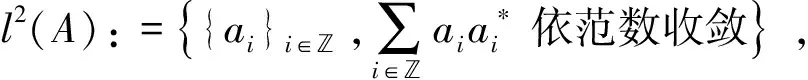
而对HilbertK-模，由于I∉K，也就是HilbertK-模无法膨胀，即引入

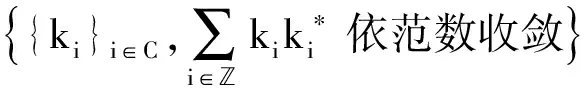
是没有意义的，因此，在以往的研究中，只能在K-模M自身上引入算子θ:M→M，使得∀x∈M，

其中{vλ，λ∈Λ}为M的标准正交基，则θ是有闭值域且可伴的算子，

且

θ*(vλ)=eξ，ξxλ.

受这点的启发，我们考虑HilbertK-模M，Nj，j∈J，其中J为有限或可数生成的指标集，并且在M到Nj上引入类似于θ的算子列Aj:M→Nj，使得

其中{xj，λ，λ∈Λ}为M的框架，{vj，λ，λ∈Λ}为Nj的标准正交基，同时Aj为可伴算子，且

我们将{eξ，ξxj，λ，j∈J，λ∈Λ}称为算子序列{Aj，j∈J}的诱导系列，这样研究的核心就从K-模M上的序列{xλ，λ∈Λ}的研究上升到算子序列{Aj，j∈J}的研究.

由{Aj，j∈J}的引入，显然有

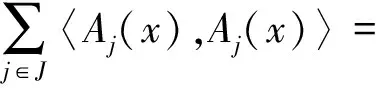
这样如何把算子序列{Aj，j∈J}定义为框架、Bessel序列、正规紧框架，自然就与HilbertK-模上序列{xλ，λ∈Λ}定义为框架、Bessel序列、正规紧框架的定义方法联系起来，为了区别起见，这里称为广义框架、广义Bessel序列、广义正规紧框架，并且和孙文昌在2005年引入的Hilbert空间上的g-框架的概念相类似.[3-6]

下面我们给出HilbertK-模上的广义框架的定义.

定义2.1 设M，Nj均为HilbertK-模，Aj:M→Nj，称该算子序列{Aj，j∈J}为M关于Nj的广义框架，若存在A>0，B>0，使得∀x∈M，有

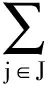
特别的，若A=B=1，则称{Aj，j∈J}为M关于Nj的广义正规紧框架，将a，b分别称为其广义下、上框架界；若只有右半不等式成立，则称{Aj，j∈J}为M关于Nj的广义Bessel序列.

定义2.2[2]称序列{Λj，j∈J}为M关于Nj的广义标准正交基，若满足：

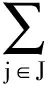
3 Hilbert K-模上广义框架的框架变换

由于在HilbertK-模M上，l2(K)不存在，也就是将M膨胀没有意义，从而我们在M本身引入广义框架{Aj，j∈J}的框架变换.

根据定义我们易知Φ为单射.事实上，由于{Aj，j∈J}为广义框架，从而存在a，b>0，使得

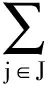
即

a〈x，x〉≤〈Φ(x)，Φ(x)〉≤b〈x，x〉.

事实上，∀x∈M，

性质3.1 设{Aj，j∈J}为M关于Nj的广义框架，S为{Aj，j∈J}的广义框架算子，则∀x∈M，

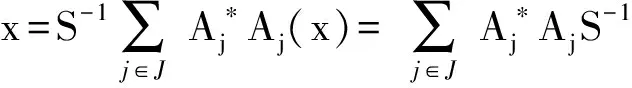
即

4 Hilbert K-模上的酉系统及广义框架向量集的参数化

定义4.1 HilbertK-模M上的酉系统U是指L(M)中的全体酉算子的子集，且I∈L(M)，由M上的全体酉算子组成的半群称为酉半群(对结合律封闭)，组成的群称为酉群.

定义4.2 称M关于Nj的序列{Aj，j∈J}为酉系统U的完全游荡广义框架向量集，若{Aju，j∈J，u∈U}为M关于Nj的广义标准正交基；称{Aj，j∈J}为U的(正规紧)广义框架向量集，若{Aju，j∈J，u∈U}为M关于Nj的(正规紧)广义框架；称{Aj，j∈J}为U的广义Bessel向量集，{Aju，j∈J，u∈U}为M关于Nj的广义Bessel序列.

注 {Aju，j∈J，u∈U}为M关于Nj的广义标准正交基具体为：

同时，(1)也等价于

定义4.3 设{Aj，j∈J}为U的某广义序列.称CAj(U)∶={t∈L(M)，Aj(tu-ut)=0，∀j∈J，∀u∈U}为U在{Aj，j∈J}处的局部换位；称U′∶={t∈L(M)，tu=ut，∀u∈U}为U的换位.

定理4.1 设U为作用在M上的酉半群，{Aj，j∈J}为U的广义框架向量集，S为{Aju，j∈J，u∈U}的广义框架算子，则S∈U′.

证明 由性质3.1，

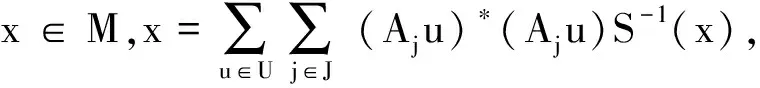
用S(x)代替x，有

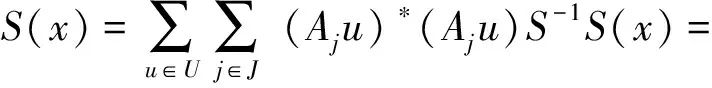
从而∀v∈V，

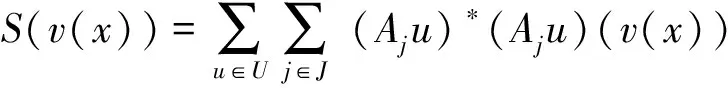
而另一方面，若v∈U，则v*∈U，由于U为酉半群，从而，若v*∈U，u∈U，则uv*∈U，因此，∀v∈V，

即S∈U′.

定理4.2 设U为作用在M上的酉半群，{Aj，j∈J}为U的某完全游荡广义框架向量集，则：

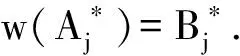
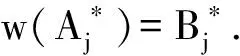
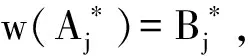
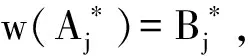
证明 我们引入算子w:M→M，使得∀x∈M，

则w是定义好的，且w为可伴算子，

同时w∈U′.

事实上，由于U为酉半群，从而对u，v∈U，uv∈U，有v*∈U，uv*∈U，于是，∀v∈U，

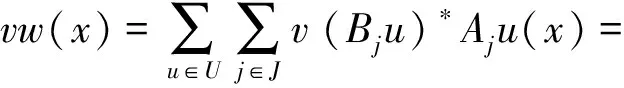
即w∈U′.

又由于{Aju，j∈J，u∈U}为M关于Nj的广义标准正交基，从而∀v∈U，当然v*∈U，及∀j∈J，

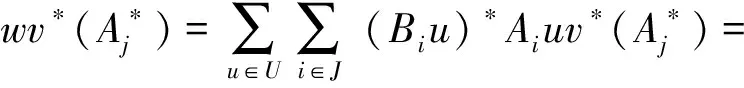
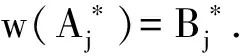
下面我们证明在不同的条件下，w所具有的性质.

(1) 由于{Aj，j∈J}和{Bj，j∈J}均为U的完全游荡广义框架向量集，则

且

即

也有一样的性质.于是，∀x∈M，

即w*w=I.同理，

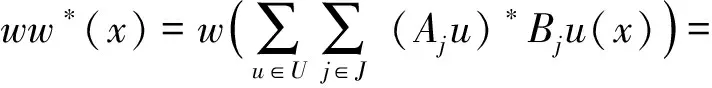
即ww*=I，因此w*w=ww*=I，即w为酉算子，也即w为可逆算子.

(2) 当{Bj，j∈J}为U的正规紧广义框架向量集时，即∀x∈M，

也即

结合{Aj，j∈J}均为U的完全游荡广义框架向量集及(1)的证明过程知：ww*=I，即w为余等距算子.

(3) 当{Bj，j∈J}为U的广义框架向量集时，存在a，b>0，使得∀x∈M，

即

结合(1)的证明过程知，

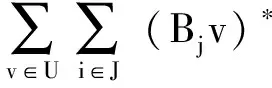
即

aI≤ww*≤bI.

(4) 该结论的证明可由(3)的证明过程得到，这里不再赘述.

[1] BAKICD，GULJAS B. HilbertC*-modules overC*-algebras of compact operators [J]. Acta Sci Math：Szeged，2002，68：249-269.

[2] FRANK M，LARSON D R. Frames in HilbertC*-modules andC*-algebras [J]. Operator Theory，2002(48)：203-233.

[3] SUN W C. G-frames andg-Riesz Bases [J]. Math Anal Appl，2006，322(1)：437-452.

[4] 任美英.一类推广的Bernstein算子的逼近[J]. 东北师大学报：自然科学版，2013，45(3)：30-34.

[5] COO M，LAMMERS M C. A HilbertC*-modules for Gabor systems [J]. Math FA，2001(20)：1-13.

[6] HAN D G，LARSON D R. Bases and group representations [J]. Memoirs，Amer Math Soc，2000，147(697)：46-50.

(责任编辑：陶 理)

The parameterization of generalized frame vector set for unitary system on HilbertK-modules

DONG Fang-fang

(College of Mathematical and Statistics，Tianshui Normal University，Tianshui 741001，China)

In this paper，the concepts of generalized frames，generalized frame operator，unitary system on HilbertK-module and its generalized frame vector set are introduced and their properties are studied.Finally，the theory of parameterization of generalized frame vector set for unitary system on HilbertK-module are obtained.

HilbertK-module；generalized frames；unitary system；generalized frame vector set；parameterization

1000-1832(2014)04-0036-06

10.11672/dbsdzk2014-04-006

2013-05-05

国家自然科学基金资助项目(10771101)；天水师范学院中青年教师科研基金资助项目(TSY201201).

董芳芳(1981—)，硕士，讲师，主要从事泛函分析研究.

O 177.1 [学科代码] 110·5725

A